题目要求
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。 叶子节点 是指没有子节点的节点。- 示例 1:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。 - 示例 2:
输入:root = [1,2,3], targetSum = 5
输出:false
解释:树中存在两条根节点到叶子节点的路径:
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。 - 示例 3:
输入:root = [], targetSum = 0
输出:false
解释:由于树是空的,所以不存在根节点到叶子节点的路径。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/path-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
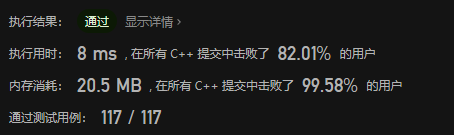
解法
递归
先将问题简化,看看最简单的情况:
树为空,即根节点为空,那么自然返回false;
树只有根节点,即根节点的左右子树全为空,那么就判断根节点的值和目标值是否相等即可;
再进一步,根节点的左右子树不为空,那么就分别去找左右子树,看看其值是否等于目标值减去根节点所得到的值。
依照这个思路得出:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if (root == nullptr)
{
return false;
}
if (root->left == nullptr && root->right == nullptr)
{
return targetSum == root->val;
}
return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val);
}
};
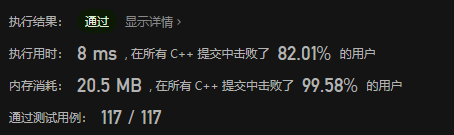
复杂度分析
时间复杂度:
O
(
n
)
O(n)
O(n)
空间复杂度:开辟辅助数组所出现的消耗,
O
(
h
)
O(h)
O(h)
