6126:
题目:
设有一个售货员从城市1出发,到城市2,3,…,n去推销货物,最后回到城市1.假定任意两个城市i,j间的距离dij(dij=dji)是已知的,问他应沿着什么样的路线走,才能使走过的路线最短?
输入:
第1行城市个数n
从第2行开始输入任意两个城市之间距离的矩阵,没有道路的两个城市之间的距离为-1
输出:
第1行:最短距离
第2行:城市顺序
输入输出实例:
输入:
4? ? ? //城市个数
-1 30 6 4? ? ? ? ?//城市之间距离矩阵
30 -1 5 10
6 5 -1 20
4 10 20 -1
输出:
25? ? //最短距离
1 3 2 4? ? //
思考在代码段里面了
#include <iostream> using namespace std; const int N = 10; int g[N][N], x[N]; int best[N], ans, cost; // best[] 记录 最终 的最短路线 ,ans 最小距离值 // x[] 记录 在 dfs 过程中的 可能行走的路线 ,cost 对应路线的 距离值 int n; void dfs(int t) { if (t > n) //到达叶子结点 { if (g[x[t - 1]][1] > 0 && cost + g[x[t - 1]][1] < ans) { ans = cost + g[x[t - 1]][1]; for (int i = 1; i <= n; i++) best[i] = x[i]; } return; } else { for (int i = t; i <= n; i++) { if (g[x[t - 1]][x[i]] > 0 && g[x[t - 1]][x[i]] + cost < ans) { cost += g[x[t - 1]][x[i]]; swap(x[t], x[i]); //保存要去的第t个城市到x[t]中,即x[i] 为要去的 第t个城市//第一个城市 dfs(t + 1); //搜索下一个城市 // 回溯 cost -= g[x[t - 1]][x[t]]; swap(x[t], x[i]); } } } } int main() { cin >> n; for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) { cin >> g[i][j]; } ans = 10000; //无穷大量 cost = 0; for (int i = 1; i <= n; i++) { x[i] = i; } dfs(2); cout << ans << endl; for (int i = 1; i <= n; i++) { cout << best[i] << " "; } return 0; }
?6125:
题目:
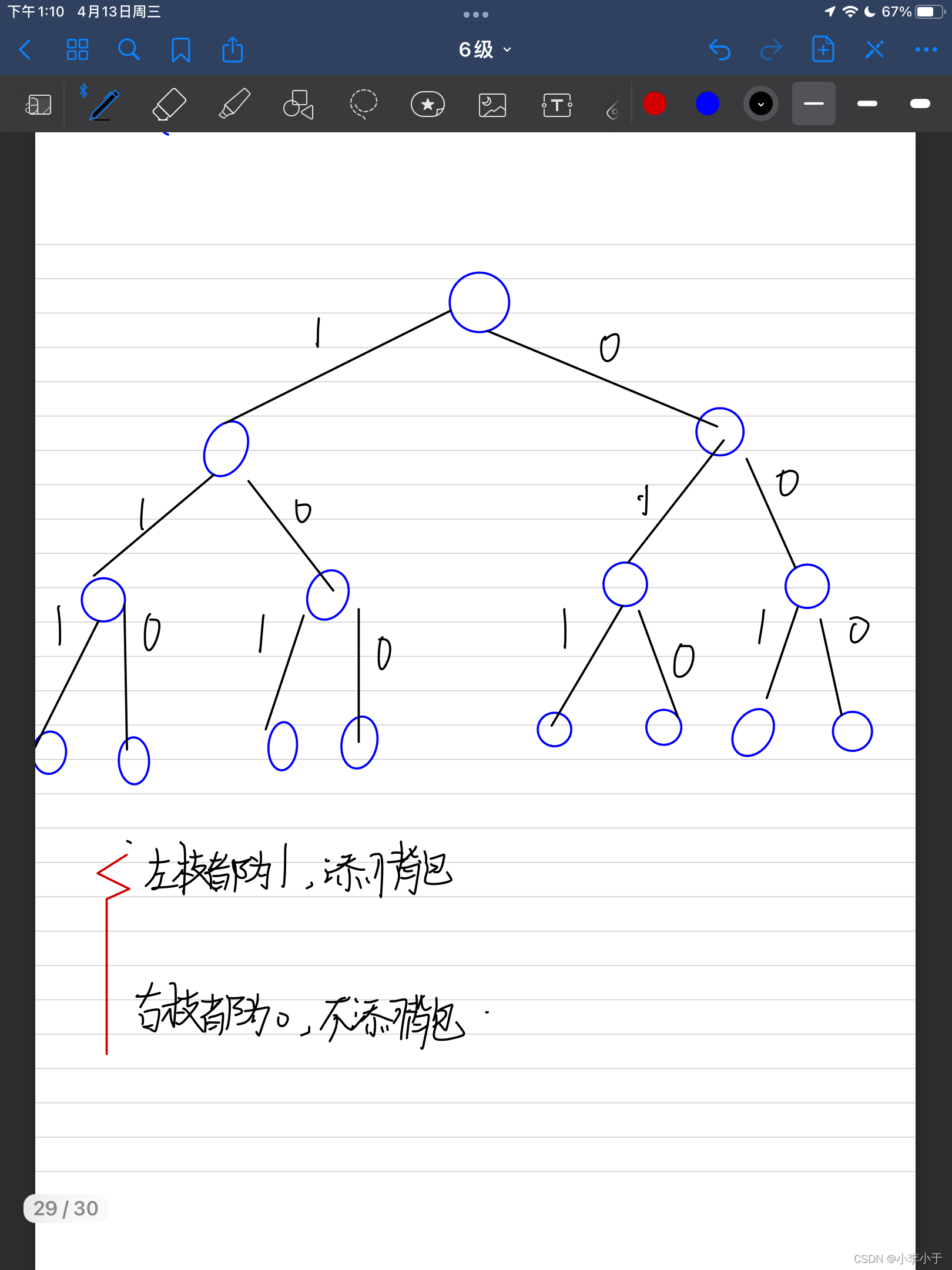
有n件物品和一个容量为c的背包。第i件物品的价值是v[i],重量是w[i]。求解将哪些物品装入背包可使价值总和最大。所谓01背包,表示每一个物品只有一个,要么装入,要么不装入。
输入:
第1行是背包容量
第2行物品个数n
第3行:n个物品的重量
第4行:n个物品的价值
输出:
第1行:最优值
第2行:最优解
输入输出范例:
输入:
50? ?//背包容量
4? ?//物品个数
30 20 40 10? ? //物品重量
10 20 30 40? ? //物品价值
输出:
70? ? //最优值
0 0 1 1? ? //最优解
理解:对子集树的理解
?
?
#include<iostream> using namespace std; int n, t;//n是物品个数 double C;//背包容量 double w[105];//重量 double v[105];//价值 double p[105];//物品单位价值 int BestX[105];//最合适的序号合适为1不合适为0 int X[105];//现阶段最合适的序号 int order[100];//记录下那个序号在knapsack的时候进行过交换 double CurWeight = 0.0;//现阶段背包物品的重量 double CurValue = 0.0;//现阶段背包物品的价值 double BestValue = 0.0;//背包物品的最大价值 void knapsack()//将物品按照单位重量价值排序; { int temporder = 0; double temp = 0.0; for (int i = 1; i <= n; i++) p[i] = v[i] / w[i];//物品价值/物品重量 for (int i = 1; i <= n - 1; i++) { for (int j = i + 1; j <= n; j++) if (p[i] < p[j]) { temp = p[i]; p[i] = p[j]; p[j] = temp; temporder = order[i]; order[i] = order[j]; order[j] = temporder; temp = v[i]; v[i] = v[j]; v[j] = temp; temp = w[i]; w[i] = w[j]; w[j] = temp; } }//将物品按照单位重量价值排序; } int bound(int t) { int cleft = C - CurWeight;//剩余容量 int b = CurValue;//现阶段背包内物品的价值 while (t <= n && w[t] <= cleft)//以物品重量价值递减装入物品 { cleft = cleft - w[t]; b = b + v[t]; t++; } if (t <= n)//装满背包 b = b + v[t] * cleft / w[t];//计算t号物品的单位价值装满剩余空间 return b; } void backtrack(int t) { if (t > n)//到达叶子节点了 { if (CurValue > BestValue)//已经搜寻完一次了,把现有的最大值赋值; { BestValue = CurValue; for (int i = 1; i <= n; i++) BestX[i] = X[i]; } return; } if (CurWeight + w[t] <= C)//不到背包最大容量进入左子树 { X[t] = 1;//记录是否装入 CurWeight += w[t]; CurValue += v[t]; backtrack(t + 1);//回溯 CurWeight -= w[t]; CurValue -= v[t]; } if (bound(t + 1) > BestValue)//进入右子树 { X[t] = 0;//他自己没有后面物品合适 backtrack(t + 1);//判断 } } int main() { cin >> C >> n; //背包容量和物品个数 for (int i = 1; i <= n; i++)//都是从一开始的 { cin >> w[i]; //物品重量 order[i] = i;//序列号的意思 } for (int i = 1; i <= n; i++) cin >> v[i];//物品价值 knapsack(); backtrack(1); cout<<BestValue<<endl; for (int i = 1; i <= n - 1; i++) { for (int j = 1; j <= n - 1; j++) { if (order[j] > order[j + 1]) { t = order[j]; order[j] = order[j + 1]; order[j + 1] = t; t = BestX[j]; BestX[j] = BestX[j + 1]; BestX[j + 1] = t; } } }//他要求输出的是原来的序号 for (int i = 1; i <= n; i++) cout<<BestX[i]; return 0; }