[数据结构与算法]算法 ：快速排序详解 | 递归与非递归形式 | 优化方案 | 单向划分如何编写？

前言

实际上快速排序用到的思想也是分治策略，将问题的规模缩小，本质不变。
在之前的文章中，有写过快速排序的递归写法，重点就是Partition函数。
本文接着对分治策略进行讲解。

【快速排序（递归方式）】

如果了解递归做法，可根据目录跳过回归部分。若想了解，可点上方文章，对划分函数有详细注释。

一、回顾递归形式

1.Partition函数

原理：
每次找到基准值，以基准值为分界线，左边的值全部比基准值小，右边的值全部比基准值大。

规则：

1. 从右向左找比基准值小的数据，找到后放到左边；
2. 从左向右找比基准值大的数据，找到后放到右边；
3. 重复 1、2操作，如果 left == right （下标），循环退出，再将基准值放到nums[left]或nums[right]。

代码：

int Partition(int* nums, int left, int right)
{
	int key = nums[left];
	while (left < right)
	{
		while (left < right && nums[right] > key)
		{
			--right;
		}
		if (left < right) nums[left] = nums[right];

		while (left < right && nums[left] <= key)
		{
			++left;
		}
		if (left < right) nums[right] = nums[left];
	}
	nums[left] = key;

	return left;
}

通过主要的划分函数，其他代码就很好写：

void PassQuick(int* nums, int left, int right)
{
	if (left < right)
	{
		int pos = Partition(nums, left, right);

		PassQuick(nums, left, pos - 1);
		PassQuick(nums, pos + 1, right);
	}
}
void QuickSort(int* nums, int numsSize)
{
	if (nums == nullptr || numsSize <= 1) return;

	PassQuick(nums, 0, numsSize - 1);
}

2.测试用例

void PrintNums(const int* nums, int numsSize)
{
	if (nums == nullptr || numsSize < 0) return;
	for (int i = 0; i < numsSize; ++i)
	{
		cout << nums[i] << "  ";
	}
	cout << endl;
}

int main(void)
{
	int nums[] = { 52, 12, 78, 90, 34, 23, 100, 56, 45, 67, 89 };
	int numsSize = sizeof(nums) / sizeof(nums[0]);
	PrintNums(nums, numsSize);
	QuickSort(nums, numsSize);
	PrintNums(nums, numsSize);

	return 0;
}

二、非递归形式

如果面试时让手写快排，写出了递归形式，面试官再问非递归形式，这个就必须得会。。。

1. 引入队列queue

非递归形式可以引入栈或者队列，根据这种数据结构的特性，来达到循环过程中进行划分

void QuickSort2(int* nums, int numsSize)
{
	if (nums == nullptr || numsSize < 2) return;

	queue<int> q;
	q.push(0); 				// 1
	q.push(numsSize - 1); 	// 2

	while (!q.empty()) 		// 3
	{
		int left = q.front(); q.pop();
		int right = q.front(); q.pop();
		int pos = Partition(nums, left, right); // 4

		if (left < pos - 1) 					// 5
		{
			q.push(left);
			q.push(pos - 1);
		}
		if (pos + 1 < right)					// 6
		{
			q.push(pos + 1);
			q.push(right);
		}
	}
}

1. 定义队列后，初始值先将第一个元素下标（0）入队列。
2. 将最后一个元素下标（numsSize - 1)入队列。
3. 循环条件为判断队列是否为空，如果为空，说明所有数据划分完成。
4. 每次从队头取出两个下标，进入Partition函数划分。
5. 如果左边至少有两个元素，就将两个下标入队。
6. 如果右边至少有两个元素，就将两个下标入队。

运行实例:

2. 引入pair<>

void QuickSort3(int* nums, int numsSize)
{
	if (nums == nullptr || numsSize < 2) return;
	
	using Pair_int = pair<int, int>;
	queue<Pair_int> q;
	q.push(Pair_int(0, numsSize - 1));

	while (!q.empty())
	{
		Pair_int pos = q.front(); q.pop();
		int mid = Partition(nums, pos.first, pos.second);

		if (pos.first < mid - 1)
		{
			q.push(Pair_int(pos.first, mid - 1));
		}
		if (mid + 1 < pos.second)
		{
			q.push(Pair_int(mid + 1, pos.second));
		}
	}
}

三、改进方案

1. 随机划法

如果数据比较有序，那么快速排序会变得很慢，接近于O(n^2)，所以这第一个方法是让基准值变化，使序列不那么有序。

原始数据（比较有序），在普通划分后，遍历的过程接近于数组长度，时间复杂度接近于O(n^2)

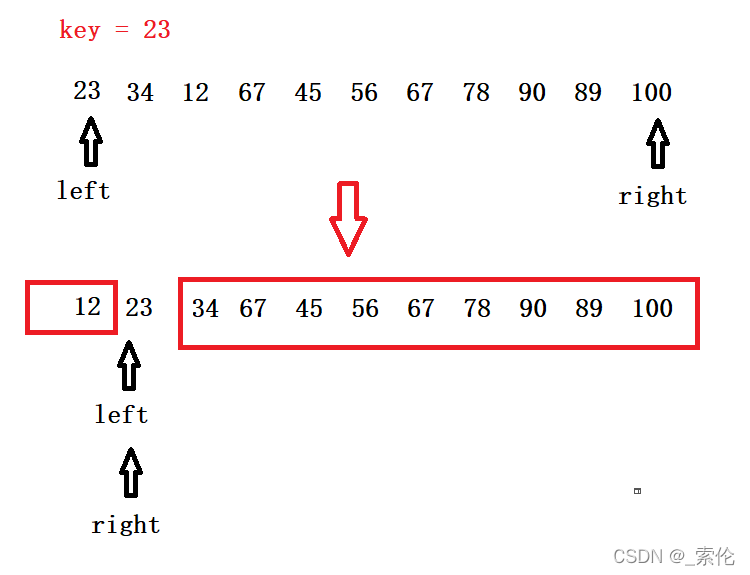
随机划分，交换基准值后：再进入Partition(),这样划分出来两边起码接近一半数据。

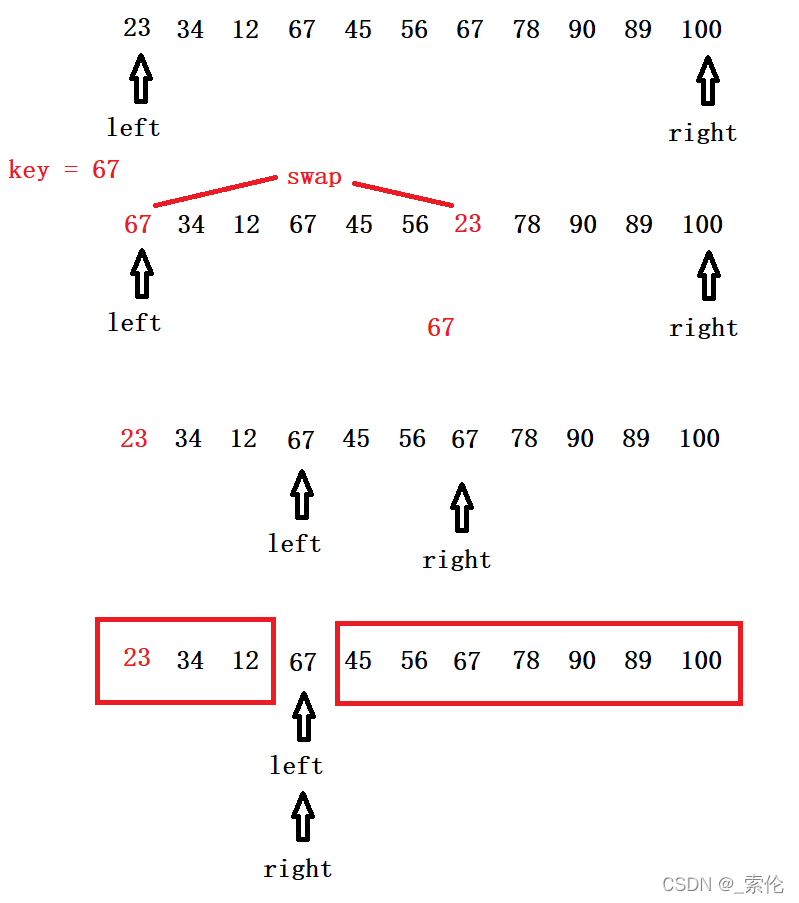
int RandPartition(int* nums, int left, int right)
{
	srand(time(nullptr));
	int pos = rand() % (right - left + 1) / 2 + left;
	std::swap(nums[left], nums[pos]);
	return Partition(nums, left, right);
}

2.三数取中法

利用左右两下标求出中间下标，与左边元素交换，使得基准值改变。

// 三位取中法
int MidPartition(int* nums, int left, int right)
{
	int mid = (right - left) / 2 + left;
	struct IndexNode
	{
		int key;
		int index;
		operator int() const {
			return key;
		}
	};
	struct IndexNode kL = { nums[left], left };
	struct IndexNode kM = { nums[mid], mid };
	struct IndexNode kR = { nums[right], right };

	std::priority_queue<IndexNode> hp;
	hp.push(kL); hp.push(kM); hp.push(kR);
	hp.pop();
	struct IndexNode pos = hp.top();

	std::swap(nums[kL.index], nums[pos.index]);

	return Partition(nums, left, right);
}

四、单项划分LeftPartition

像上面所提到的划分函数，实际上是左右双指针在移动，那如果只让单向走动，或者让对单链表进行快排（没有prev前驱指针），这该如何编写？

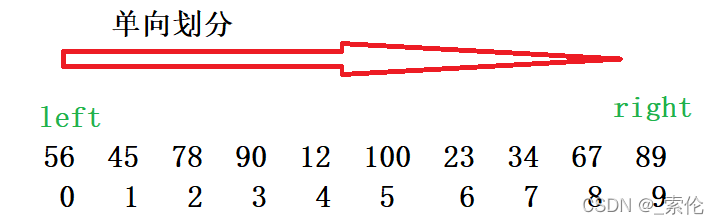
1.方法讲解

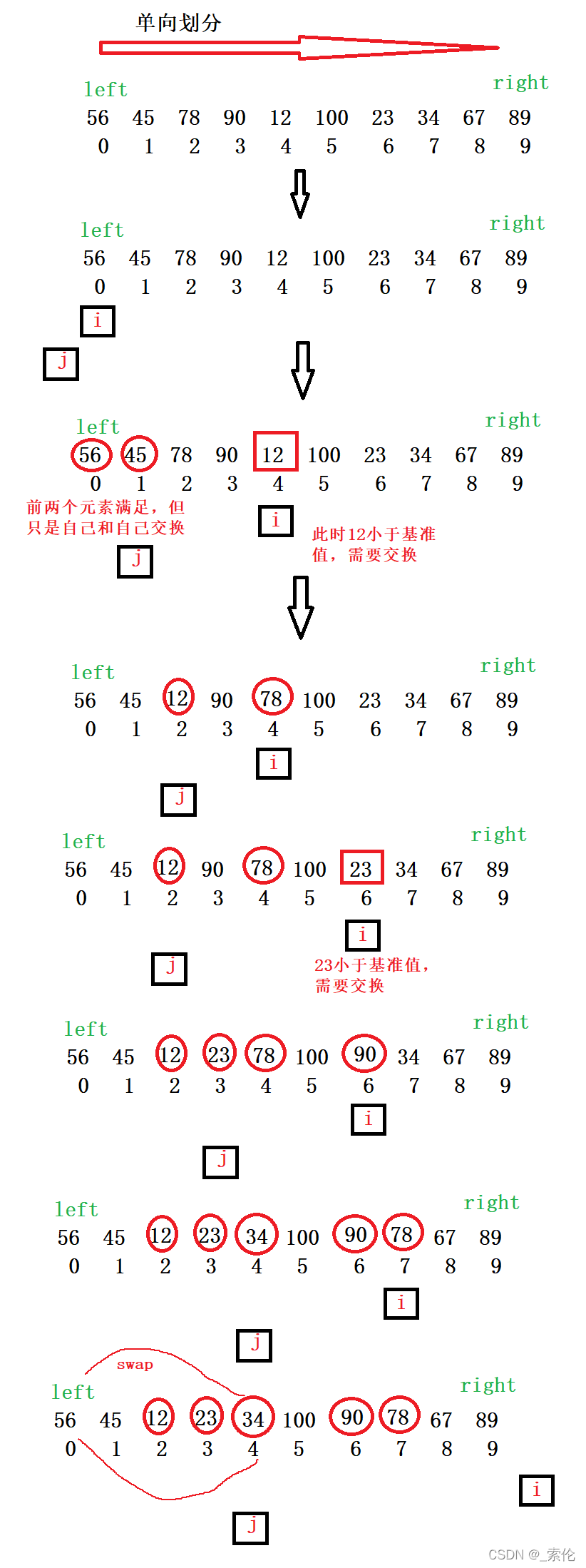
利用两个指针指向数组开头，定义完基准值后，一个指针先走，遇到小于基准值的元素，就将另一个指针往后移一位，并将两指针对应的元素交换。直到指针越界退出。最后将慢指针所指向的元素与首元素基准值交换，最终结果就是：基准值左边元素均小于它，右边元素均大于它。 返回值为最后的基准值所在下标。

1. 定义两个指针当作下标，初始为 0 和 -1，如图所示

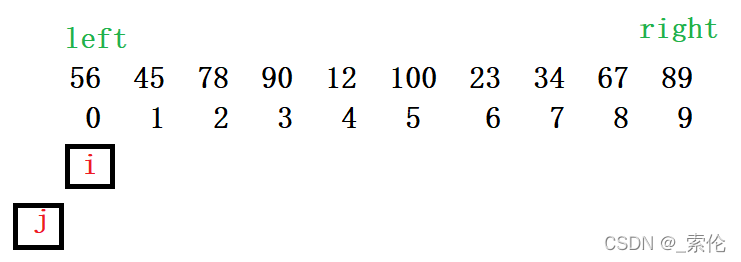
2. 仍然将第一个值当作基准值。让下标 i 往前走，如果遇到 比基准值小的，就先将 j下标往后走一步，再将 i 和 j对应的元素进行交换。这一步意味着小于基准值的都在数组前半部分，大于的都在右半部分。

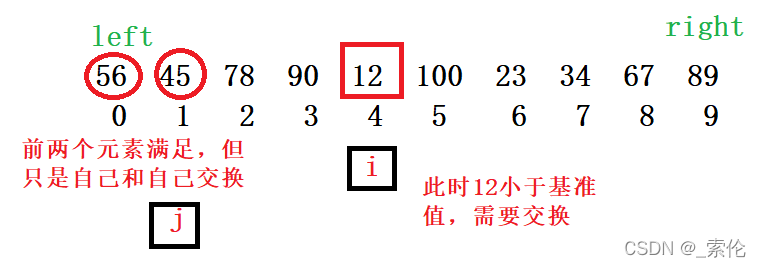
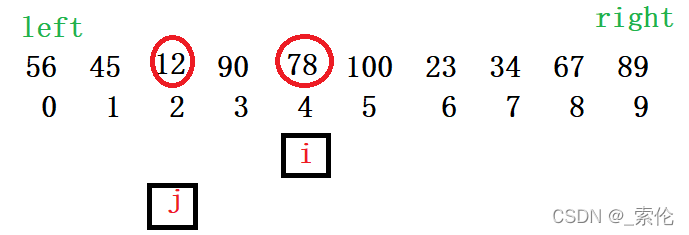
3. i下标继续往后走，遇到比基准值小的就和前面交换
   

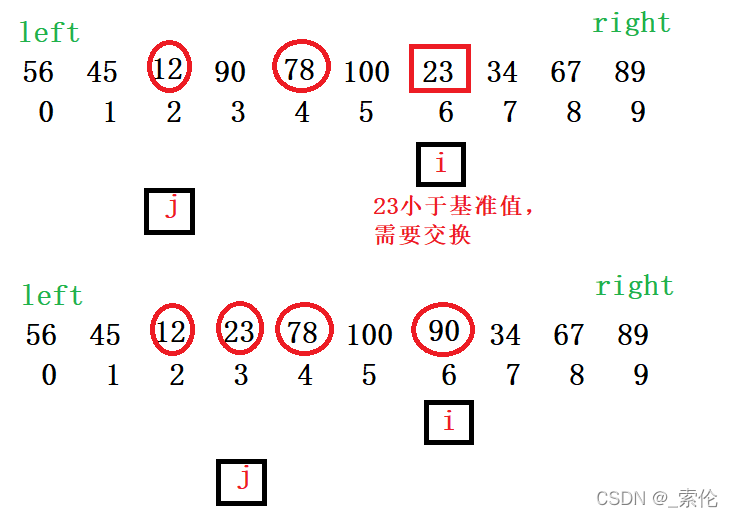
4. i 继续往后走，遇到小于基准值的就交换
   

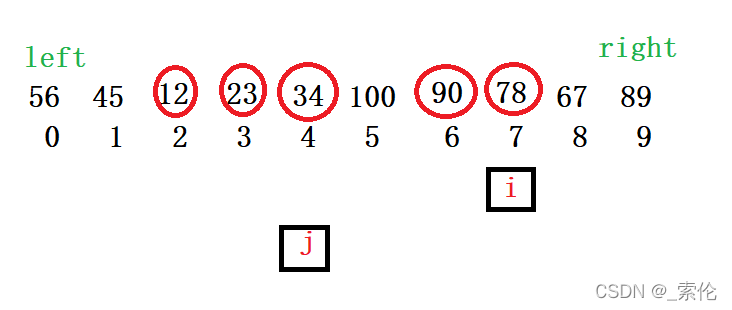
5. 最后 ，快指针越界后代表划分完成，再将首元素基准值和慢指针所指向的元素交换。

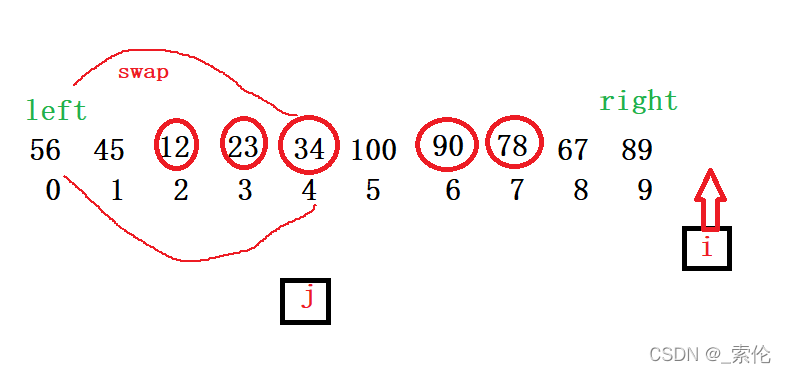
2.代码示例

// 单向划分
int LeftPartition(int* nums, int left, int right)
{
	int key = nums[left];
	int i = left, j = left - 1;

	while (i <= right)
	{
		if (nums[i] <= key)
		{
			++j;
			std::swap(nums[i], nums[j]);
		}
		++i;
	}
	std::swap(nums[j], nums[left]);

	return j;
}

五、同理所得的单链表快排

由于单链表是只有next域，没有prev前驱指针，所以刚好合适单项划分。

代码：

typedef int ElemType;
typedef struct ListNode
{
	ElemType data;
	ListNode* next;
}LinkList;

void ListQuickPartition(ListNode* head, ListNode* end)
{
	ListNode* i = head->next;
	ListNode* j = head;
	int key = i->data;

	while (i != end)
	{
		if (i->data <= key)
		{
			j = j->next;
			std::swap(i->data, j->data);
		}
		i = i->next;
	}
	std::swap(head->next->data, j->data);

	ListQuickPartition(head, j);
	ListQuickPartition(j, end);
}

END_快排代码

#include<iostream>
#include<queue>
using namespace std;

// quick Sort
// 划分函数
int Partition(int* nums, int left, int right)
{
	int key = nums[left];
	while (left < right)
	{
		while (left < right && nums[right] > key)
		{
			--right;
		}
		if (left < right) nums[left] = nums[right];

		while (left < right && nums[left] <= key)
		{
			++left;
		}
		if (left < right) nums[right] = nums[left];
	}
	nums[left] = key;

	return left;
}
// 随机画法
int RandPartition(int* nums, int left, int right)
{
	srand(time(nullptr));
	int pos = rand() % (right - left + 1) / 2 + left;
	std::swap(nums[left], nums[pos]);
	return Partition(nums, left, right);
}

// 三位取中法
int MidPartition(int* nums, int left, int right)
{
	int mid = (right - left) / 2 + left;
	struct IndexNode
	{
		int key;
		int index;
		operator int() const {
			return key;
		}
	};
	struct IndexNode kL = { nums[left], left };
	struct IndexNode kM = { nums[mid], mid };
	struct IndexNode kR = { nums[right], right };

	std::priority_queue<IndexNode> hp;
	hp.push(kL); hp.push(kM); hp.push(kR);
	hp.pop();
	struct IndexNode pos = hp.top();

	std::swap(nums[kL.index], nums[pos.index]);

	return LeftPartition(nums, left, right);
}
// 单向划分
int LeftPartition(int* nums, int left, int right)
{
	int key = nums[left];
	int i = left, j = left - 1;

	while (i <= right)
	{
		if (nums[i] <= key)
		{
			++j;
			std::swap(nums[i], nums[j]);
		}
		++i;
	}
	std::swap(nums[j], nums[left]);

	return j;
}

// 递归
void PassQuick(int* nums, int left, int right)
{
	if (left < right)
	{
		int pos = Partition(nums, left, right);

		PassQuick(nums, left, pos - 1);
		PassQuick(nums, pos + 1, right);
	}
}
void QuickSort(int* nums, int numsSize)
{
	if (nums == nullptr || numsSize <= 1) return;

	PassQuick(nums, 0, numsSize - 1);
}

// 队列 非递归
void QuickSort2(int* nums, int numsSize)
{
	if (nums == nullptr || numsSize < 2) return;

	queue<int> q;
	q.push(0);
	q.push(numsSize - 1);

	while (!q.empty())
	{
		int left = q.front(); q.pop();
		int right = q.front(); q.pop();
		int pos = Partition(nums, left, right);

		if (left < pos - 1)
		{
			q.push(left);
			q.push(pos - 1);
		}
		if (pos + 1 < right)
		{
			q.push(pos + 1);
			q.push(right);
		}
	}
}
// Pair非递归
void QuickSort3(int* nums, int numsSize)
{
	if (nums == nullptr || numsSize < 2) return;
	
	using Pair_int = pair<int, int>;
	queue<Pair_int> q;
	q.push(Pair_int(0, numsSize - 1));

	while (!q.empty())
	{
		Pair_int pos = q.front(); q.pop();
		int mid = MidPartition(nums, pos.first, pos.second);

		if (pos.first < mid - 1)
		{
			q.push(Pair_int(pos.first, mid - 1));
		}
		if (mid + 1 < pos.second)
		{
			q.push(Pair_int(mid + 1, pos.second));
		}
	}
}

// 输出函数
void PrintNums(const int* nums, int numsSize)
{
	if (nums == nullptr || numsSize < 0) return;
	for (int i = 0; i < numsSize; ++i)
	{
		cout << nums[i] << "  ";
	}
	cout << endl;
}

int main(void)
{
	int nums[] = { 52, 12, 78, 90, 34, 23, 100, 56, 45, 67, 89 };
	int numsSize = sizeof(nums) / sizeof(nums[0]);
	PrintNums(nums, numsSize);
	QuickSort3(nums, numsSize);
	PrintNums(nums, numsSize);

	return 0;
}

超强干货来袭

云风专访：近40年码龄，通宵达旦的技术人生