440. 字典序的第K小数字
【题目描述】
给定整数 n 和 k,返回 [1, n] 中字典序第 k 小的数字。
示例 1:
输入: n = 13, k = 2
输出: 10
解释: 字典序的排列是 [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9],所以第二小的数字是 10。
示例 2:
输入: n = 1, k = 1
输出: 1
提示:
1 <= k <= n <= 10^9
【解题思路】
字典序
简而言之,就是根据数字的前缀进行排序,
比如 10 < 9,因为 10 的前缀是 1,比 9 小。
再比如 112 < 12,因为 112 的前缀 11 小于 12。
- 题目要求找到字典序第 kk 小的数字,可以将所有的数字都转换成字符串,然后排序找到第 kk 小的数字即可,但显然时间复杂度不符合要求。我们利用字典树的特性将所有小于等于 nn 的数字按照字典序的方式进行重建,可以得到如下:
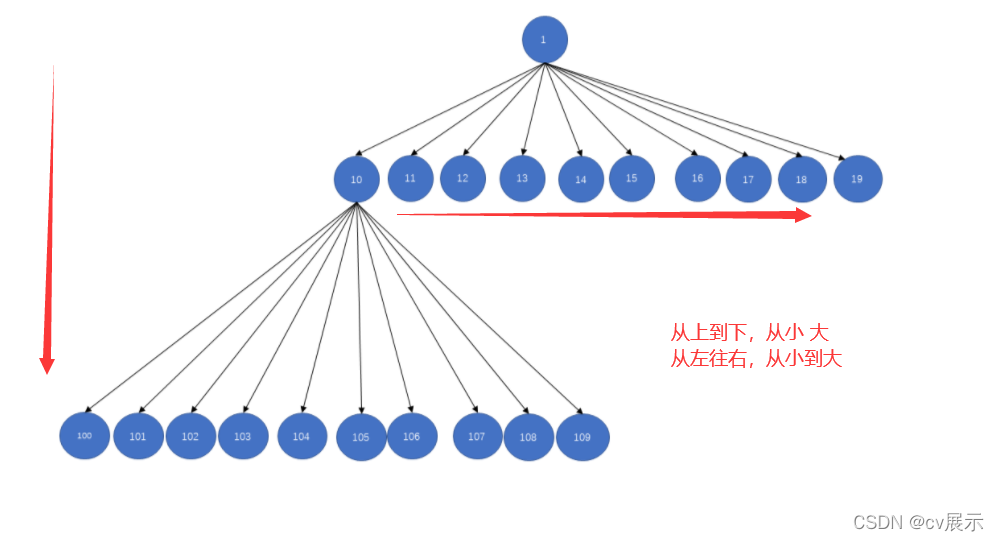
- 通过观察可以发现,前序遍历该字典树即可得到字典序从小到大的数字序列,遍历到第 kk 个节点即为第 kk 小的数字。
- 已知节点 i的子节点为(10×i,10×i+1,?,10×i+9),可以通过计算找到前序遍历第 k个节点即可
- 往下遍历记录第几小,当到达一个顶点是,我们可以记录他的子节点,子节点数量+第几小如果还小于k说明在后面,往右移动,如果大于的话说明这个第k小在子节点中
【AC代码】
import java.util.*;
public class Solution {
/**
* 字典树第k小
* @param n
* @param k
* @return
*/
public int findKthNumber(int n, int k) {
// 定义根节点
int root = 1;
k--;
while (k > 0){
// 获取子节点个数
int steps = getSteps(root , n);
// 小于k 说明不在子节点中,往右遍历
if(steps <= k){
k -= steps;
root++;
}else{
// 否则第k小在子结点中,遍历子节点
root *= 10;
k--;
}
}
return root;
}
// 计算子节点
public int getSteps(int root,int n){
int step = 0;
long left = root;
long right = root;
// 一层一层计算
while (left <= n){
step += Math.min(right, n) - left + 1;
left = left * 10;
right = right * 10 + 9;
}
return step;
}
}
129. 求根节点到叶节点数字之和
【题目描述】
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
- 例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:
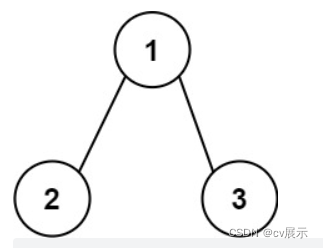
输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
示例 2:
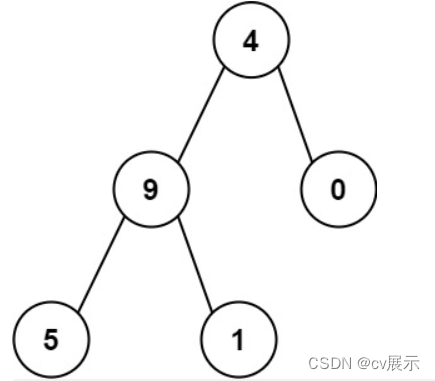
输入:root = [4,9,0,5,1]
输出:1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此,数字总和 = 495 + 491 + 40 = 1026
提示:
- 树中节点的数目在范围 [1, 1000] 内
- 0 <= Node.val <= 9
- 树的深度不超过 10
【解题思路】dfs遍历到叶子节点返回计算结果
【AC代码】
class Solution {
public int sumNumbers(TreeNode root) {
return dfs(root,0);
}
public int dfs(TreeNode root,int sum){
if(root == null){
return 0;
}
int s = sum * 10 + root.val;
// 叶子节点返回
if(root.left == null && root.right == null){
return s;
}
// 递归计算结果
return dfs(root.right,s) + dfs(root.left,s);
}
}
每日打卡: 380. O(1) 时间插入、删除和获取随机元素
class RandomizedSet {
List<Integer> list;
Map<Integer,Integer> map;
Random random;
public RandomizedSet() {
list = new ArrayList<>();
map = new HashMap<>();
random = new Random();
}
public boolean insert(int val) {
if(map.containsKey(val)){
return false;
}
int index = list.size();
list.add(val);
map.put(val,index);
return true;
}
public boolean remove(int val) {
if(!map.containsKey(val)){
return false;
}
int index = map.get(val);
int last = list.get(list.size() - 1);
list.set(index,last);
map.put(last,index);
list.remove(list.size() - 1);
map.remove((Object)val);
return true;
}
public int getRandom() {
int index = random.nextInt(list.size());
return list.get(index);
}
}
