[数据结构与算法]牛客：缆车（LCA）

牛客小白月赛

题意：

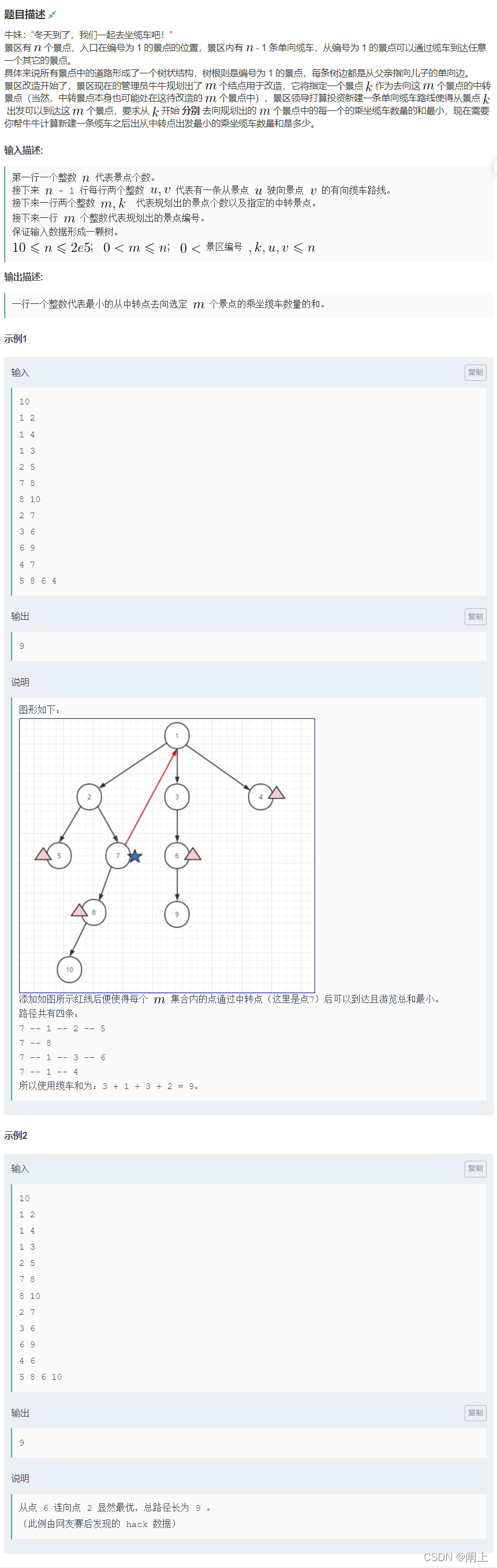
• 给定一颗特别的 有向 树，从 1号根节点 往下能走到所有点，看图即可。
• 树上画出 m 个景点 和 一个 中转点 K，给这棵树加一条边，使得 K 去往 m 个景点的距离和最小，求这个最小距离。

思路：

• 一开始想简单了，直接当成无向树给 LCA 加边，显然大wa特wa。
• 事实上应该分情况讨论：

首先这条边的一端肯定是 K 点。

1. 这 m + 1 个点的最近公共祖先（LCA）为 K。

• 显然这种情况，K 已经能往下走到所有点了，所以只需要加一条能减距离最大的边。
• 这个贡献的计算为 $Max(0，某点子树内景点个数?(到K的距离?1))$
• 减一是因为加的边也要算距离，有可能不加反而最好（只有一个景点同时和 K 重合的时候）
• 只需枚举所有点即可。

2. 这 m + 1 个点的 LCA 不是 K。

• 这种情况下，K 往下走是走不到所有景点的。加的边不仅要考虑 贡献 大，还要保证能走到所有点。

• 首先这条边不会加到 K 以下，因为这样会有点走不到。所以 K 以下的点可以先计算到 K 的距离，而其他点，我们累计它们到根节点的距离。（可以理解成先加边到根节点）

• 这条边连的点，必须保证往下的点数 >= $总景点数?K下面的点数$，而贡献应该等于 $Max(0，该点子树内景点个数（要除去K子树内的）?(根节点到该点的距离?1))$

• 判断某点是否在 K 子树内可以用 LCA

细节看注释吧，这题是真难讲

$Code:$

#include<bits/stdc++.h>
#include<unordered_map>
#define mem(a,b) memset(a,b,sizeof a)
#define cinios (ios::sync_with_stdio(false),cin.tie(0),cout.tie(0))
#define sca scanf
#define pri printf
#define forr(a,b,c) for(int a=b;a<=c;a++)
#define rfor(a,b,c) for(int a=b;a>=c;a--)
#define all(a) a.begin(),a.end()
#define oper(a) (operator<(const a& ee)const)
#define endl "\n"
using namespace std;

typedef long long ll;
typedef pair<int, int> PII;

double DNF = 1e17;
const int N = 200010, M = 400010, MM = 110;
int INF = 0x3f3f3f3f, mod = 1e9 + 7;
ll LNF = 0x3f3f3f3f3f3f3f3f;
int n, m, k, T, S, D, K;
int h[N], e[M], ne[M], idx;
int dep[N], cnt[N], dist[N];
int f[N][19], a[N];
bool st[N];

void add(int a, int b) {
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void bfs(int x) {
	mem(dep, -1);
	queue<int> q;
	q.push(x);
	dep[0] = 0, dep[x] = 1;
	while (q.size())
	{
		int t = q.front();
		q.pop();
		for (int i = h[t]; ~i; i = ne[i]) {
			int j = e[i];
			if (dep[j] == -1) {
				q.push(j);
				dep[j] = dep[t] + 1;
				dist[j] = dist[t] + 1;
				f[j][0] = t;
				for (int k = 1; k <= 18; k++)//bug —— 加分号...找了一亿年
					f[j][k] = f[f[j][k - 1]][k - 1];
			}
		}
	}
}

int lca(int a, int b) {
	if (dep[a] < dep[b])swap(a, b);
	for (int i = 18; i >= 0; i--)
		if (dep[f[a][i]] >= dep[b])
			a = f[a][i];
	if (a == b)return a;
	for (int i = 18; i >= 0; i--)
		if (f[a][i] != f[b][i]) {
			a = f[a][i];
			b = f[b][i];
		}
	return f[a][0];
}

void dfs_yu(int x, int fa) {
	if (st[x])cnt[x]++;
	for (int i = h[x]; ~i; i = ne[i]) {
		int j = e[i];
		if (j == fa)continue;
		dfs_yu(j, x);
		cnt[x] += cnt[j];//预处理维护某子树内景点个数
	}
}

void solve() {
	cin >> n;
	mem(h, -1);

	forr(i, 2, n) {
		int a, b;
		cin >> a >> b;
		add(a, b);
	}
	bfs(1);

	cin >> m >> k;
	int p = k;
	forr(i, 1, m) {
		cin >> a[i];
		p = lca(p, a[i]);
		st[a[i]] = true;
	}
	dfs_yu(1, -1);

	if (p == k) {
		ll ans = 0;
		forr(i, 1, m)ans += dist[a[i]] - dist[k];//不加边的距离
		ll mx = -LNF;
		forr(i, 1, n)//找一个最大贡献
			mx = max(mx, 1ll * (dist[i] - dist[k] - 1) * cnt[i]);

		cout << min(ans, ans - mx);
	}
	else {
		ll ans = 0;
		forr(i, 1, m) {
			if (lca(a[i], k) == k)ans += dist[a[i]] - dist[k];//K子树内
			else ans += dist[a[i]];//否则累计到根节点的距离（先假设连边到根节点）
		}

		ll mx = -LNF;
		forr(i, 1, n) {
			int pp = lca(i, k), res = 0;

			if (pp == k)continue;
			else if (pp == i)res = cnt[i];
			else res = cnt[i] + cnt[k];

			if (res != m)continue;//判断该点能不能走到所有景点
			//但计算时不能把 K子树 内的景点计算进来
			res -= cnt[k];

			mx = max(mx, 1ll * (dist[i] - 1) * res);
		}
		/*cout << mx << endl;*/

		cout << ans - mx;//无论如何都是要加边的，即使贡献为负
	}
}

int main() {
	cinios;
	T = 1;
	while (T--)solve();
	return 0;
}
/*
*/

超强干货来袭

云风专访：近40年码龄，通宵达旦的技术人生