[数据结构与算法]二叉查找树的递归实现（基于java语言）

二叉查找树的递归实现

一、基本概念

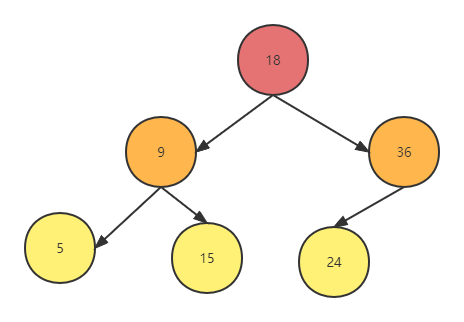
二叉查找树是一种特殊的二叉树，特殊就特殊在它的节点的值上，在二叉查找树中任意一个节点的左孩子的关键字，一定小于根节点，右孩子的关键字一定大于根节点

二、二叉查找树的基本操作

2.1 插入

1. 如果根节点为空，那么新插入的节点就是根节点
2. 如果根节点不为空，那么让cur指向根节点root，其中cur表示当前正在访问的节点。不妨设新插入的关键字是key，比较cur.key和key的大小，如果key更大，那么让cur=cur.right（因为当前新插入的关键字更大，所以key只能插入在以cur为根节点的树的右孩子上），反之则让cur=cur.left。直到cur为NULL，那么将key插入到cur的父亲节点的左孩子或者右孩子上，到底是左还是右取决于key和cur.parent.key的大小。
3. 这里给出递归的代码实现

   /**
    * 向二叉查找树中插入一个新的键值对
    *
    * @param key   关键字
    * @param value 值
    */
   public void insert(T key, V value) {
       root = insertHelper(key, value, root);
   }
   
   /**
    * 将新的键值对插入到以root为根节点的二查找树中
    *
    * @param key   关键字
    * @param value 值
    * @param root  根节点
    * @return 返回插入后的新的树的根节点
    */
   private TreeNode<T, V> insertHelper(T key,
                                       V value,
                                       TreeNode<T, V> root) {
       if (root == null) {
           root = new TreeNode<>(key, value, null, null);
       } else if (root.key.compareTo(key) < 0) {
           // 如果当前节点关键字比要插入的关键字小
           root.right = insertHelper(key, value, root.right);
       } else if (root.key.compareTo(key) > 0) {
           root.left = insertHelper(key, value, root.left);
       }
       // 如果相等的情况下，什么也不做
       return root;
   }
   

2.2 删除

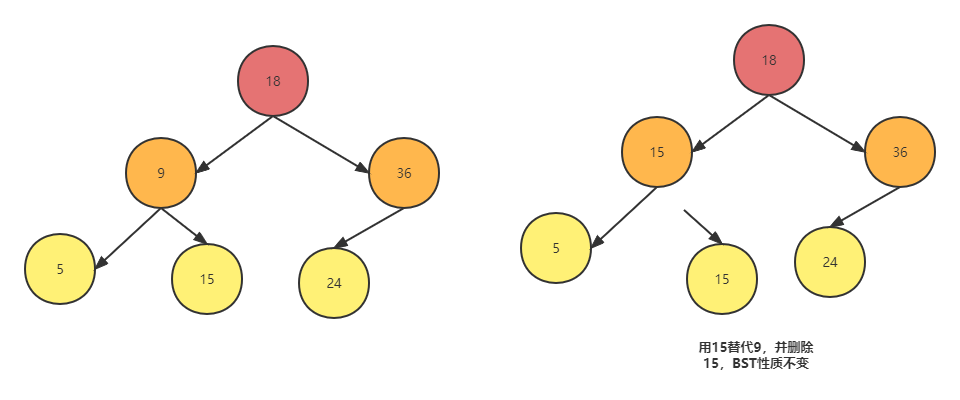
二叉查找树的删除算法比插入算法复杂许多，但是搞清楚了逻辑，也就没什么复杂的了，掌握删除算法要掌握一个核心的思想，就是将对一个节点的删除转换为对另外一个节点的删除，为什么可以这样呢？主要是由bst的中序遍历的顺序决定的，对上图中的bst而言，我们可以发现其中序遍历的顺序是：5 9 15 18 24 36，假设我们要删除9，我们从图中可以看到，如果删除9将会导致需要调整许多的指针，显得很麻烦，但是我们通过中序序列可以看出，我们可以把15放到9的位置上，然后删去15即可，15是一个叶子节点，删除要简单许多，同时还能保证bst的性质不变。有了这个思想我们看一下具体的删除步骤

1. 遍历BST，找到我们要删除的节点，如果某个节点关键字和我们要删除的关键字相等，那么这个节点就是我们要删除的节点
2. 判断被删除的节点属于下面三种情况的哪一种
   （1）被删除的节点是叶子节点，如果满足这种情况，那么直接让该节点的父亲节点对应的指针，指向null即可，当然如果当前节点为根节点（根节点没有父亲节点），那么直接让root指针指向null即可（整棵树变为空）
   （2）被删除的节点只有一个孩子节点，如果满足这种情况，那么直接让该节点的父亲节点对应的指针指向被删除的节点的非空孩子节点即可，同样被删除的节点也可能是根节点，如果是根节点，那么直接让根节点变为它的非空孩子节点即可
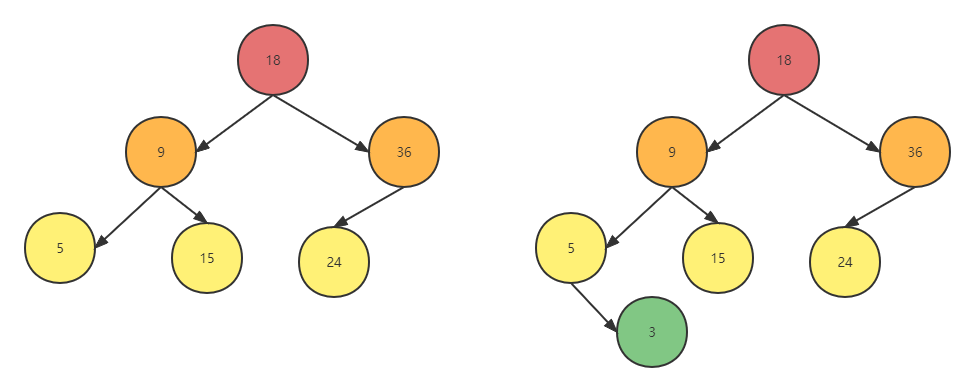
   （3）被删除的节点有两个孩子节点，这种情况最为复杂，但是删除算法的巧妙就在于，我们可以将这种最复杂的情况转换为（1）和（2），具体的做法就是，如果被删除的节点有两个孩子，那么找到该节点的右孩子的最小关键字节点，然后使用该最小关键字节点的关键字替换被删除的节点的关键字，之后删除该最小关键字节点即可。

   我们可以证明这个最小关键字节点要么是叶子节点，要么只有一个孩子，因为最小关键字节点是BST中最小值，而一棵BST的最小值一定是BST的最左边的节点，最多有如下两种情况：左边的最小关键字是5，是叶子节点，而右边的最小关键字也是5，没有左孩子，只有右孩子，刚好就是（1）和（2）中的情况
   

3. 递归的删除代码

   /**
    * 删除二叉查找树中指定的关键字
    *
    * @param key 关键字
    * @return 如果删除成功，返回删除的值，否则返回null
    */
   public V delete(T key) {
       Pair<TreeNode<T, V>, V> delInfo = deleteHelper(key, root);
       root = delInfo.getKey();
       return delInfo.getValue();
   }
   
   /**
    * 递归的删除以root为根的二查找树，并且返回删除后的新的二叉查找树的
    * 根节点
    *
    * @param key  关键字
    * @param root 根节点引用
    * @return 返回删除后的新的bst的根节点引用
    */
   private Pair<TreeNode<T, V>, V> deleteHelper(T key, TreeNode<T, V> root) {
       if (root == null) {
           // 如果根节点为null，新的根也为null，值为null
           return new Pair<>(null, null);
       }
   
       if (root.key.compareTo(key) < 0) {
           // 待删除的关键字在右孩子，这里不能直接返回pair，因为这个pair存放的信息
           // 是root的右孩子的，这里返回，必须返回的是root的信息，因此下面需要重新
           // 构建root的信息
           Pair<TreeNode<T, V>, V> pair = deleteHelper(key, root.right);
           root.right = pair.getKey();
           return new Pair<>(root, pair.getValue());
       } else if (root.key.compareTo(key) > 0) {
           // 待删除的关键字在左孩子
           Pair<TreeNode<T, V>, V> pair = deleteHelper(key, root.left);
           root.left = pair.getKey();
           return new Pair<>(root, pair.getValue());
       } else {
           if (root.left == null && root.right == null) {
               // 如果root是叶子节点
               return new Pair<>(null, root.value);
           }
           // root左右孩子至少有一个不为null
           if (root.left == null) {
               // root的左孩子为null，那么右孩子一定不为null
               return new Pair<>(root.right, root.value);
           } else if (root.right == null) {
               return new Pair<>(root.left, root.value);
           } else {
               // 如果两个都不为null
               Pair<TreeNode<T, V>, V> delInfo = findAndDeleteMin(root.right);
               root.right = delInfo.getKey();
               Pair<TreeNode<T, V>, V> pair = new Pair<>(root, root.value);
               root.value = delInfo.getValue();
               return pair;
           }
       }
   }
   
   /**
    * 删除bst中具有最小关键字的那个节点
    *
    * @param root 根节点
    * @return 返回一个Pair对象，其中Pair的第一个值是删除最小关键字后，新的
    * bst的根节点，第二个值是被删除的最小关键字对应的值
    */
   private Pair<TreeNode<T, V>, V> findAndDeleteMin(TreeNode<T, V> root) {
       if (root == null) {
           return new Pair<>(null, null);
       }
   
       TreeNode<T, V> mostLeft = root.left;
       if (mostLeft == null) {
           return new Pair<>(root.right, root.value);
       }
   
       TreeNode<T, V> pre = root;
       while (mostLeft.left != null) {
           pre = mostLeft;
           mostLeft = mostLeft.left;
       }
       if (mostLeft.right != null) {
           pre.left = mostLeft.right;
       } else {
           pre.left = null;
       }
   
       return new Pair<>(root, mostLeft.value);
   }
   

2.3 查找

二叉查找树的查找算法十分的简单，这里给出的是也是一个递归的写法，并且很容易转成非递归的写法，通过不断的比较关键字即可完成对应关键字的查找

/**
     * 根据指定的关键字查找该关键字对应的值
     *
     * @param key 关键字
     * @return 返回key对应的值，如果不存在，返回null
     */
    public V find(T key) {
        TreeNode<T, V> node = findHelper(key, root);
        return node == null ? null : node.value;
    }

    /**
     * 在以root为根的二叉查找树中查找指定的关键字对应的值
     *
     * @param key  关键字
     * @param root 根节点引用
     * @return 如果查找成功，返回节点引用，否则返回null
     */
    private TreeNode<T, V> findHelper(T key, TreeNode<T, V> root) {
        if (root == null) {
            return null;
        }
        if (root.key.compareTo(key) < 0) {
            return findHelper(key, root.right);
        } else if (root.key.compareTo(key) > 0) {
            return findHelper(key, root.left);
        } else {
            return root;
        }
    }

三、时间复杂度

BST的增删改查的时间复杂度均是O(logn)级别

四、完整代码

import javafx.util.Pair;

/**
 * 使用递归的方式实现二叉查找树
 *
 * @author 西城风雨楼
 */
public class BinarySearchTree<T extends Comparable<T>, V> {
    public TreeNode<T, V> root;

    /**
     * 创建一棵空的二叉搜索树
     *
     * @param <T> key类型
     * @param <V> 值类型
     * @return 返回空的二叉查找树
     */
    public static <T extends Comparable<T>, V> BinarySearchTree<T, V> getInstance() {
        return new BinarySearchTree<>();
    }

    /**
     * 向二叉查找树中插入一个新的键值对
     *
     * @param key   关键字
     * @param value 值
     */
    public void insert(T key, V value) {
        root = insertHelper(key, value, root);
    }

    /**
     * 将新的键值对插入到以root为根节点的二查找树中
     *
     * @param key   关键字
     * @param value 值
     * @param root  根节点
     * @return 返回插入后的新的树的根节点
     */
    private TreeNode<T, V> insertHelper(T key,
                                        V value,
                                        TreeNode<T, V> root) {
        if (root == null) {
            root = new TreeNode<>(key, value, null, null);
        } else if (root.key.compareTo(key) < 0) {
            // 如果当前节点关键字比要插入的关键字小
            root.right = insertHelper(key, value, root.right);
        } else if (root.key.compareTo(key) > 0) {
            root.left = insertHelper(key, value, root.left);
        }
        // 如果相等的情况下，什么也不做
        return root;
    }

    /**
     * 根据指定的关键字查找该关键字对应的值
     *
     * @param key 关键字
     * @return 返回key对应的值，如果不存在，返回null
     */
    public V find(T key) {
        TreeNode<T, V> node = findHelper(key, root);
        return node == null ? null : node.value;
    }

    /**
     * 在以root为根的二叉查找树中查找指定的关键字对应的值
     *
     * @param key  关键字
     * @param root 根节点引用
     * @return 如果查找成功，返回节点引用，否则返回null
     */
    private TreeNode<T, V> findHelper(T key, TreeNode<T, V> root) {
        if (root == null) {
            return null;
        }
        if (root.key.compareTo(key) < 0) {
            return findHelper(key, root.right);
        } else if (root.key.compareTo(key) > 0) {
            return findHelper(key, root.left);
        } else {
            return root;
        }
    }

    /**
     * 查找二叉查找树中的最大值
     *
     * @return 返回bst中的最大值
     */
    public V findMax() {
        TreeNode<T, V> cur = root;
        while (cur != null && cur.right != null) {
            cur = cur.right;
        }
        return cur == null ? null : cur.value;
    }

    /**
     * 查找二叉查找树中的最小值
     *
     * @return 返回bst中的最小值
     */
    public V findMin() {
        TreeNode<T, V> cur = root;
        while (cur != null && cur.left != null) {
            cur = cur.left;
        }
        return cur == null ? null : cur.value;
    }

    /**
     * 删除二叉查找树中指定的关键字
     *
     * @param key 关键字
     * @return 如果删除成功，返回删除的值，否则返回null
     */
    public V delete(T key) {
        Pair<TreeNode<T, V>, V> delInfo = deleteHelper(key, root);
        root = delInfo.getKey();
        return delInfo.getValue();
    }

    /**
     * 递归的删除以root为根的二查找树，并且返回删除后的新的二叉查找树的
     * 根节点
     *
     * @param key  关键字
     * @param root 根节点引用
     * @return 返回删除后的新的bst的根节点引用
     */
    private Pair<TreeNode<T, V>, V> deleteHelper(T key, TreeNode<T, V> root) {
        if (root == null) {
            // 如果根节点为null，新的根也为null，值为null
            return new Pair<>(null, null);
        }

        if (root.key.compareTo(key) < 0) {
            // 待删除的关键字在右孩子，这里不能直接返回pair，因为这个pair存放的信息
            // 是root的右孩子的，这里返回，必须返回的是root的信息，因此下面需要重新
            // 构建root的信息
            Pair<TreeNode<T, V>, V> pair = deleteHelper(key, root.right);
            root.right = pair.getKey();
            return new Pair<>(root, pair.getValue());
        } else if (root.key.compareTo(key) > 0) {
            // 待删除的关键字在左孩子
            Pair<TreeNode<T, V>, V> pair = deleteHelper(key, root.left);
            root.left = pair.getKey();
            return new Pair<>(root, pair.getValue());
        } else {
            if (root.left == null && root.right == null) {
                // 如果root是叶子节点
                return new Pair<>(null, root.value);
            }
            // root左右孩子至少有一个不为null
            if (root.left == null) {
                // root的左孩子为null，那么右孩子一定不为null
                return new Pair<>(root.right, root.value);
            } else if (root.right == null) {
                return new Pair<>(root.left, root.value);
            } else {
                // 如果两个都不为null
                Pair<TreeNode<T, V>, V> delInfo = findAndDeleteMin(root.right);
                root.right = delInfo.getKey();
                Pair<TreeNode<T, V>, V> pair = new Pair<>(root, root.value);
                root.value = delInfo.getValue();
                return pair;
            }
        }
    }

    /**
     * 删除bst中具有最小关键字的那个节点
     *
     * @param root 根节点
     * @return 返回一个Pair对象，其中Pair的第一个值是删除最小关键字后，新的
     * bst的根节点，第二个值是被删除的最小关键字对应的值
     */
    private Pair<TreeNode<T, V>, V> findAndDeleteMin(TreeNode<T, V> root) {
        if (root == null) {
            return new Pair<>(null, null);
        }

        TreeNode<T, V> mostLeft = root.left;
        if (mostLeft == null) {
            return new Pair<>(root.right, root.value);
        }

        TreeNode<T, V> pre = root;
        while (mostLeft.left != null) {
            pre = mostLeft;
            mostLeft = mostLeft.left;
        }
        if (mostLeft.right != null) {
            pre.left = mostLeft.right;
        } else {
            pre.left = null;
        }

        return new Pair<>(root, mostLeft.value);
    }

    /**
     * 返回二叉查找树的中序遍历结果，如果创建的二叉查找树是正确的
     * 那么该中序遍历的结果应该是升序的
     *
     * @return 返回二查找树的中序遍历结果
     */
    public String inOrder() {
        StringBuilder in = new StringBuilder();
        if (root == null) {
            return in.toString();
        }

        TreeNode<T, V> cur = root;

        while (cur != null) {
            if (cur.left != null) {
                TreeNode<T, V> mostRight = cur.left;
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                if (mostRight.right == null) {
                    // 如果是第一次访问，那么对于中序遍历来说，不应该记录
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                } else {
                    mostRight.right = null;
                    // 如果是第二次访问，那么应该进行访问
                    in.append(cur.value);
                }
            } else {
                // 如果没有左孩子，那么需要直接访问
                in.append(cur.value);
            }
            cur = cur.right;
        }

        return in.toString();
    }

    /**
     * 二叉搜索树的节点类型
     *
     * @param <T> key类型
     * @param <V> 值类型
     */
    private static class TreeNode<T extends Comparable<T>, V> {
        public T key;
        public V value;
        public TreeNode<T, V> left;
        public TreeNode<T, V> right;

        public TreeNode(T key,
                        V value,
                        TreeNode<T, V> left,
                        TreeNode<T, V> right) {
            this.key = key;
            this.value = value;
        }
    }

    public static void main(String[] args) {
        BinarySearchTree<Integer, Integer> bst = new BinarySearchTree<>();
        bst.insert(1, 1);
        bst.insert(2, 2);
        bst.insert(3, 3);
        bst.insert(4, 4);
        bst.insert(10, 10);
        bst.insert(6, 6);
        System.out.println("delete:");
        System.out.println(bst.delete(1));
        System.out.println(bst.inOrder());
    }
}

超强干货来袭

云风专访：近40年码龄，通宵达旦的技术人生