LeetCode算法入门(第五十七天)
递归/回溯
47.全排列Ⅱ
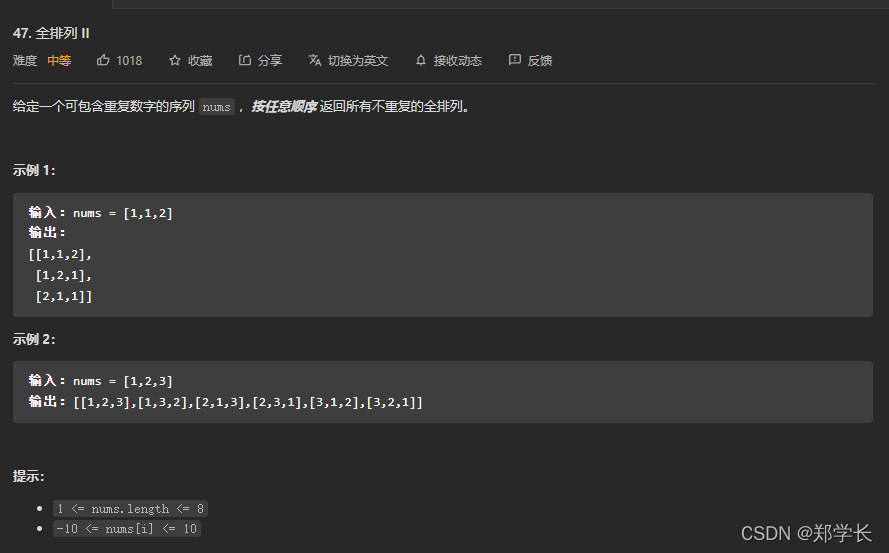
①排列是有序的,也就是说 [1,2] 和 [2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方。元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题时for循环那里i=0而不是i=startIndex。 也可以使用不带startIndex参数的递归函数,如题解中的注释部分。
②有重复的元素,所以需要去重。
③同一个元素不能重复选取,所以递归时,若传入参数startIndex则传入i+1
class Solution {
public:
vector<int> path;
vector<vector<int>> result;
//void bracktracking(vector<int>& nums, vector<bool> used)
void bracktracking(vector<int>& nums, vector<bool> used, int startIndex){
//当路径大小等于给定的数组大小说明找到了一组
if(path.size() == nums.size()){
result.push_back(path);
return;
}
//可以选择之前选过的,所以不用startIndex来缩小范围
for(int i = 0; i < nums.size(); i++){
if(i > 0 && nums[i] == nums[i-1] && used[i-1] == false){
continue;
}
//if(used[i] == true){
//continue;
//}
if(used[i] == false){
path.push_back(nums[i]);
used[i] = true;
bracktracking(nums, used, i+1); //元素不能重复选取
//bracktracking(nums, used);
used[i] = false;
path.pop_back();
}
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
vector<bool> used(nums.size(), false);
path.clear();
result.clear();
sort(nums.begin(), nums.end());
bracktracking(nums, used, 0);
//bracktracking(nums, used);
return result;
}
};
39.组合总和
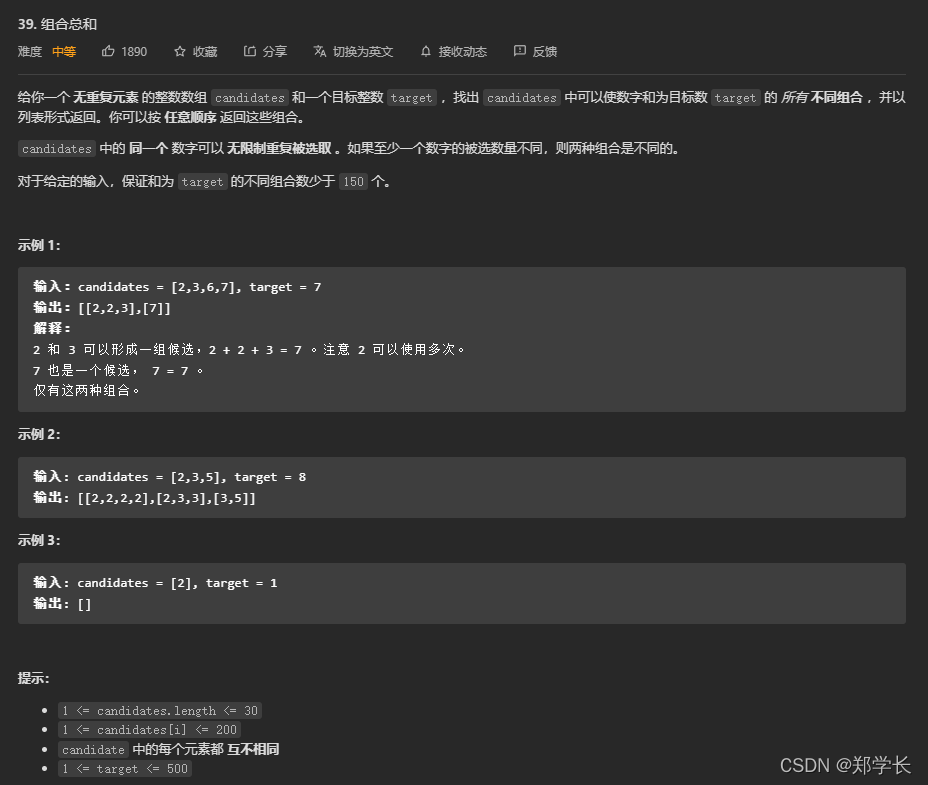
①组合与排列不同,组合与子集一样都是无序的,即在for循环时取过的元素不能再取,所以在for循环那里使用i=startIndex,而不是i=0,每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围,就是要靠startIndex;
②给定的数组中无重复元素,所以无需去重;
③由于同一数字可以重复被选取,所以递归时传入的参数是i,而不是i+1。
class Solution {
public:
vector<int> path;
vector<vector<int>> result;
void bracktracking(vector<int>& candidates, int target, int sum, int startIndex){
if(sum > target){
return;
}
if(sum == target)
{
result.push_back(path);
return;
}
if(sum < target)
{
for(int i = startIndex; i < candidates.size(); i++){
path.push_back(candidates[i]);
sum += candidates[i];
bracktracking(candidates, target, sum, i); //因为同一数字可以重复选取,所以i不需要+1
sum -= candidates[i];
path.pop_back();
}
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
path.clear();
result.clear();
bracktracking(candidates, target, 0, 0);
return result;
}
};
40.组合总和Ⅱ
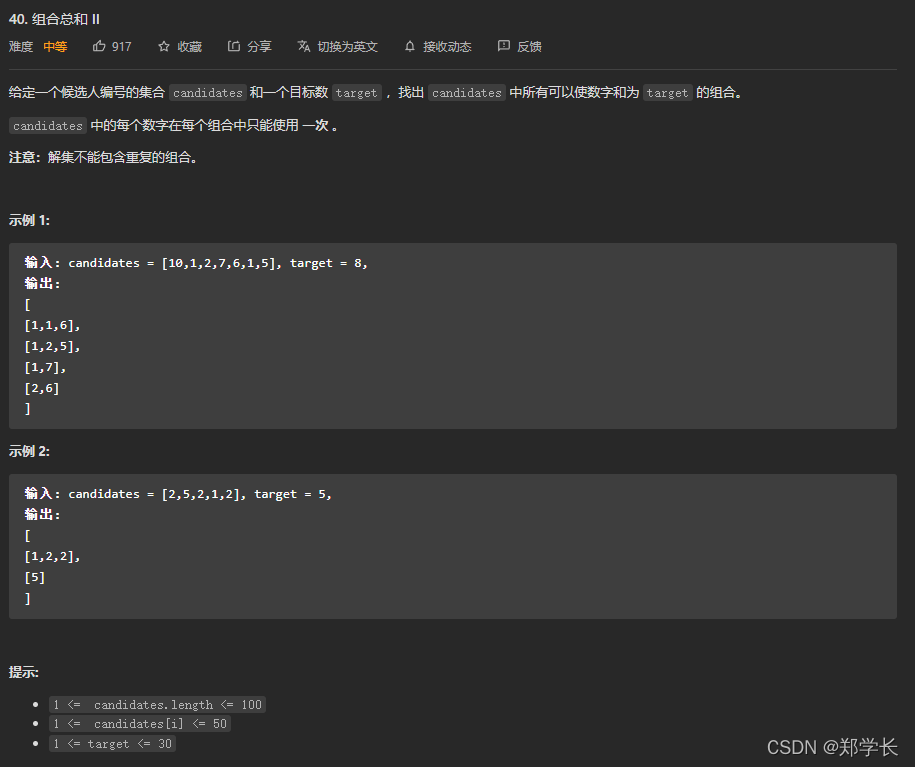
本题与上一题的区别在于:
①题中表明每个数字在每个组合中只能使用一次, 这里的只能使用一次结合示例1来理解,输出里[1,1,6],这里的1是重复的元素但不是同一个元素,输入里有两个数值为1的元素,每一个使用了一次。 所以在递归时需要传入的是i+1。
②以及数组中有重复元素,所以需要去重
class Solution {
public:
vector<int> path;
vector<vector<int>> result;
void bracktracking(vector<int>& candidates, int startIndex, int sum, int target, vector<bool> used){
if(sum > target){
return;
}
if(sum == target){
result.push_back(path);
return;
}
//unordered_set<int> uset;
if(sum < target){
for(int i = startIndex; i < candidates.size(); i++){
// if(uset.find(candidates[i]) != uset.end()){
// continue;
// }
// uset.insert(candidates[i]);
//candidates[i] == candidates[i-1]说明有重复的元素,而used[i-1]=false表示在同一层重复选取了,
if(i > 0 && candidates[i] == candidates[i-1] && used[i-1] == false){
continue;
}
sum += candidates[i];
path.push_back(candidates[i]);
used[i] = true;
bracktracking(candidates, i + 1, sum, target, used);
//回溯
used[i] = false;
sum -= candidates[i];
path.pop_back();
}
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
vector<bool> used(candidates.size(), false); //记录是否选取过
path.clear();
result.clear();
sort(candidates.begin(), candidates.end()); //去重要排序
bracktracking(candidates, 0, 0, target, used);
return result;
}
};
