旋转数组
1.查找最小值
题目描述:
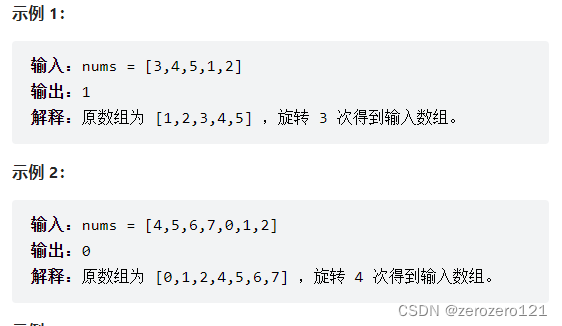
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,2] - 若旋转
7次,则可以得到[0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
(1)数组中的值各不相同
算法分析:
因为需要在O(log n)时间内完成算法,所以首先考虑二分。
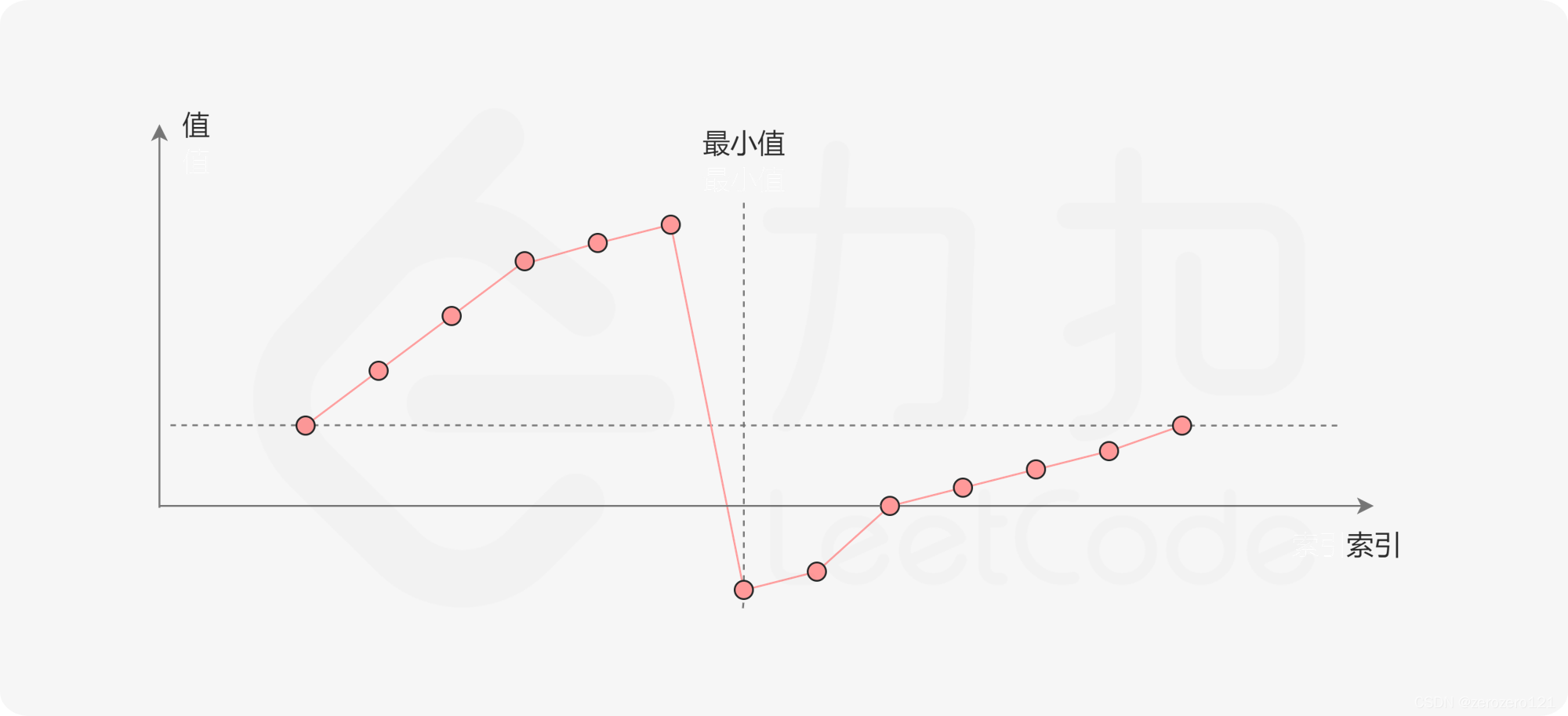
旋转数组可以分为左右两个部分,左右两个部分的序列都是区间严格递增的,而最小值必落在右边的区间。
因此我们可以判断此时mid在左右哪个区间,分两种情况。
- 如果
mid大于右区间right,说明mid在左半区,就将left移动到mid + 1,因为最小值不可能在左半区 - 如果
mid小于右区间right,如果mid在右半区,则当前mid有可能是最小值,此时将right移动到mid
代码实现:
public int findMin(int[] nums) {
int left = 0;
int right = nums.length - 1;
while(left < right) {
int mid = left + (right - left) / 2;
// 如果mid在左半区
if(nums[mid] > nums[right]) {
left = mid + 1;
// 如果mid在右半区
} else {
right = mid;
}
}
return nums[left];
}
(2)数组中的值可能相同
算法分析:
因此我们可以判断此时mid在左右哪个区间,分三种情况讨论。
- 如果
mid大于右区间right,说明当前mid在左半区,此时将left移动到mid + 1,因为最小值不可能在左半区 - 如果
mid小于等于右区间right,说明当前mid在右半区,则当前mid有可能是最小值,此时将right移动到mid - 如果
mid等于右区间right,即nums[mid] == nums[right],此时说明right的值可以被mid取代,所以右区间减一做缩容操作
代码实现:
public int findMin(int[] nums) {
int left = 0;
int right = nums.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
// 左半区
if(nums[mid] > nums[right]){
left = mid + 1;
// 右半区
} else if(nums[mid] < nums[right]) {
right = mid;
} else {
right--;
}
}
return nums[left];
}
2.查找指定值target
题目描述:
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
设计一个时间复杂度为 O(log n) 的解决方案。

(1)数组中的值各不相同
算法分析:
旋转数组可以分为左右两个部分,左右两个部分的序列都是区间严格递增的,分三种情况讨论。
-
当前
mid的值等于target,找到目标值,返回下标 -
当前
mid的值大于right,此时mid落在左半区,然后判断target是否比mid小,如果target在mid左边,就将right移动到mid-1,否则将left移动到mid+1 -
当前
mid的值小于right,此时mid落在右半区,然后判断target是否比mid大,如果target在mid右边,就将left移动到mid+1,否则将right移动到mid-1
代码实现:
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target) {
return mid;
}
// 左半区
if(nums[mid] > nums[right]) {
if(target >= nums[left] && target < nums[mid]) {
right = mid - 1;
} else {
left = mid + 1;
}
// 右半区
} else {
if(target <= nums[right] && target > nums[mid]) {
left = mid + 1;
} else {
right = mid - 1;
}
}
}
return -1;
}
(2)数组中的值可能相同
算法分析:
旋转数组可以分为左右两个部分,分三种情况讨论。
-
当前
mid的值等于target,找到目标值,返回下标 -
如果
mid等于右区间right和左区间left,即nums[mid] == nums[right] && nums[mid] == nums[left],此时说明right和left的值均可以被mid取代,所以左右区间各减一做缩容操作 -
当前
mid的值大于right,此时mid落在左半区,然后判断target是否比mid小,如果target在mid左边,就将right移动到mid-1,否则将left移动到mid+1 -
当前
mid的值小于或等于right,当mid==right,因为mid已经不等于left了,否则就满足了条件二,所以此时mid落在右半区,然后判断target是否比mid大,如果target在mid右边,就将left移动到mid+1,否则将right移动到mid-1
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target) {
return mid;
}
if(nums[mid] == nums[left] && nums[mid] == nums[right]) {
right--;
left++;
} else if(nums[mid] >= nums[left]) {
if(target >= nums[left] && target < nums[mid]) {
right = mid - 1;
} else {
left = mid + 1;
}
} else {
if(target <= nums[right] && target > nums[mid]) {
left = mid + 1;
} else {
right = mid - 1;
}
}
}
return -1;
}
