题目:
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
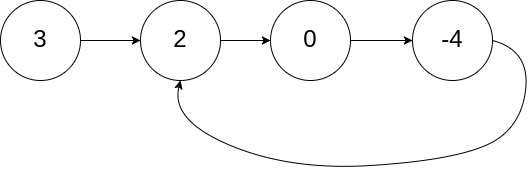
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/linked-list-cycle
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解决思路:
使用两个指针,一个慢的每次走一步,一个快的每次走两步.
如果两个指针相遇了,肯定有环,否则就没有环
证明:
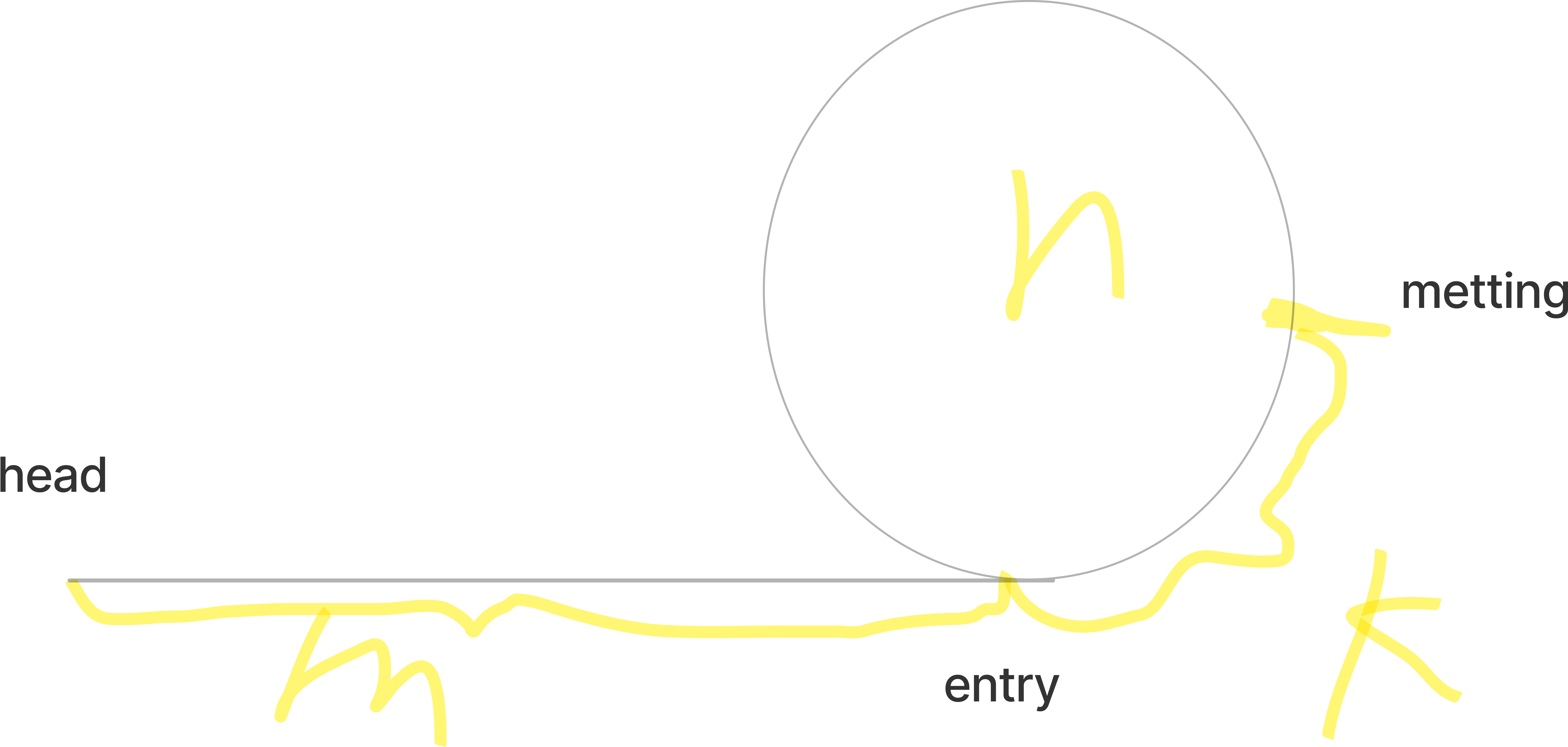
令: head=头节点; entry:环的入口处节点; meeting:相遇时所在的节点.
n=环的长度; m=head到entry的距离; k=entry到meeting的距离.
慢的每次走一步(速度为1),快的每次走两步(速度为2).同时出发,相遇时有:
slow 路程为: S1 = m + k + t1*n
fast 路程为 : S2 = m + k + t2*n
因为fast 速度是slow 的二倍,即
S2= 2*S1
m + k + t2*n = 2 *( m + k + t1*n)
化简得:
( t2 - 2 *t1) * n = m + k
也就是m+k 就是环的倍数
这个等式显然有解,所以会相遇.
下图为求解head 到 entry 的距离思路:

参考:
https://zhuanlan.zhihu.com/p/105269431
https://www.cnblogs.com/zywscq/p/10727079.html
代码:
public boolean hasCycle(ListNode head) {
if (head.next == null) {
return false;
}
ListNode slow,fast;
slow = fast = head;
while (slow != null && fast != null){
slow = slow.next;
fast = fast.next != null ? fast.next.next : null;
if (slow == fast){
return true;
}
}
return false;
}
