[数据结构与算法]大津法的C语言实现

大津法

大津法又叫最大类间方差法,由日本学者大津展之在1979年提出的对图像二值化高效算法.

对于一帧灰度图像,一个像素由八位0~255表示,单片机是很难实时处理这么大的数据的,我们需要通过一个阈值将其二值化,小于这个阈值的像素判定黑色,大于的判定白色.

摄像头视野内，最主要的颜色就是赛道白色和蓝布蓝色，对于总钻风获取的灰度图也可以通过灰度直方图来区分,下图是photoshop提取的灰度直方图,可以非常明显地看到两个峰,我们需要找到一个值(一般在两峰之间),使这个值两边间类方差最大.

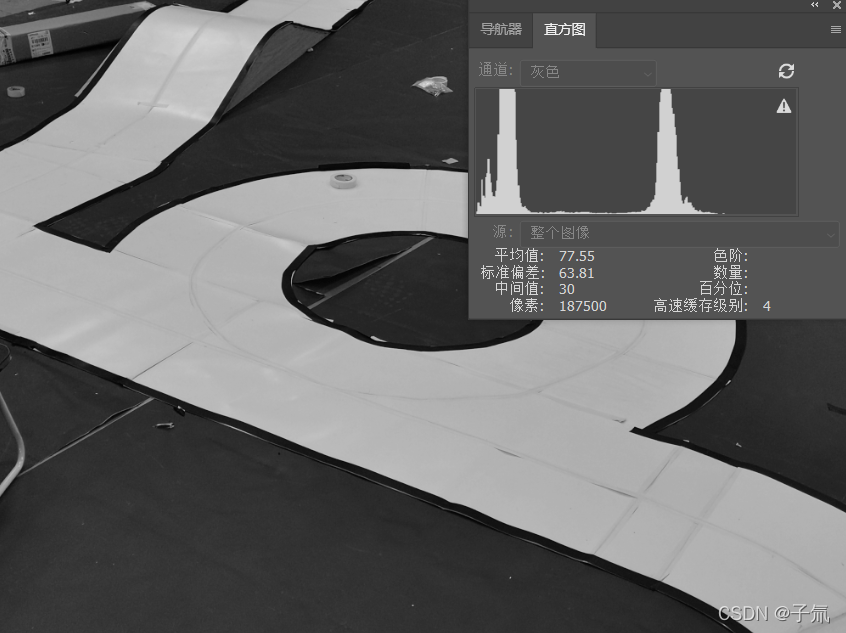
原理

将直方图在一阈值分割为两组,使这两组之间方差最大.

对一张图像

• $m$: 灰度值为$1～m$级
• $n_i$: 灰度值$i$的像素数量
• $N$: 像素总数 $N={\sum }_{i=0}^n{x}_i$
• $p_i$: 各级灰度概率 $p_i=\frac{n_i}{N}$

用一个灰度阈值$k$将像素分为前景$C_0=|1～k|$和背景$C_1=|k+1～m|$两组,得到

• ${\omega }_0$: 前景$C_0$组像素出现的概率 ${\omega }_0=\omega (k)={\sum }_{i=1}^k{p}_i$
• ${\mu }_0$: 前景$C_0$组灰度平均值 ${\mu }_0=\mu (k)=\frac{\mu (k)}{\omega (k)}={\sum }_{i=1}^k\frac{i?p_i}{{\omega }_0}$
• ${\omega }_1$: 背景$C_1$组像素出现的概率 ${\omega }_1=1?{\omega }_0={\sum }_{i=k+1}^m{p}_i$
• ${\mu }_1$: 背景$C_1$组灰度平均值 ${\mu }_1=\frac{\mu ?\mu (k)}{1?\omega (k)}={\sum }_{i=k+1}^m\frac{i?p_i}{{\omega }_1}$
• $\mu$: 整个图像灰度平均值 $\mu ={\omega }_0{\mu }_0+{\omega }_1{\mu }_1$
• ${\delta }^2$: 两组间方差 ${\delta }^2={\omega }_0({\mu }_0?\mu {)}^2+{\omega }_1({\mu }_1?\mu {)}^2={\omega }_0{\omega }_1({\mu }_1?{\mu }_0{)}^2$

我们需要做的是求出一个$k$值,使得两组间方差${\delta }^2$最大,这就是图像进行二值分割的阈值,可以得到最理想的效果.

实现

定义灰度直方图数组grayhist,灰度有16级,32级,64级三种级次,而灰度图一个像素用8位数据(0~255)表示,64级灰度即把256分为64级,故用嵌套for循环遍历整个图像,读取其值再除以4得到灰度值(右移2位),同时求总灰度值和像素数量,这里步长为形参step并传入10可节省计算量.

for~for~
temp_this_pixel = img[n] >> 2;
if (temp_this_pixel < 64)
    grayhist[temp_this_pixel]++;
gray_sum_all += temp_this_pixel;
px_sum_all++;

接下来用迭代法求取令两组间方差fCal_var最大的k值

for
    w0 = px_sum / px_sum_all;
    w1 = 1 - w0;
    u0 = gray_sum / px_sum;
    u1 = (gray_sum_all - gray_sum) / (px_sum_all - px_sum);
    fCal_var = w0 * w1 * (u0 - u1) * (u0 - u1);
// 找到使方差最大的k值
if (fCal_var > fTemp_maxvar)
    fTemp_maxvar = fCal_var;
    temp_best_th = k;

这样求得的$k$值是64灰度级次下的k,需要返回256灰度下的阈值return k*4.

这样得到的阈值可以用if和else来进行二值化了

if(temp >= threshold)
    bitmap = 1;
else
    bitmap = 0;

代码

int img_otsu(uint8_t *img, uint8_t img_v, uint8_t img_h)
{
    uint8_t grayhist[64] = {0}; //灰度直方图
    uint16_t px_sum_all = 0;             //像素点总数
    uint32_t gray_sum_all = 0;           //总灰度积分
    uint16_t px_sum = 0;                 //像素点数量
    uint32_t gray_sum = 0;               //灰度积分
	float fCal_var;

    //生成：1. 灰度直方图 2. 像素点总数 3. 总灰度积分
    for (int i = 0; i < img_v; i += 10)
    {
        for (int j = 0; j < img_h; j += 10)
        {
            temp_this_pixel = img[i * img_h + j] /4;
            grayhist[temp_this_pixel]++;
            gray_sum_all += temp_this_pixel;
            px_sum_all++;
        }
    }
    //迭代求得最大类间方差的阈值
    float fTemp_maxvar = 0;
    uint8_t temp_best_th = 0;
    uint8_t temp_this_pixel = 0;
    float u0, u1, w0, w1;
    for (uint8_t k = 0; k < 64; k++)
    {
        px_sum += grayhist[k];       //该灰度及以下的像素点数量
        gray_sum += k * grayhist[k]; //该灰度及以下的像素点的灰度和
        w0 = 1.0 * px_sum / px_sum_all;
        w1 = 1.0 - w0;
        u0 = 1.0 * gray_sum / px_sum;
        u1 = 1.0 * (gray_sum_all - gray_sum) / (px_sum_all - px_sum);
        fCal_var = w0 * w1 * (u0 - u1) * (u0 - u1);
        if (fCal_var > fTemp_maxvar)
        {
            fTemp_maxvar = fCal_var;
            temp_best_th = k;
        }
    }
    return temp_best_th  * 4;
}

超强干货来袭

云风专访：近40年码龄，通宵达旦的技术人生