[数据结构与算法]扩展欧几里得算法的讲解

扩展欧几里得算法：扩展欧几里得算法：对于正整数a, b，一定存在非零整数x, y，使得ax + by = gcd(a, b)。

求解x， y的过程：

设ax1+by1=gcd(a,b), bx2+(a%b)y2=gcd(b,a%b);
由gcd(a,b)=gcd(b,a%b),可得:
ax1+by1=bx2+(a%b)y2;
即:ax1+by1=bx2+(a-(a/b)*b)y2
? ? ? ? ? =ay2+bx2-(a/b)*by2;
即:ax1+by1=ay2 + b(x2-(a/b)*y2)
根据恒等定理,对应项相等，得:x1=y2; y1=x2-(a/b)*y2;
这样我们就得到了:x1，y1的值基于x2，y2，所以我们可以通过递归求解。

题目：

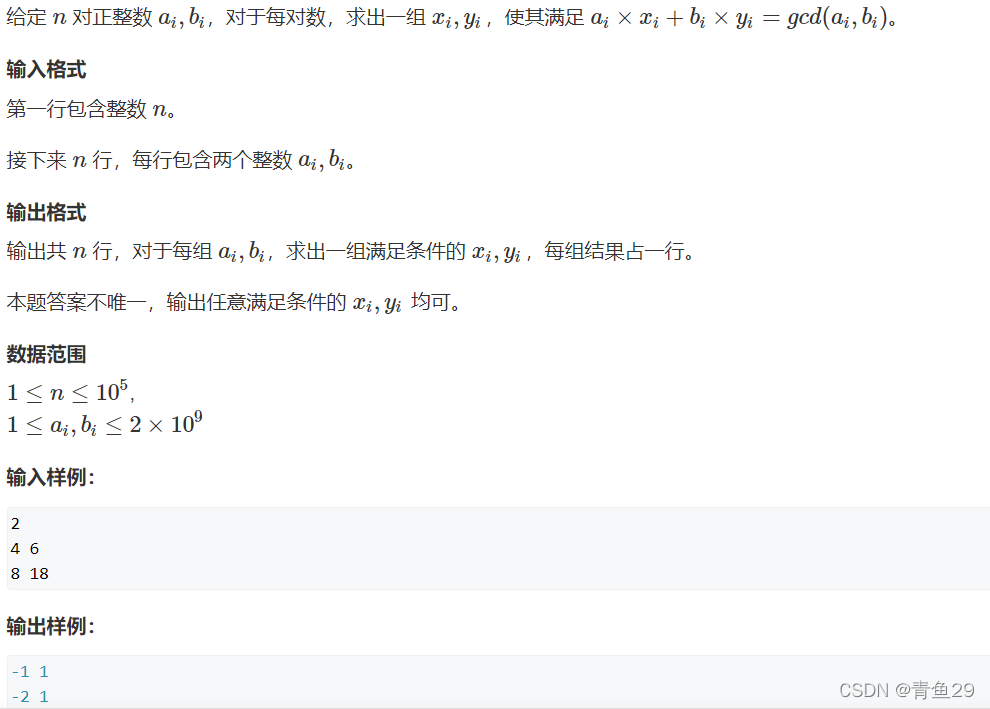
代码实现：

//扩展欧几里得算法：对于正整数a, b，一定存在非零整数x, y，使得ax + by = gcd(a, b)
//a 和 b的最大公约数就是a 和 b能凑出来的最小的正整数

#include <iostream>
using namespace std;

int exgcd(int a, int b, int& x, int& y)
{
    if(b == 0)
    {
        x = 1, y = 0;
        return a;
    }
    //注意欧几里得算法本就是一个递归过程
    //所以这里需要递归求解x， y
    int d =  exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}

int main()
{
    int n = 0;
    scanf("%d", &n);
    
    while (n --)
    {
        int a = 0, b = 0, x = 0, y = 0;
        scanf("%d%d", &a, &b);
        
        exgcd(a, b, x, y);
        printf("%d %d\n", x, y);
    }
    return 0;
}

超强干货来袭

云风专访：近40年码龄，通宵达旦的技术人生