[数据结构与算法] 2022年团体程序设计天梯赛-模拟赛

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 2022年团体程序设计天梯赛-模拟赛 -> 正文阅读

[数据结构与算法]2022年团体程序设计天梯赛-模拟赛

前面几个题比较简单，不加题解了，后面几个题目附上文字题解。
…实际上后面几个题解也写的比较简单，懒了…

ps: 代码大部分是比赛的时候写的，有几个题目写的比较搓，大佬见谅。

L1-1 自动编程 (5 分)

输出语句是每个程序员首先要掌握的语句。Python 的输出语句很简单，只要写一个 print(X) 即可，其中 X 是需要输出的内容。

本题就请你写一个自动编程机，对任何一个要输出的整数 N，给出输出这个整数的 Python 语句。

输入格式：

输入给出一个不超过 105 的正整数。

输出格式：

在一行中打印输出这个整数的 Python 语句，其中不包含任何空格。

输入样例：

输出样例：

print(520)

#include <iostream>
using namespace std;
int main()
{
    int x;
    cin >> x;
    printf("print(%d)", x);
    return 0;
}

L1-2 太神奇了 (5 分)

“告诉大家一个神奇的消息，太神奇了：明年全世界所有的人都同岁，全部都等于2022。明年的日子很特别，大概每1000年才会有一次。明年你的周岁年龄+你的出生年，每个人都是2022年。例如：你明年57加上1965年生的，加起来就是2022年。特别奇怪，连中外专家都无法解释！你计算一下，看看是不是2022。真是千年等一回呀！真准！转朋友圈，让大伙都算一下吧！”

据说这个“电子包浆”贴每年都会出现。本题就请你根据发贴人提到的周岁年龄和出生年，判断其发贴的时候是哪一年。

输入格式：

输入在第一行中给出两个正整数，即周岁年龄和出生年，其中年龄在 (0, 200) 区间内，出生年在 (1900, 2022) 区间内。

输出格式：

在一行中输出发贴年份。

输入样例：

57 1965

输出样例：

样例说明

因为贴子里说“明年全世界所有的人都同岁”，所以发贴是在今年，即 2021 年。

#include <iostream>
using namespace std;
int main()
{
    int x, y;
    cin >> x >> y;
    cout << x + y - 1;
    return 0;
}

L1-3 洛希极限 (10 分)

科幻电影《流浪地球》中一个重要的情节是地球距离木星太近时，大气开始被木星吸走，而随着不断接近地木“刚体洛希极限”，地球面临被彻底撕碎的危险。但实际上，这个计算是错误的。

洛希极限（Roche limit）是一个天体自身的引力与第二个天体造成的潮汐力相等时的距离。当两个天体的距离少于洛希极限，天体就会倾向碎散，继而成为第二个天体的环。它以首位计算这个极限的人爱德华·洛希命名。（摘自百度百科）

大天体密度与小天体的密度的比值开 3 次方后，再乘以大天体的半径以及一个倍数（流体对应的倍数是 2.455，刚体对应的倍数是 1.26），就是洛希极限的值。例如木星与地球的密度比值开 3 次方是 0.622，如果假设地球是流体，那么洛希极限就是 0.622×2.455=1.52701 倍木星半径；但地球是刚体，对应的洛希极限是 0.622×1.26=0.78372 倍木星半径，这个距离比木星半径小，即只有当地球位于木星内部的时候才会被撕碎，换言之，就是地球不可能被撕碎。

本题就请你判断一个小天体会不会被一个大天体撕碎。

输入格式：

输入在一行中给出 3 个数字，依次为：大天体密度与小天体的密度的比值开 3 次方后计算出的值（≤1）、小天体的属性（0 表示流体、1 表示刚体）、两个天体的距离与大天体半径的比值（>1 但不超过 10）。

输出格式：

在一行中首先输出小天体的洛希极限与大天体半径的比值（输出小数点后2位）；随后空一格；最后输出 ^_^ 如果小天体不会被撕碎，否则输出 T_T。

输入样例 1：

0.622 0 1.4

输出样例 1：

1.53 T_T

输入样例 2：

0.622 1 1.4

输出样例 2：

0.78 ^_^

#include <iostream>
using namespace std;
int main()
{
    double a, b, c;
    int t;
    cin >> a >> t >> b;
    if (t)
        c = a * 1.26;
    else
        c = a * 2.455;
    printf("%.2f %s", c, (c > b ? "T_T" : "^_^"));
    return 0;
}

L1-4 吃鱼还是吃肉 (10 分)

肉.JPG

国家给出了 8 岁男宝宝的标准身高为 130 厘米、标准体重为 27 公斤；8 岁女宝宝的标准身高为 129 厘米、标准体重为 25 公斤。

现在你要根据小宝宝的身高体重，给出补充营养的建议。

输入格式：

输入在第一行给出一个不超过 10 的正整数 N，随后 N 行，每行给出一位宝宝的身体数据：

性别 身高 体重

其中性别是 1 表示男生，0 表示女生。身高和体重都是不超过 200 的正整数。

输出格式：

对于每一位宝宝，在一行中给出你的建议：

如果太矮了，输出：duo chi yu!（多吃鱼）；
如果太瘦了，输出：duo chi rou!（多吃肉）；
如果正标准，输出：wan mei!（完美）；
如果太高了，输出：ni li hai!（你厉害）；
如果太胖了，输出：shao chi rou!（少吃肉）。

先评价身高，再评价体重。两句话之间要有 1 个空格。

输入样例：

输出样例：

ni li hai! duo chi rou!
duo chi yu! wan mei!
wan mei! shao chi rou!
duo chi yu! shao chi rou!

L1-5 不变初心数 (15 分)

不变初心数是指这样一种特别的数，它分别乘 2、3、4、5、6、7、8、9 时，所得乘积各位数之和却不变。例如 18 就是这样的数：18 的 2 倍是 36，3+6=9；18 的 3 倍是 54，5+4=9；…… 18 的 9 倍是 162，1+6+2=9。对于 18 而言，9 就是它的初心。本题要求你判断任一个给定的数是否有不变的初心。

输入格式：

输入在第一行中给出一个正整数 N（≤ 100）。随后 N 行，每行给出一个不超过 105 的正整数。

输出格式：

对每个给定的数字，如果它有不变的初心，就在一行中输出它的初心；否则输出 NO。

输入样例：

输出样例：

9
NO
36
NO

题解

简单的模拟题。

取出来某数的每一位也很容易，之后来个循环判断一遍就行。

#include <iostream>
using namespace std;
int f(int x)
{
    int s = 0;
    while (x)
    {
        s += x % 10;
        x /= 10;
    }
    return s;
}
int main()
{
    int N;
    cin >> N;
    while (N--)
    {
        int x;
        cin >> x;
        int q = x;
        int s = f(x);
        int i;
        for (i = 2; i < 10; i++)
        {
            x = q * i;
            if (s != f(x))
            {
                cout << "NO\n";
                break;
            }
        }
        if (i == 10)
            cout << s << endl;
    }
    return 0;
}

L1-6 字母串 (15 分)

英语老师要求学生按照如下规则写一串字母：

如果写了某个大写字母，下一个就必须写同个字母的小写，或者写字母表中下一个字母的大写；
如果写了某个小写字母，下一个就必须写同个字母的大写，或者写字母表中前一个字母的小写；
当然也可以什么都不写，就结束这个字母串。

例如 aAaABCDdcbBC 就是一个合法的字母串；而 dEFfeFGhI 就是非法的。注意 a 没有前一个字母， Z 也没有下一个字母。

现在面对全班学生交上来的作业，老师请你写个程序自动批改。

输入格式：

输入在第一行给出一个不超过 100 的正整数 N。随后 N 行，每行给出一位学生的作业，即仅由英文字母组成的非空字母串，长度不超过 2×106。

输出格式：

对每位学生的作业，如果正确就在一行中输出 Y，否则输出 N。

输入样例：

2
aAaABCDdcbBC
dEFfeFGhI

输出样例：

Y
N

题解

比上一题复杂一些的模拟题，不过实际上本题的规则很明显，判断也比较好写。

如果写了某个大写字母**（isupper判断），下一个就必须写同个字母的小写（转成小写tolower），或者写字母表中下一个字母的大写（+1）**；
如果写了某个小写字母**（islower判断），下一个就必须写同个字母的大写（转成大写toupper），或者写字母表中前一个字母的小写（+1）**
最后判断是否是最后一个字符**（最后一个字符无需判断）**

#include <iostream>
using namespace std;
int main()
{
    int N;
    cin >> N;
    while (N--)
    {
        string s;
        cin >> s;
        int f = 0;
        for (int i = 0; i < (int)s.size(); i++)
        {
            if (isupper(s[i]))
            {
                if (i == (int)s.size() - 1)
                    break;
                
                    if (tolower(s[i]) == s[i + 1] || s[i] + 1 == s[i + 1])
                        continue;
                    else
                    {
                        f = 1;
                        break;
                    }
                
            }
            else
            {
                if (i == (int)s.size() - 1)
                    break;
                
                    if (toupper(s[i]) == s[i + 1] || s[i] - 1 == s[i + 1])
                    {
                        continue;
                    }
                    else
                    {
                        f = 1;
                        break;
                    }
            }
        }
        if(f)
            cout << "N\n";
        else 
            cout << "Y\n";
    }
    return 0;
}

L1-7 矩阵列平移 (20 分)

给定一个 n×n 的整数矩阵。对任一给定的正整数 k<n，我们将矩阵的偶数列的元素整体向下依次平移 1、……、k、1、……、k、…… 个位置，平移空出的位置用整数 x 补。你需要计算出结果矩阵的每一行元素的和。

输入格式：

输入第一行给出 3 个正整数：n（<100）、k（<n）、x（<100），分别如题面所述。

接下来 n 行，每行给出 n 个不超过 100 的正整数，为矩阵元素的值。数字间以空格分隔。

输出格式：

在一行中输出平移后第 1 到 n 行元素的和。数字间以 1 个空格分隔，行首尾不得有多余空格。

输入样例：

7 2 99
11 87 23 67 20 75 89
37 94 27 91 63 50 11
44 38 50 26 40 26 24
73 85 63 28 62 18 68
15 83 27 97 88 25 43
23 78 98 20 30 81 99
77 36 48 59 25 34 22

输出样例：

440 399 369 421 302 386 428

样例解读

需要平移的是第 2、4、6 列。给定 k=2，应该将这三列顺次整体向下平移 1、2、1 位（如果有更多列，就应该按照 1、2、1、2 …… 这个规律顺次向下平移），顶端的空位用 99 来填充。平移后的矩阵变成：

11 99 23 99 20 99 89
37 87 27 99 63 75 11
44 94 50 67 40 50 24
73 38 63 91 62 26 68
15 85 27 26 88 18 43
23 83 98 28 30 25 99
77 78 48 97 25 81 22

题解

这个题之前没见过，比赛的时候还真被卡了一下，虽然也是简单题。

题目大意：奇数列不同，偶数列依次向下平移 1、……、k、1、……、k、…… ，空位置用x填充。

主要是注意一下平移的时候，k的变化：可以令k从0开始，每移动完一列k++，并且k%=原K，这样计算的新行就是 k + 1 + i

#include <iostream>
using namespace std;
// 原数组
int a[200][200];
// 转换之后的数组
int b[200][200];

int main()
{
    int N, k, x;
    cin >> N >> k >> x;
    for (int i = 1; i <= N; i++)
        for (int j = 1; j <= N; j++)
            cin >> a[i][j];
    // 因为k是变动的，故多定义一个
    int kt = 0;
    for (int j = 1; j <= N; j++)
    {
        // 偶数列平移
        if (j % 2 == 0)
        {
            for (int i = 1; i <= N; i++)
            {
                // kt从0开始，故多加个1（从0开始，kt%k的时候会方便一些）
                int now = kt + 1 + i;
                b[now][j] = a[i][j];
            }
            kt++;
            kt %= k;
        }
        else
            for (int i = 1; i <= N; i++)
                b[i][j] = a[i][j];
    }
    for (int i = 1; i <= N; i++)
    {
        int s = 0;
        for (int j = 1; j <= N; j++)
        {

            if (b[i][j] == 0)
                s += x;
            else
                s += b[i][j];
        }
        if (i != 1)
            cout << ' ';
        cout << s;
    }
    return 0;
}

L1-8 均是素数 (20 分)

在给定的区间 [m,n] 内，是否存在素数 p、q、r（p<q<r），使得 pq+r、q**r+p、r**p+q 均是素数？

输入格式：

输入给出区间的两个端点 0<m<n≤1000，其间以空格分隔。

输出格式：

在一行中输出满足条件的素数三元组的个数。

输入样例：

1 35

输出样例：

样例解读

满足条件的 10 组解为：

2, 3, 5
2, 3, 7
2, 3, 13
2, 3, 17
2, 5, 7
2, 5, 13
2, 5, 19
2, 5, 31
2, 7, 23
2, 13, 17

题解

比赛时写的代码，略挫，但胜在好理解。

题目大意：有三个素数，并且他们进行乘运算和加运算之后的结果也是素数，求这三个数。

范围比较小，三层循环也不会出现超时，直接开三个循环判断就行。注意的是，内层循环不要从1开始，会重复。

#include <iostream>
#include <cmath>
using namespace std;
int s[11000];
int f(int x)
{
    if (x <= 1)
        return false;
    for (int i = 2; i <= sqrt(x); i++)
    {
        if (x % i == 0)
            return false;
    }
    return true;
}
int main()
{
    int a, b;
    cin >> a >> b;
    // 标记一下[a,b]范围内的素数
    // 实际上写的时候我担心超时，但是...素数筛法我还忘了...实际上没事，不记录这个应该也行.
    for (int i = a; i <= b; i++)
        s[i] = f(i);
    int ans = 0;
    for (int p = a; p <= b; p++)
        if (s[p])
            for (int q = p + 1; q <= b; q++)
                if (s[q])
                    for (int r = q + 1; r <= b; r++)
                        if (s[r])
                        {
                            int t = p * q + r;
                            int w = q * r + p;
                            int e = r * p + q;
                            if (f(t) && f(w) && f(e))
                                ans++;
                        }
    cout << ans;
    return 0;
}

L2-1 盲盒包装流水线 (25 分)

众所周知，PAT 有 9 枚徽章，分别对应青铜、白银、黄金、白金、钻石、大师、王者、大圣、天神这 9 个段位，只有成绩非常优秀的考生才有资格获得刻有自己名字的徽章。现在，PAT 制作了徽章的小型纪念版，要制成盲盒给大家玩了！

下图是一条盲盒包装流水线的示意图。首先徽章通过进货口被压入货栈里，空盒在履带上从左向右传送。每次从货栈里弹出一枚徽章，进入打包机，装入一只空盒，打包后继续向右边传送。当货栈为空时，打包机会暂停，等待下一批徽章压入货栈。

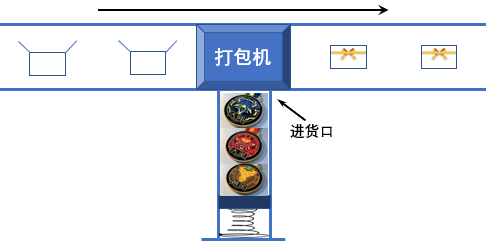
每只盒子都有一个编号，小拼姐姐手里有进入流水线的空盒编号顺序表，也有每一批送往货栈的徽章顺序表，这样她其实可以知道每只盒子里装了哪种徽章。有些小朋友收到了盲盒，就想在拆封前问无所不知的小拼姐姐，盒子里的徽章是哪一种。但是因为盲盒总量有 105 这么多，小拼姐姐可记不住每只盒子里装的是什么，于是你就被请来写个程序帮小拼姐姐回复这种信息。

输入格式：

输入第一行给出 2 个正整数，分别为盲盒总量 N（≤105）和货栈容量 S（≤100）。接下来一行给出 N 只盒子的编号，编号由 5 位数字组成，给出的顺序是空盒进入传送带的顺序。随后 N/S（保证是整数）行，每行给出一批 S 枚徽章的类型，为 1-9 的数字，给出的顺序是从进货口入栈的顺序。

再下面给出一个正整数 K（≤104），为查询次数。随后 K 行，每行给出一个 5 位编号。

输出格式：

对每个查询编号，在一行中输出该盒子中装的徽章类型。如果编号是错误的，则在一行中输出 Wrong Number。

输入样例：

10 5
00132 10093 92001 23333 66666 88888 09009 34658 82750 69251
1 2 3 4 5
9 8 7 6 1
5
66666
88888
69251
55555
10093

输出样例：

1
1
9
Wrong Number
4

题解

题目大意：

给一堆箱子编号，然后N/S批徽章，并且这批徽章的入出的方式是栈。

需要解决的问题就是一批箱子和一批徽章之间的对应、一个箱子和一个徽章的对应。

#include <iostream>
#include <stack>
#include <vector>
#include <map>
#include <set>
using namespace std;
const int n = 1e5 + 10;
int a[n];
//  徽章进入传送带的顺序
// 一共是N/S批，每一批的徽章都是先进后出，是一个栈
vector<stack<int>> v;
int main()
{
    int N, S;
    cin >> N >> S;
    for (int i = 0; i < N; i++)
        cin >> a[i];
    int pi = N / S;
    v.resize(pi + 10);
    for (int i = 0; i < pi; i++)
        for (int j = 0; j < S; j++)
        {
            int x;
            cin >> x;
            v[i].push(x);
        }
    // 将编号和徽章对应起来，同时也可以判断编号是否错误
    map<int, int> rap;
    int index = 0;
    // 一批有S个，一批一批的看
    for (int i = 0; i < N; i += S, index++)
    {
        for (int j = i; j < i + S; j++)
        {
            // 栈的操作
            rap[a[j]] = v[index].top();
            v[index].pop();
        }
    }

    int k;
    cin >> k;
    while (k--)
    {
        int x;
        cin >> x;
        if (rap.count(x) == 0)
            cout << "Wrong Number\n";
        else
            cout << rap[x] << endl;
    }
    return 0;
}

L2-2 点赞狂魔 (25 分)

微博上有个“点赞”功能，你可以为你喜欢的博文点个赞表示支持。每篇博文都有一些刻画其特性的标签，而你点赞的博文的类型，也间接刻画了你的特性。然而有这么一种人，他们会通过给自己看到的一切内容点赞来狂刷存在感，这种人就被称为“点赞狂魔”。他们点赞的标签非常分散，无法体现出明显的特性。本题就要求你写个程序，通过统计每个人点赞的不同标签的数量，找出前3名点赞狂魔。

输入格式：

输入在第一行给出一个正整数N（≤100），是待统计的用户数。随后N行，每行列出一位用户的点赞标签。格式为“Name K F1?F**K”，其中Name是不超过8个英文小写字母的非空用户名，1≤K≤1000，F**i（i=1,?,K）是特性标签的编号，我们将所有特性标签从 1 到 107 编号。数字间以空格分隔。

输出格式：

统计每个人点赞的不同标签的数量，找出数量最大的前3名，在一行中顺序输出他们的用户名,其间以1个空格分隔,且行末不得有多余空格。如果有并列，则输出标签出现次数平均值最小的那个，题目保证这样的用户没有并列。若不足3人，则用-补齐缺失，例如mike jenny -就表示只有2人。

输入样例：

5
bob 11 101 102 103 104 105 106 107 108 108 107 107
peter 8 1 2 3 4 3 2 5 1
chris 12 1 2 3 4 5 6 7 8 9 1 2 3
john 10 8 7 6 5 4 3 2 1 7 5
jack 9 6 7 8 9 10 11 12 13 14

输出样例：

jack chris john

题解

set
此题很明显需要使用set
点赞数量的求解比较简单
主要的是排序方法，题目说的很~~
主排序，实现也简单
主要是说的“标签出现次数平均值最小的”
= 总点赞数 / 真实数量

#include <iostream>
#include <vector>
#include <set>
#include <algorithm>
using namespace std;
struct node
{
    string id;
    int cnt;
    double x;
};
int main()
{
    vector<node> v;
    int N;
    cin >> N;
    while (N--)
    {
        string s;
        cin >> s;
        set<int> ret;
        int m;
        cin >> m;
        for (int i = 0; i < m; i++)
        {
            int x;
            cin >> x;
            ret.insert(x);
        }
        int len = ret.size();
        v.push_back({s, len, 1.0 * m / len});
    }
    sort(v.begin(), v.end(), [](auto &e1, auto &e2) { return (e1.cnt == e2.cnt ? (e1.x < e2.x) : (e1.cnt > e2.cnt)); });
    int i;

    for ( i = 0; i < v.size() && i < 3; i++)
    {
        if (i != 0)
            cout << " ";
        cout << v[i].id;
    }
    while (i++ < 3)
        cout << " -";
    return 0;
}

L2-3 浪漫侧影 (25 分)

“侧影”就是从左侧或者右侧去观察物体所看到的内容。例如上图中男生的侧影是从他右侧看过去的样子，叫“右视图”；女生的侧影是从她左侧看过去的样子，叫“左视图”。

520 这个日子还在打比赛的你，也就抱着一棵二叉树左看看右看看了……

我们将二叉树的“侧影”定义为从一侧能看到的所有结点从上到下形成的序列。例如下图这棵二叉树，其右视图就是 { 1, 2, 3, 4, 5 }，左视图就是 { 1, 6, 7, 8, 5 }。

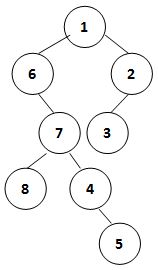
于是让我们首先通过一棵二叉树的中序遍历序列和后序遍历序列构建出一棵树，然后你要输出这棵树的左视图和右视图。

输入格式：

输入第一行给出一个正整数 N (≤20)，为树中的结点个数。随后在两行中先后给出树的中序遍历和后序遍历序列。树中所有键值都不相同，其数值大小无关紧要，都不超过 int 的范围。

输出格式：

第一行输出右视图，第二行输出左视图，格式如样例所示。

输入样例：

8
6 8 7 4 5 1 3 2
8 5 4 7 6 3 2 1

输出样例：

R: 1 2 3 4 5
L: 1 6 7 8 5

题解

先序+中序和后序+中序 传送门

只要把树建起来，就简单了。

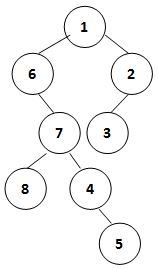
注意看这个图，只要把树建起来，并且得到树的层次遍历，那么结果：

左：每一层的第一个数 level[i][0];

右：每一层的最后一个数 level[i].back();

至于层次遍历，可以写一个bfs求出来，当然也可以在建树的过程中求出来

有一个问题比较有意思

最初我们写的代码，总是出现段错误，我们发现是建树的时候的问题，已经我们都是用的这个方法来建，这次为啥不行了呢？

区别是在区间的计算上面：

出现段错误的建树代码：

void build(int inL, int inR, int postL, int postR, int Level)
{
    if (inL > inR || postL > postR)
        return;
    // 记录总层数
    maxt = max(maxt, Level);
    int index = 0;
    while (in[index] != pt[postR])
    {
        index++;
    }
    int len = inR - index;
    level[Level].push_back(pt[postR]);
    build(inL, index - 1, postL, postR - 1 - len, Level + 1);
    build(index + 1, inR, postR - len, postR - 1, Level + 1);
}

AC代码

void build(int inL, int inR, int postL, int postR, int Level)
{
    if (inL > inR || postL > postR)
        return;
    maxt = max(maxt, Level);
    int index = 0;
    while (in[index + inL] != pt[postR])
    {
        index++;
    }
    // int len = inR - index;
    level[Level].push_back(pt[postR]);
    build(inL, inL + index - 1, postL, postL + index - 1, Level + 1);
    build(inL + index + 1, inR, postL + index, postR - 1, Level + 1);
}

/*
    U?ェ?*U
    mommo重返江湖
    U?ェ?*U
*/
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
vector<int> level[100];
int in[100];
int pt[100];
int N;
int maxt = 0;
void build(int inL, int inR, int postL, int postR, int Level)
{
    if (inL > inR || postL > postR)
        return;
    maxt = max(maxt, Level);
    int index = 0;
    while (in[index + inL] != pt[postR])
    {
        index++;
    }
    // int len = inR - index;
    level[Level].push_back(pt[postR]);
    build(inL, inL + index - 1, postL, postL + index - 1, Level + 1);
    build(inL + index + 1, inR, postL + index, postR - 1, Level + 1);
}
int main()
{
    cin >> N;
    for (int i = 0; i < N; i++)
        scanf("%d", &in[i]);
    for (int i = 0; i < N; i++)
        scanf("%d", &pt[i]);
    build(0, N - 1, 0, N - 1, 0);

    cout << "R:";
    for (int i = 0; i <= maxt; i++)
        cout << ' ' << level[i].back();
    cout << endl;
    cout << "L:";
    for (int i = 0; i <= maxt; i++)
        cout << " " << level[i][0];
    return 0;
}

L2-4 哲哲打游戏 (25 分)

哲哲是一位硬核游戏玩家。最近一款名叫《达诺达诺》的新游戏刚刚上市，哲哲自然要快速攻略游戏，守护硬核游戏玩家的一切！

为简化模型，我们不妨假设游戏有 N 个剧情点，通过游戏里不同的操作或选择可以从某个剧情点去往另外一个剧情点。此外，游戏还设置了一些存档，在某个剧情点可以将玩家的游戏进度保存在一个档位上，读取存档后可以回到剧情点，重新进行操作或者选择，到达不同的剧情点。

为了追踪硬核游戏玩家哲哲的攻略进度，你打算写一个程序来完成这个工作。假设你已经知道了游戏的全部剧情点和流程，以及哲哲的游戏操作，请你输出哲哲的游戏进度。

输入格式：

输入第一行是两个正整数 N 和 M (1≤N,M≤105)，表示总共有 N 个剧情点，哲哲有 M 个游戏操作。

接下来的 N 行，每行对应一个剧情点的发展设定。第 i 行的第一个数字是 K**i，表示剧情点 i 通过一些操作或选择能去往下面 K**i 个剧情点；接下来有 K**i 个数字，第 k 个数字表示做第 k 个操作或选择可以去往的剧情点编号。

最后有 M 行，每行第一个数字是 0、1 或 2，分别表示：

0 表示哲哲做出了某个操作或选择，后面紧接着一个数字 j，表示哲哲在当前剧情点做出了第 j 个选择。我们保证哲哲的选择永远是合法的。
1 表示哲哲进行了一次存档，后面紧接着是一个数字 j，表示存档放在了第 j 个档位上。
2 表示哲哲进行了一次读取存档的操作，后面紧接着是一个数字 j，表示读取了放在第 j 个位置的存档。

约定：所有操作或选择以及剧情点编号都从 1 号开始。存档的档位不超过 100 个，编号也从 1 开始。游戏默认从 1 号剧情点开始。总的选项数（即 ∑K**i）不超过 106。

输出格式：

对于每个 1（即存档）操作，在一行中输出存档的剧情点编号。

最后一行输出哲哲最后到达的剧情点编号。

输入样例：

输出样例：

题解

首先是记录剧情点的信息，用vector存图的方式就行。

几个操作实现也比较简单。

#include <iostream>
#include <vector>
using namespace std;
const int n = 1e5 + 10;
vector<int> v[n];
int main()
{
    int N, M;
    cin >> N >> M;
    for (int i = 1; i <= N; i++)
    {
        int k;
        cin >> k;
        while (k--)
        {
            int x;
            cin >> x;
            v[i].push_back(x);
        }
    }
    int cun[n] = {0};
    int i = 1;
    while (M--)
    {
        int op, j;
        cin >> op >> j;
        if (op == 0)
        {
            i = v[i][j - 1];
        }
        else if (op == 1)
        {
            cun[j] = i;
            // cout << "---";
            cout << i << endl;
        }
        else
        {
            i = cun[j];
        }
    }
    cout << i;
    return 0;
}