[数据结构与算法]AtCoder Beginner Contest 248

AtCoder Beginner Contest 248

A - Lacked Number

题意：

给出10个数字，输出0~9中未出现的那个数字。

思路：

统计数字出现情况即可。

时间复杂度：

$O(1)$

AC代码：

#include<bits/stdc++.h>
typedef long long ll;
const int N = 2e5+10,M = 2e5+10,INF = 0x3f3f3f3f,mod = 32768;


int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    int cnt[10] = {0};
    std::string s;
    std::cin>>s;
    for(auto c : s)cnt[c-'0']++;
    for(int i = 0 ; i < 10 ; i++)if(!cnt[i])std::cout<<i;
    return 0;
}

B - Slimes

题意：

给定$A,B,K$三个数字,每次操作可以使$A=A?K$,输出$A\ge B$的最小次数

思路：

直接模拟即可。

时间复杂度：

$O(\frac{B}{AK})$

AC代码：

#include<bits/stdc++.h>
typedef long long ll;
const int N = 2e5+10,M = 2e5+10,INF = 0x3f3f3f3f,mod = 32768;


int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    ll a,b,k;
    std::cin>>a>>b>>k;
    int cnt = 0;
    while(b > a)cnt++,a *= k;
    std::cout<<cnt;
    return 0;
}

C - Dice Sum

题意：

现要求找到一个长度为$N$的序列，对于其中的每一个元素，满足如下要求：

1. $1\le A_i\le M$
2. ${\sum }_{i=1}^N{A}_i\le K$

询问满足要求的序列个数。

思路：

考虑动态规划

设有$dp[N][K]$：

1. 第一维表示当前序列长度
2. 第二维表示当前序列的和
3. 数组的值表示方案数

枚举所有长度以及序列和，进行状态转移即可。

转移方程：

for(int i = 1 ; i <= n ; i++)
        for(int j = 1 ; j <= m ; j++)
            for(int o = i + j - 1; o <= k ; o++)
            {
                dp[i][o] = (dp[i][o] + dp[i-1][o-j])%mod;
            }

时间复杂度：

$O(NK)$

AC代码：

#include<bits/stdc++.h>
typedef long long ll;
const int N = 60,M = 2e5+10,INF = 0x3f3f3f3f,mod = 998244353;

ll dp[N][N*N];

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    int n,m,k;
    std::cin>>n>>m>>k;
    dp[0][0] = 1;
    for(int i = 1 ; i <= n ; i++)
        for(int j = 1 ; j <= m ; j++)
            for(int o = i + j - 1; o <= k ; o++)
            {
                dp[i][o] = (dp[i][o] + dp[i-1][o-j])%mod;
            }
    ll sum = 0;
    for(int i = n ; i<= k ; i++)sum = (sum + dp[n][i])%mod;
    std::cout<<sum;
    return 0;
}

D - Range Count Query

题意：

给定一个长度为$n$的序列，和$q$个询问，询问格式如下：

给定$L,R,X$,要求输出序列中$L$到$R$区间内值为$X的个数。

思路：

因为$1\le A_i\le N$，所以我们可以用一个数组，把每一个数字的所有下标分别存起来，然后用二分解决询问即可。

时间复杂度：

$O(qlogn)$

AC代码：

#include<bits/stdc++.h>
typedef long long ll;
const int N = 2e5+10,M = 2e5+10,INF = 0x3f3f3f3f,mod = 998244353;

std::vector<int> v[N];

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    int n,q;
    std::cin>>n;
    for(int i = 1 ; i <= n ; i++)
    {
        int x;
        std::cin>>x;
        v[x].push_back(i);
    }
    std::cin>>q;
    while(q--)
    {
        int l,r,x;
        std::cin>>l>>r>>x;
        auto it1 = std::lower_bound(v[x].begin(),v[x].end(),l);
        if(it1==v[x].end())
        {
            std::cout<<0<<'\n';
            continue;
        }
        auto it2 = std::upper_bound(v[x].begin(),v[x].end(),r);
        if(it2==v[x].begin())
        {
            std::cout<<0<<'\n';
            continue;
        }
        it2--;
        std::cout<<(it2-it1+1)<<'\n';
    }
    return 0;
}

E - K-colinear Line

题意：

在坐标平面内存在$N$个点，每个点的坐标为$(X_i,Y_i)$，询问存在多少条不同的直线，穿过至少$K$个点。

思路：

因为两点可以确定一条直线，而且点数$N\le 300$，所以可以进行如下处理：

1. 两两枚举所有的点
2. 在确定完一条直线后，枚举所有的点判断这条直线穿过了多少点

三个点在一条直线上，显然有$AC=kAB$

$\frac{y_3?y_2}{x_3?x_2}=\frac{y_3?y_1}{x_3?x_1}?(y_3?y_2)(x_3?x_1)=(x_3?x_2)(y_3?y_1)$

将所有满足条件的直线统计出来即可。

时间复杂度：

$O(n^3)$

AC代码：

#include<bits/stdc++.h>
typedef long long ll;
const int N = 310,M = 2e5+10,INF = 0x3f3f3f3f,mod = 998244353;
struct Node{
    ll x,y;
}a[N];
bool book[N][N];

bool OK(Node x,Node y,Node z)
{
    return (z.y-y.y)*(z.x-x.x)==(z.y-x.y)*(z.x-y.x);
}

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    int ans = 0;
    int n,k;
    std::cin>>n>>k;
    if(k==1)
    {
        std::cout<<"Infinity";
        return 0;
    }
    for(int i = 1 ; i <= n ; i++)std::cin>>a[i].x>>a[i].y;
    for(int i = 1 ; i < n ; i++)
        for(int j = i + 1 ; j <= n ; j++)
            if(!book[i][j])
            {
                int cnt = 2;
                std::vector<int> b;
                for(int o = 1 ; o <= n ; o++)
                {
                    if(o == i || o == j)continue;
                    if(OK(a[i],a[j],a[o]))
                    {
                        cnt++;
                        b.push_back(o);
                    }
                }
                b.push_back(i);
                b.push_back(j);
                for(auto x : b)
                    for(auto y : b)book[x][y] = true;
                if(cnt >= k)ans++;
            }
    std::cout<<ans;
    return 0;
}

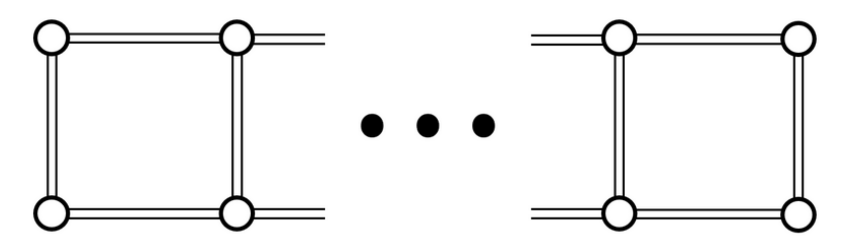
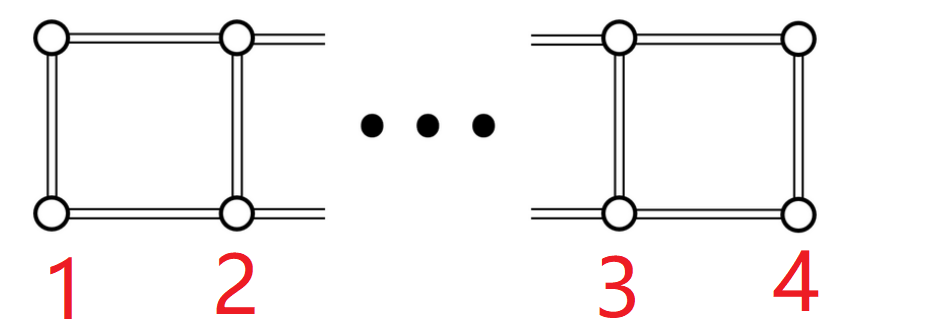
F - Keep Connect

题意：

给出这样的一个连通图，对于每一个$i(1\le i\le n?1)$，输出删除$i$条边并且仍然保持连通性的方案数。

思路：

考虑动态规划

设有$dp[i][j][2]$:

1. $i$表示前$i$组点
2. $j$表示删除的边数
3. 第三维记录的是第$i$组点之间的连通性(第$i$组的两个点当前能否连通)
4. 数组值表示方案数
   

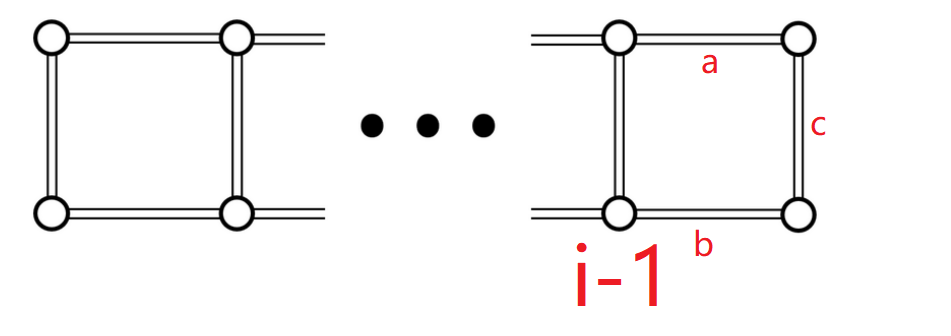
我们用三个$bool$值$a,b,c$来代表三条边，表示这条边是否删除。

1. 那么当第$i?1$组点是不连通的时候，显然是要保证$a,b$两条边都相连，否则整张图必然失去连通性。
2. 当第$i?1$组点是连通的时候，我们只需要保证$a,b$有一条边是连通的即可，如果$a,b,c$三边中相连了至少两条边，那么就可以保证第$i$组点是连通的。
   

有转移方程

if(!k)
{
    if(!a||!b)continue;
    dp[i+1][j+1-c][c] = (dp[i+1][j+1-dp[i][j][k])%Mod;
}
else
{
    if(!a&&!b)continue;
    dp[i+1][j+3-a-b-c][(a+b+c)>=2] = [j+3-a-b-c][(a+b+c)>=2] + dp[i%Mod;
}

时间复杂度：

$O(n^2)$

AC代码：

#include<bits/stdc++.h>
typedef long long ll;
const int N = 3010,M = 2e5+10,INF = 0x3f3f3f3f,mod = 998244353;

ll dp[N][N][2];

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    dp[1][0][1] = dp[1][1][0] = 1;
    int n;
    ll Mod;
    std::cin>>n>>Mod;
    for(int i = 1 ; i < n ; i++)
        for(int j = 0 ; j <= n ; j++)
            for(int k = 0 ; k < 2 ; k++)
                if(dp[i][j][k])
                    for(int a = 0 ; a < 2 ; a++)
                        for(int b = 0 ; b < 2 ; b++)
                            for(int c = 0 ; c < 2 ; c++)
                            {
                               if(!k)
                               {
                                   if(!a||!b)continue;
                                   dp[i+1][j+1-c][c] = (dp[i+1][j+1-c][c] + dp[i][j][k])%Mod;
                               }
                               else
                               {
                                   if(!a&&!b)continue;
                                   dp[i+1][j+3-a-b-c][(a+b+c)>=2] = (dp[i+1][j+3-a-b-c][(a+b+c)>=2] + dp[i][j][k])%Mod;
                               }
                            }
    for(int i = 1 ; i < n ; i++)std::cout<<dp[n][i][1]<<' ';
    return 0;
}

Ex - Beautiful Subsequences

题意：

给定一个长度为$n$的全排列,询问满足如下条件的区间个数：

• $1\le L\le R\le N$
• $max(P_L,\dots ,P_R)?min(P_L,\dots ,P_R)\le R?L+K$

思路：

线段树+单调栈：

1. 线段树：我们先固定一个$R$,然后尝试去维护一个序列，这个序列中的第$i$个点记录的值为$max(P_i,\dots ,P_R)?min(P_i,\dots ,P_R)?R+i$，如果这个值$val\le K$,那么这个点所代表的区间就是一个合法区间，此外，因为这个序列是全排列，所以不难发现$val$不会是负数。我们用线段树去维护这一段区间，区间内记录$val$的最小值，并且记录下$val+1,val+2,\dots ,val+k$的点的个数。
   然后就可以通过根节点的信息推知答案。

2. 单调栈：我们可以通过单调栈动态的确定区间最值，确定完最值以后通过线段树区间修改即可。

时间复杂度：

$O(NKlogN)$

AC代码：

#include<bits/stdc++.h>
typedef long long ll;
const int N = 150000,M = 2e5+10,INF = 0x3f3f3f3f,mod = 998244353;
struct Node{
    int l,r;
    int val,add,cnt[4];
}tr[N*4];
int w[N],k;

void pushup(int u)
{
    tr[u].val = std::min(tr[u<<1].val,tr[u<<1|1].val);
    for(int i = 0 ; i <= k ; i++)
    {
        tr[u].cnt[i] = 0;
        int temp = tr[u].val - tr[u<<1].val + i;
        if(temp >= 0)tr[u].cnt[i] += tr[u<<1].cnt[temp];
        temp = tr[u].val - tr[u<<1|1].val + i;
        if(temp >= 0)tr[u].cnt[i] += tr[u<<1|1].cnt[temp];
    }
}

void pushdown(int u)
{
    if(tr[u].add)
    {
        tr[u<<1].val += tr[u].add;
        tr[u<<1|1].val += tr[u].add;
        tr[u<<1].add += tr[u].add;
        tr[u<<1|1].add += tr[u].add;
        tr[u].add = 0;
    }
}

void build(int u,int l,int r)
{
    if(l==r)
    {
        tr[u] = {l,r};
        tr[u].cnt[0] = 1;
        tr[u].val = INF;
    }
    else
    {
        tr[u] = {l,r};
        int mid = l + r >> 1;
        build(u<<1,l,mid),build(u<<1|1,mid+1,r);
    }
}

void modify(int u,int l,int r,int v)
{
    if(l > r)return;
    if(tr[u].l >= l && tr[u].r <= r)
    {
        tr[u].val += v;
        tr[u].add += v;
    }
    else
    {
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if(l <= mid)modify(u<<1,l,r,v);
        if(r > mid)modify(u<<1|1,l,r,v);
        pushup(u);
    }
}

int main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);
    int n;
    std::cin>>n>>k;
    for(int i = 1 ; i <= n ; i++)std::cin>>w[i];
    build(1,1,n);
    std::stack<std::pair<std::pair<int,int>,int>> stk1,stk2;
    ll ans = 0;
    for(int i = 1 ; i <= n ; i++)
    {
        modify(1,i,i,-INF);
        modify(1,1,i-1,-1);
        int x1 = i,x2 = i;
        while(!stk1.empty())
        {
            if(w[i] < stk1.top().second)
            {
                modify(1,stk1.top().first.first,stk1.top().first.second,stk1.top().second);
                x1 = stk1.top().first.first;
                stk1.pop();
            }
            else break;
        }
        while(!stk2.empty())
        {
            if(w[i] > stk2.top().second)
            {
                modify(1,stk2.top().first.first,stk2.top().first.second,-stk2.top().second);
                x2 = stk2.top().first.first;
                stk2.pop();
            }
            else break;
        }
        stk1.push({{x1,i},w[i]});
        stk2.push({{x2,i},w[i]});
        modify(1,x1,i,-w[i]);
        modify(1,x2,i,w[i]);
        for(int c = 0 ; c <= k ; c++)
            if(tr[1].val + c <= k)ans += tr[1].cnt[c];
    }
    std::cout<<ans;
    return 0;
}

欢迎访问个人博客https://skynesser.github.io/

创作挑战赛

新人创作奖励来咯，坚持创作打卡瓜分现金大奖