文章目录
前言
??????动态规划算法
??????本文会大致聊一下动态规划算法的思想和及其特征,并通过一些示例来进行说明和算法实现。
??????一、斐波那契数列作为示例描述了自顶而下和自底而上算法的实现
??????二、凑零钱问题的几种实现
??????三、通过动态规划求最短路径问题
??????希望读者据此可以对DP有一个基本的了解。特别是在示例中仔细体会它的三个特点,无后效性、最优子结构和子问题重叠。
动态规划介绍:
??????以下摘自百度百科:
??????动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样,但它们具有相同的填表格式。
??????适用动态规划的问题必须满足最优化原理和无后效性。
??????1、最优子结构性质
??????最优子结构指的是,问题的最优解包含子问题的最优解。反过来就是,可以通过子问题的最优解,推导出问题的最优解。
??????2、无后效性
??????在推导当前阶段状态的时候,只需要考虑上一阶段的状态,不必关心上一阶段状态是如何推导出来的;如果当前阶段状态已经确定,那它就不会受到之后阶段的决策影响。换句话说,每个状态都是过去历史的一个完整总结。这就是无后向性,又称为无后效性。
??????3、子问题的重叠性
??????因为不同的决策序列在到达某个相同的阶段时可能会产生重复的状态,所以动态规划的关键在于解决冗余,这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术,它在实现的过程中,不得不存储产生过程中的各种状态,所以它的空间复杂度要大于其他的算法。选择动态规划算法是因为动态规划算法在空间上可以承受,而搜索算法在时间上却无法承受,所以我们舍空间而取时间。
??????4、自顶而下和自底而上
??????简单地来说,自底而上:从最小的子问题开始求解,每次求解之后就保存起来,如果求解后面有需要,直接读取即可,不需要再次求解子问题了。自顶而下:从大问题开始求解,因为大问题肯定没法直接求解,所以需要依赖一些子问题的求解,将从大问题到某个小问题之间的所有问题依次求解,然后保存起来,如果后面有需要,直接读取即可。
示例1:斐波那契数列
??????斐波那契数列比较简单,假定数列为:f(0)=1,f(1)=1,f(2)=2… 那么求 f(n) 的算法参考如下:
自顶而下
//自顶而下:
public int f(int n){
int[] dp=new int[n+1]; //dp数组,或称为备忘录
dp[0]=dp[1]=1;
return solve(n,dp);
}
public int solve(int n,int[] dp){
if(dp[n]!=0)
return dp[n];
//先保存结果,在返回其值
dp[n]=solve(n-1,dp)+solve(n-2,dp);
return dp[n];
}
自底而上
//自底而上:
public int f(int n){
if(n==1||n==0)
return 1;
int[] dp=new int[n+1];
dp[0]=dp[1]=1;
for(int i=2;i<=n;i++)
dp[i]=dp[i-1]+dp[i-2];
return dp[n];
}
??????由于当前状态只和之前两个状态有关,所以不需要用长度为 n 的数组来保存所有的状态,只需要存储之前两个状态即可,所以自底而上算法的空间复杂度最小可为 O(1) 。
示例2:凑零钱问题
??????问题描述可参考文章:https://www.zhihu.com/question/23995189 ,这篇文章中对动态规划的描述非常不错,接下来的内容都是在该文章的基础上给出自己的一些延申,该文章中的所有想法在下面都会一一进行实现。
??????凑零钱问题:有不同面值的硬币,每种硬币的数量不限,如何能够用最少的硬币数量凑出某一个给定面值数额,不同硬币的面值用 coins 数组表示,比如 coins[0] 表示 1 元硬币,coins[1] 表示 5 元硬币,coin[2] 表示 11 元硬币,目标数额用 target 来表示,假设 tartget 为 15 元。那么如何得到最少的硬币数量能够表示出 15 呢?
??????如果选择 1 元硬币,那么凑出 15 的最少硬币数量等于凑出 15-1 的最少硬币数量加一
??????如果选择 5 元硬币,那么凑出 15 的最少硬币数量等于凑出 15-5 的最少硬币数量加一
??????如果选择 11 元硬币,那么凑出 15 的最少硬币数量等于凑出 15-11 的最少硬币数量加一
??????即,凑出 n 的硬币数量等于凑出 m 的硬币数量加一,据此,可以用 f(n) 来表示凑出 n 的最少硬币数量,那么能得到公式:f(n)= min{ f(n-1),f(n-5),f(n-11) } +1
??????无后效性指的是,比如一旦计算出 f(9),那么它的值就不会改变,不管在计算任何一个 f(n) 时。
??????最优子结构指的是,求 f(n) 的问题可以通过求一些子问题 f(n-1),f(n-5),f(n-11) 的答案得到。
??????子问题重叠指的是,在上面的求解过程中,有不少子问题的答案需要被重复使用(这一点要是很难理解的话,可以通过上面斐波那契数列的实现来理解),这也是 DP 需要建立备忘录的原因,否则会造成重复计算。
??????注意:下面代码假设给定不同种类的硬币可以凑出任意面值。
1、实现状态转移:
//思路实现:
public int solution(int[] coins, int target) {
for (int coin : coins)
if (target == coin)
return 1;
int ans = Integer.MAX_VALUE;
for (int coin : coins) {
if (target > coin)
ans = Math.min(ans, solution(coins, target - coin) + 1);
}
return ans;
}
2.1、DP 自顶而下(记忆化搜索):
//这道题的分析思路适合采用自顶而下的方法。
public int solution(int[] coins,int target){
int[] dp=new int[target+1];//这里数组的大小应该为 max(target,max(coins[0]...coins[lenth]))+1;
for(int i=0;i<coins.length;i++)
dp[coins[i]]=1;
return solve(dp,coins,target);
}
public int solve(int[] dp, int[] coins, int target){
if(target==0)
return 0;
if(dp[target]!=0)
return dp[target];
int tmp=Integer.MAX_VALUE;
for(int i=0;i<coins.length;i++){
if(target>coins[i])
tmp=Math.min(tmp, solve(dp,coins,target-coins[i])+1);
}
dp[target]=tmp;
return dp[target];
}
2.2、DP 自底而上(按顺序递推):
public int solution(int[] coins, int target) {
/* 写法1:
int[] dp=new int[target+1];
for(int coin:coins)
dp[coin]=1;
for(int i=1;i<=target;i++){
if(dp[i]==0){
int max=Integer.MAX_VALUE;
for(int coin:coins)
if(i>coin)
max=Math.min(max,dp[i-coin]+1);
dp[i]=max;
}
}
return dp[target];
*/
//写法2
int[] dp=new int[target+1];
dp[0]=0;
for(int i=1;i<=target;i++){
int max=Integer.MAX_VALUE;
for(int coin:coins){
if(i>=coin){
max=Math.min(max,dp[i-coin]+1);
}
}
dp[i]=max;
}
return dp[target];
}
3、DP 的另一种思路:
??????之前的不管是自顶而下还是自底而上,是一种思路的两种不同实现方式,就像状态转移方程那样:f(n)= min{ f(n-1),f(n-5),f(n-11) } +1,n 总是由 n-1、n-5 和 n-11 得到。
??????还有一种思路是:假设 f(n) 已经计算出来,那么从 f(n) 出发,我们又能推出哪些结果?答案是:f(n+1)、f(n+5) 和 f(n+11) 的可能值,假如一系列点都可以推出在 f(n+1) 处的值,那么我们选择其中的最小值作为 f(n+1) 的最小值。这种实现思路在参考文章中被称为 push 型,相应的之前的实现思路被称为 pull 型。参考代码如下:
public int solution(int[] coins, int target) {
int[] dp=new int[target+1];
Arrays.fill(dp,Integer.MAX_VALUE);//初始化为最大的int值
dp[0]=0;
for(int i=0;i<=target;i++){
//在 i 处,对所有 i+coins[j] 处元素进行赋值
for(int j=0;j<coins.length;j++){
if(i+coins[j]<=target)
dp[i+coins[j]]=Math.min(dp[i]+1,dp[i+coins[j]]);
}
}
return dp[target];
}
4、顺便打印出凑零钱的具体方案
??????下面代码在计算出凑出 target 所需要的最少硬币数量之外,还打印出具体的方案-如何凑出。
public void solution(int[] coins, int target) {
List<String> l=new ArrayList<>();
int[] dp=new int[target+1];
dp[0]=0;
l.add(new String(""));//target为0时,用空字符串表示
String tmp=null;
for(int i=1;i<=target;i++){
int max=Integer.MAX_VALUE;
for(int coin:coins){
if(i>=coin){
int change=max;//change表示max是否发生变化
max=Math.min(max,dp[i-coin]+1);
if(max!=change){//如果有变化就表示找到了更少的解决方案(比如在i=5时)
tmp=new String(l.get(i-coin)+" "+coin);
}
}
}
dp[i]=max;
l.add(tmp);
System.out.println("凑出 "+i+" 的最少硬币数: "+dp[i]+" "+l.get(i));
}
}
示例3:动态规划求DAG中的最短路径
??????问题给定一个城市的地图,所有的道路都是单行道,而且不会构成环。每条道路都有过路费,问您从S点到T点花费的最少费用。如下图:
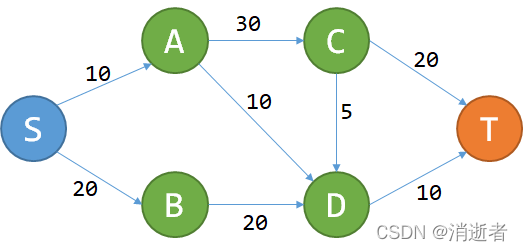
??????和凑零钱问题类似,令 f(T) 表示从 S 到 T 的最少费用,能够轻易看出求 f(T) 等效于求得 f?+20 和 f(D)+10 中的最小值,f? 等效于 f(A)+30,f(D) 等效于 f(A)+10、f?+5 和 f(B)+20 中的最小值 … 。所以能推出:
??????f(n)=min { f? + e(r,n) } ,其中 e(r,n) 表示从 r 点到 n 点的费用,r 表示所有能到达 n 的点。
算法实现
??????代码实现如下:
import java.util.*;
public class Tests {
public int minCost(int[][] edge,int nodeNum) {
int[] dp=new int[nodeNum];
dp[0]=0;//起点到自身的距离为0.
for(int i=1;i<nodeNum;i++){
int max=Integer.MAX_VALUE;
for(int j=0;j<nodeNum;j++){
if(edge[j][i]!=0){
max=Math.min(max,dp[j]+edge[j][i]);
}
}
dp[i]=max;
}
return dp[nodeNum-1];
}
public static void main(String[] args) {
Tests t = new Tests();
//这里的结点序列是经过拓扑排序之后的结果。在矩阵中可以看出所有元素均在右上方。
char[] node=new char[]{'S','A','B','C','D','T'};//顶点序列
List<int []> e=new ArrayList<>();//边上的信息
e.add(new int[]{0,1,10});
e.add(new int[]{0,2,20});
e.add(new int[]{1,3,30});
e.add(new int[]{1,4,10});
e.add(new int[]{2,4,20});
e.add(new int[]{3,4,5});
e.add(new int[]{3,5,20});
e.add(new int[]{4,5,10});
int nodeNum=node.length,edgeNum=e.size();
int[][] edge=new int[nodeNum][nodeNum];//构建邻接矩阵
for(int[] triple:e)
edge[triple[0]][triple[1]]=triple[2];
int ans= t.minCost(edge,nodeNum);//计算从'S' -> 'T' 的最少费用。
System.out.println("从S到T的最少费用:"+ans);
}
}
??????务必注意:上面的顶点序列是经过拓扑排序之后的结果。因为只有这样,才能采用动态规划来解决该问题,原因在于它给出了状态转移的方向,并且满足无后效性。
??????若是只给定一个DAG,求最短路径的时候需要采用Dijkstra算法,因为需要不断更新每个顶点的信息,因为从起点到每个顶点的最短路径 f(n) 是不断变化的。关于Dijkstra算法求最短路径可以参考之前写的文章:https://blog.csdn.net/Little_ant_/article/details/104291049
??????所以采用动态规划求最短路径时需要对图先做拓扑排序,不然此问题就不能才用 DP 来做。拓扑排序给出了图中的方向信息,这也是进行状态转移的一个必要条件,只有这样才能满足 DP 的三个特点最优子结构,无后效性以及子问题重叠性。
问题延申
??????那么,下面给出用 DP 求一个有向图中的最短路径算法,供读者参考,它可以求得图中任意两点之间的最短路径,注意在 minCost 方法中的一些细节,它和上面有点不一样,其中的 tp 方法用来对图进行拓扑排序,拓扑排序思想和实现可参考之前写的文章:https://blog.csdn.net/Little_ant_/article/details/104282371。
import java.util.*;
public class Tests {
public int minCost(int[][] edge,int start,int end) {
if(start>end)
return -1;
Map<Integer,Integer> dp=new HashMap<>();
dp.put(start,0);
for(int i=start+1;i<=end;i++){//从start+1开始,这是由拓扑排序的顺序决定的
int max=Integer.MAX_VALUE;
for(int j=start;j<i;j++){
if(edge[j][i]!=0){
max=Math.min(max,dp.get(j)+edge[j][i]);
}
}
if(max==Integer.MAX_VALUE)//如果某一个中间结点不能到达,那么end结点也就不能到达了。
return -1;
dp.put(i,max);
}
return dp.get(end)==null?-1:dp.get(end);
}
public String[] tp(String[] node,int[][] edge){
String[] ans=new String[node.length];
int[] inDegree=new int[node.length];//保存每个顶点的入度
int count=0;
for(int i=0;i<edge.length;i++){
count=0;
for(int j=0;j<edge.length;j++){
if(edge[j][i]!=0)
count++;
}
inDegree[i]=count;
}
Queue<Integer> que=new LinkedList<>();//保存入度为0结点的下标。
for(int i=0;i<inDegree.length;i++)
if(inDegree[i]==0)
que.offer(i);
count=0;//判断是否有环
while(!que.isEmpty()){
int tmp=que.poll();
ans[count]=node[tmp];
count++;
for(int i=0;i<edge.length;i++){
if(edge[tmp][i]!=0){
inDegree[i]--;
if(inDegree[i]==0)
que.offer(i);
}
}
}
if(count!=node.length)
return null;//此时由于有环的存在(一个环中的所有结点的入度都无法为0),程序提前退出,count小于结点数。
return ans;
}
public static void main(String[] args) {
Tests t = new Tests();
//给定任意一个图,node表示顶点,relations表示边上的权重,求任意两点之间的最短路径
String[] node=new String[]{"S","C","T","A","B","D"};
Map<String[],Integer> relations=new HashMap<>();
relations.put(new String[]{"S","A"},10);
relations.put(new String[]{"S","B"},20);
relations.put(new String[]{"A","C"},30);
relations.put(new String[]{"A","D"},10);
relations.put(new String[]{"B","D"},20);
relations.put(new String[]{"C","D"},5);
relations.put(new String[]{"C","T"},20);
relations.put(new String[]{"D","T"},10);
Map<String,Integer> nodeVsIndex=new HashMap<>();//建立顶点和下标的关系,方便后面建立邻接矩阵
for(int i=0;i<node.length;i++){
nodeVsIndex.put(node[i],i);
}
int[][] edge=new int[node.length][node.length];//建立邻接矩阵
for(String[] s:relations.keySet()){
int i=nodeVsIndex.get(s[0]),j=nodeVsIndex.get(s[1]);
edge[i][j]=relations.get(s);
}
//求拓扑排序 (在动态规划状态转移时给定一个可行方向)
String[] re=t.tp(node,edge);//得到一个新的顶点序列 re={S,A,B,C,D,T}
//由于顶点序列发生改变,所以构建一个新的edge矩阵。
for(int i=0;i<re.length;i++){
nodeVsIndex.put(re[i],i);
}
edge=new int[node.length][node.length];
for(String[] s:relations.keySet()){
int i=nodeVsIndex.get(s[0]),j=nodeVsIndex.get(s[1]);
edge[i][j]=relations.get(s);
}
//计算从 re[0] 到其他结点的最短路径
for(String s:re){
System.out.println(re[0]+"-> "+s+": "+t.minCost(edge,0,nodeVsIndex.get(s)));
}
}
}
示例4:求最长上升子序列(LIS)
??????问题描述:给定长度为 L 的序列 a,从 a 中抽取出一个子序列,这个子序列需要单调递增。问最长的上升子序列(LIS)的长度。e.g. 1,5,3,4,6,9,7,8的 LIS 为1,3,4,6,7,8,长度为6。
??????长度为 L 的序列的 LIS 长度和长度从 1 到 L-1 (不包含最后一个值)子序列的 LIS 长度有关。这个问题的状态描述为 f(n) :表示序列从 0 到下标为 n 的 LIS 长度,f(n) 的值和 f(1)…f(n-1) 有关。
??????那么对于 f(1) 到 f(n-1),如果 a[n] > a[i],那么 f(n) 可以暂定为 f(i)+1;如果 a[n]<= a[i],那么 f(n) 可以暂定为 f(i)。这样,f(n) 取所有可能值之间的最大值。参考算法如下:
public int solution(int[] a) {
//f(n)=max{f(<n),f(>n)}
int[] dp=new int[a.length];
dp[0]=1;
for(int i=1;i<a.length;i++){
//计算 dp[i] 的值
int max=-1;
for(int j=0;j<i;j++){
if(a[i]>a[j])
max=Math.max(max,dp[j]+1);
else
max=Math.max(max,dp[j]);
}
dp[i]=max;
}
return dp[a.length-1];
}
?????? 时间复杂度为 O(n2)。
总结
??????完
