开玩笑的,我一个月刷不完
1. 两数之和(easy)

不要给我说什么哈希查找,我不懂。看到题,啪一下就想到了两层暴力循环,注意很快哈。
1. 暴力枚举
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
vector<int>& num=nums;
for(int i=0;i<num.size();i++)
{
for(int j=1;j<num.size();j++)
{
if(num[i]+num[j]==target&&i!=j)//for (int j = i + 1; j < n; ++j)
{
return{i,j};
}
}
}
return{};
}
};这种双循环时间复杂度为n方
2. 哈希表
// 哈希表(集合),用来记录每个字符是否出现过
// 哈希表的散列技术是指在记录的存储位置和它的关键字之间建立一个确定的对应关系f,使每一个关键字都对应一个存储位置
思路:
快速查找某个元素采用哈希查找,采用unordered_map,这种一个key对应一个value的容器;
首先对数组进行遍历,在第i次遍历中,都去找target-nums[i]这个数是否存在;
如果再遍历一遍查找就是暴力枚举的办法,而采用哈希表查找就是哈希表法;
这是一种边赋值边查找的方式,注意不是从原数组中查找,而是从哈希表中查找:
注意要定义一个哈希表的迭代器it来返回下标。
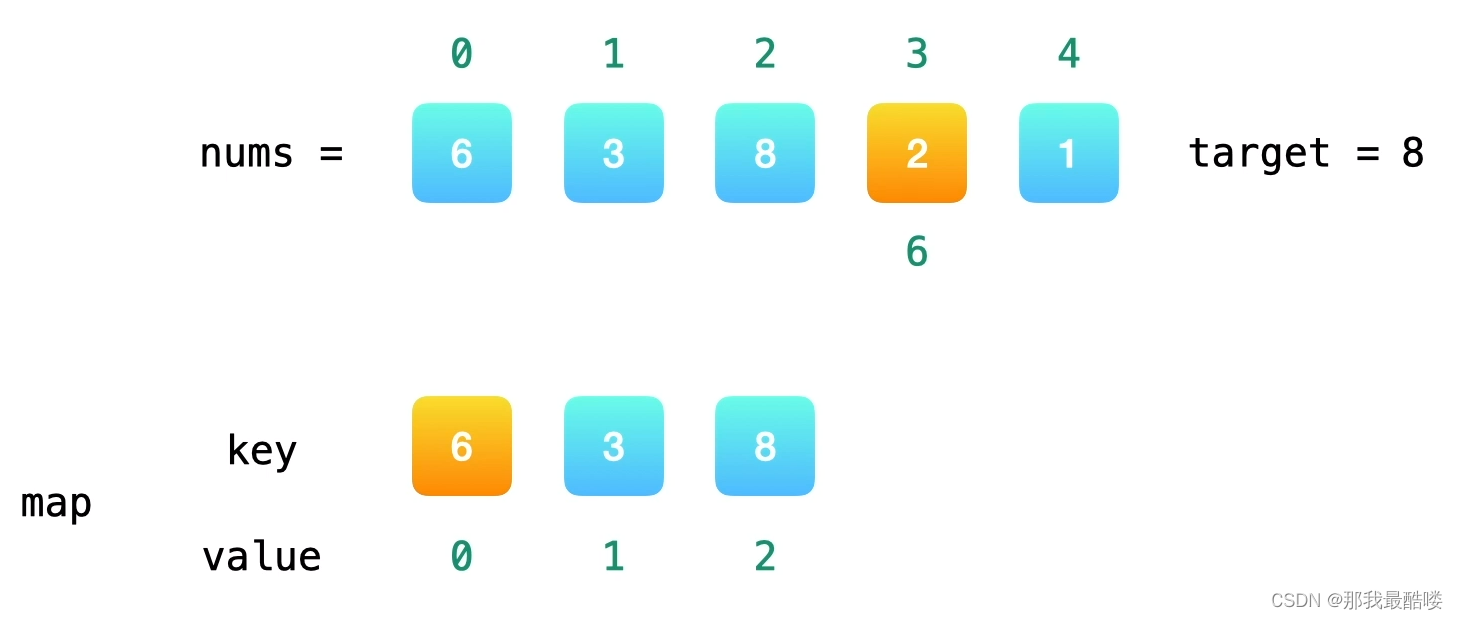
Eg:target=8:
nums[0]=6,需要找2,哈希表中没有,则存入key为nums[0],value为其在数组中的下标值0;nums[1]=3,需要找7,哈希表中没有,则存入key为nums[1],value为其在数组中的下标值1;nums[2]=8,需要找0,哈希表中没有,则存入key为nums[2],value为其在数组中的下标值2;nums[3]=2,需要找6,哈希表中有,则输出key为6时对应的value,即为其在数组中的下标;
class?Solution?{
public:
????vector<int>?twoSum(vector<int>&?nums,?int?target)?{
????????unordered_map<int,?int>?hashtable;
????????for?(int?i?=?0;?i?<?nums.size();?++i)?{
????????????auto?it?=?hashtable.find(target?-?nums[i]);
????????????if?(it?!=?hashtable.end())?{
????????????????return?{it->second,?i};
????????????}
????????????hashtable[nums[i]]?=?i;
????????}
????????return?{};
????}
};class?Solution?{
public:
????vector<int>?twoSum(vector<int>&?nums,?int?target)?{
//unordered_map<first_type,second_type>
//无序哈希表提供一种一个key对应一个value,用于快速查找
????????unordered_map<int,?int>?hashtable;
????????for?(int?i?=?0;?i?<?nums.size();?++i)?{
//采用find函数查找是否有value: “目标值减去当前nums[i]”
????????????auto?it?=?hashtable.find(target?-?nums[i]);
//如果it在没到达末尾之前找到,则返回it所对应的value和i,it->second表示it迭代器指向的value。
????????????if?(it?!=?hashtable.end())?{//这是判断哈希表是否查找到常用方式
????????????????return?{it->second,?i};
????????????}
//下标i是hash值,nums[i]是key值,通过key(nums[i])值找到value(i),返回i
//将?nums[i]?插入到哈希表中,即可保证不会让?x?和自己匹配。
//即边赋值边进行查找,为了避免重复值,因此实在循环之后才进行传值
//因为是要返回下标i,所以在哈希表中存入key=nums[i],value=i。
//就是通过需要找到的 “目标值减去当前nums[i]”值 找下标值i.
????????????hashtable[nums[i]]?=?i;
????????}
????????return?{};
????}
};时间复杂度和空间复杂度均为n。?
2. 两数相加(mid)
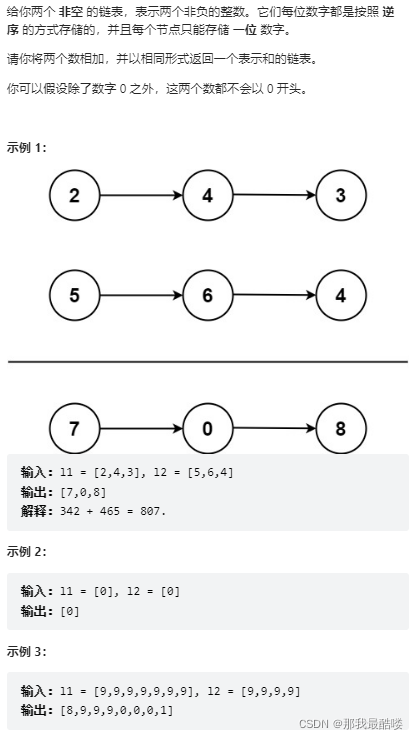
思路:?
首先创建一个新的链表,头结点指针和尾结点指针;
进入循环从前往后挨个就两个链表上此结点位置的和,不要忘了进位;
head为空时,创建新的节点赋值为sum%10,这样即使有进位也能赋值正确;
新链表不为空时,tail后面new新结点,并赋值sum%10,tail始终指向尾部节点;
在计算每一个结点尤其是尾结点时时都不能忘了进位;
如果一个链表结束了,要把另一个链表加到结束为止。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution{
public:
ListNode* addTwoNumbers(ListNode* l1,ListNode* l2)
{
ListNode *head=nullptr,*tail=nullptr;
int carry=0;
while(l1||l2)
{
int n1 = l1? l1->val : 0;
int n2 = l2? l2->val : 0;
int sum = n1 + n2 + carry;
if(!head){
head = tail = new ListNode(sum%10);
}
else{
tail->next=new ListNode(sum%10);
tail=tail->next;
}
carry=sum/10;
if(l1){
l1=l1->next;
}
if(l2){
l2=l2->next;
}
}
if(carry>0)
{
tail->next=new ListNode(carry);
}
return head;
}
};/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution{
public:
ListNode* addTwoNumbers(ListNode* l1,ListNode* l2)
{
ListNode *head=nullptr,*tail=nullptr;
//head,tail分别用来指到新链表的头结点和尾结点
int carry=0;//进位
while(l1||l2)//l1或l2没有遍历完则继续
{
//从链表前面开始逐位相加
//使用3目运算符是为了考虑某一个链表遍历完的情况,直接赋值0
int n1 = l1? l1->val : 0;
int n2 = l2? l2->val : 0;
int sum = n1 + n2 + carry;
if(!head){
head = tail = new ListNode(sum%10);
//一开始head为空,开辟head,tail空间,初始化
}
else{
tail->next=new ListNode(sum%10);
tail=tail->next;
}
carry=sum/10;//大于10则进位
//链表节点不为空则指向next
if(l1){
l1=l1->next;
}
if(l2){
l2=l2->next;
}
}
if(carry>0)//遍历完成后依然有进位
{
tail->next=new ListNode(carry);
}
return head;
}
};?3. 无重复字符的最长子串(mid)

最长不重复子串,本质上还是查找。采用哈希表是查找单个元素较快的方式;
在此题中采用unordered_set容器:
//set是按照特定顺序存储惟一元素的容器。
//无序集是不按特定顺序存储惟一元素的容器,允许根据元素的值快速检索单个元素
//与set容器相比,unordered_set容器通过 键 访问单个元素的速度更快,但它们通常在通过元素的子集进行范围迭代时效率较低
//unordered_set内部解决冲突采用的是链地址法
滑动窗口思路:
如果我们依次递增地枚举子串的起始位置,那么子串的结束位置也是递增的!因为假设我们选择字符串中的第 i 个字符作为起始位置,并且得到了不包含重复字符的最长子串的结束位置为 rk?。那么当我们选择第 i+1 个字符作为起始位置时,首先从 i+1 到 rk的字符显然是不重复的,并且由于少了原本的第 i 个字符,我们可以尝试继续增大 rk,直到右侧出现了重复字符为止。
这样一来,我们就可以使用「滑动窗口」来解决这个问题了:
我们使用两个指针表示字符串中的某个子串(或窗口)的左右边界,其中左指针代表着上文中「枚举子串的起始位置」,而右指针即为上文中的 rk;
在每一步的操作中,我们会将左指针 i 向右移动一格,表示 我们开始枚举下一个字符作为起始位置,然后我们可以不断地向右移动右指针,但需要保证这两个指针对应的子串中没有重复的字符。在移动结束后,这个子串就对应着 以左指针 i 开始的,不包含重复字符的最长子串。我们记录下这个子串的长度;
在枚举结束后,我们找到的最长的子串的长度即为答案。
来源:力扣(LeetCode)
代码思路:
设置一个无重复的unordered_set容器,用来记录个循环里的最长无重复字符串;
设置一个左指针 i 用来指向每次循环最长字符串的起始位置,每次右移一位;
设置一个右指针 rk 用来指向每次循环最长字符串的结束位置,每次右移一位;
在循环中,每次 ++i 要移除occ中的s[i-1],总是让s[i]处于occ起始位置;
在不越界的前提下,如果occ中没有当前s[i],则插入到occ中,并不断取occ中字符串长度的最大值。
class Solution {
public:
int lengthOfLongestSubstring(string s) {
unordered_set<char> occ;
int n = s.size();
int rk = -1, ans = 0;
for (int i = 0; i < n; ++i) {
if (i != 0) {
occ.erase(s[i - 1]);
}
while (rk + 1 < n && !occ.count(s[rk + 1])) {
occ.insert(s[rk + 1]);
++rk;
}
ans = max(ans, rk - i + 1);
}
return ans;
}
};class Solution {
public:
int lengthOfLongestSubstring(string s) {
unordered_set<char> occ;
int n = s.size();
// 右指针,初始值为 -1,相当于我们在字符串的左边界的左侧,还没有开始移动
int rk = -1, ans = 0;
//rk作为s的下标,ans是统计occ中的元素个数。
// 枚举左指针的位置,初始值隐性地表示为 -1
for (int i = 0; i < n; ++i) {
if (i != 0) {
// 左指针向右移动一格,移除一个字符,因为左指针右移后,起始位置改变,移除occ中的s[i-1]
occ.erase(s[i - 1]);
//擦除occ中的s[i-1],s[i-1]是一个迭代器,通过它来删除occ中的与它相同的元素
//i-1,是因为循环中为++i,先++再使用,第一个元素occ中肯定没有
}
//这一循环的作用是遍历一遍occ中是否有当前比较的s[rk+1],如果没有就插入到occ,有的话就不符合条件,跳出循环,
//到i+1继续进入比较
while (rk + 1 < n && !occ.count(s[rk + 1])) {
//若occ中没有出现s[rk+1],count函数返回0,非0为1,循环继续,当出现有相同的字符,返回非0,循环结束
// 不断地移动右指针
occ.insert(s[rk + 1]);
//将不存在重复的s[rk+1]插入到occ中
++rk;
}
// occ中第 i 到 rk 个字符是一个极长的无重复字符子串
ans = max(ans, rk - i + 1);
//记录最大无重复长度
}
return ans;
}
};4.? 寻找两个正序数组的中位数(hard)
直接CV了。。。。。。。

因为要求了时间复杂度,所以不能简单地将m和n两个数组合并,再排序找中位数。?
二分查找:?
主要思路:要找到第 k (k>1) 小的元素,那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较
? ? ? ? ?* 这里的 "/" 表示整除
? ? ? ? ?* nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个
? ? ? ? ?* nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个
? ? ? ? ?* 取 pivot = min(pivot1, pivot2),两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个
? ? ? ? ?* 这样 pivot 本身最大也只能是第 k-1 小的元素
? ? ? ? ?* 如果 pivot = pivot1,那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums1 数组
? ? ? ? ?* 如果 pivot = pivot2,那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除",剩下的作为新的 nums2 数组
? ? ? ? ?* 由于我们 "删除" 了一些元素(这些元素都比第 k 小的元素要小),因此需要修改 k 的值,减去删除的数的个数
? ? ? ? ?*/
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/median-of-two-sorted-arrays/solution/xun-zhao-liang-ge-you-xu-shu-zu-de-zhong-wei-s-114/
来源:力扣(LeetCode)
class Solution {
public:
int getKthElement(const vector<int>& nums1, const vector<int>& nums2, int k) {
int m = nums1.size();
int n = nums2.size();
int index1 = 0, index2 = 0;
while (true) {
// 边界情况
if (index1 == m) {
return nums2[index2 + k - 1];
}
if (index2 == n) {
return nums1[index1 + k - 1];
}
if (k == 1) {
return min(nums1[index1], nums2[index2]);
}
// 正常情况
int newIndex1 = min(index1 + k / 2 - 1, m - 1);
int newIndex2 = min(index2 + k / 2 - 1, n - 1);
int pivot1 = nums1[newIndex1];
int pivot2 = nums2[newIndex2];
if (pivot1 <= pivot2) {
k -= newIndex1 - index1 + 1;
index1 = newIndex1 + 1;
}
else {
k -= newIndex2 - index2 + 1;
index2 = newIndex2 + 1;
}
}
}
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int totalLength = nums1.size() + nums2.size();
if (totalLength % 2 == 1) {
return getKthElement(nums1, nums2, (totalLength + 1) / 2);
}
else {
return (getKthElement(nums1, nums2, totalLength / 2) + getKthElement(nums1, nums2, totalLength / 2 + 1)) / 2.0;
}
}
};5. 最长回文子串(mid)

动态规划DP思路:?
首先,只含有一个元素的字符串肯定是回文串;
基本思想:采用动态回归,先比较指定长度为L(从2到n)的一个子字符串的 第一个字符 和 最后一个字符 是否相等,如果相等则继续比较第二个字符和倒数第二个字符,如果直到这个字符串的中间位置,以上都成立,则为回文串。这里用dp[i][j] = true表示从 i 到 j 为回文串。
求得在以上过程中所出现的回文串的最大长度。
//方法1
class Solution {
public:
string longestPalindrome(string s) {
int n=s.size();
if(n<2){
return s;
}
int maxLen=1;
int begin=0;
vector<vector<int>> dp(n,vector<int>(n));
for(int i=0;i<n;i++)
{
dp[i][i]=true;
}
for(int L=2;L<=n;L++)
{
for(int i=0;i<n;i++)
{
int j=L+i-1;
if(j>=n)
{
break;
}
if(s[i]!=s[j])
{
dp[i][j]=false;
}
else
{
if(j-i<3){
dp[i][j]=true;
}else{
dp[i][j]=dp[i+1][j-1];
}
}
if(dp[i][j]&&j-i+1>maxLen)
{
maxLen=j-i+1;
begin=i;
}
}
}
return s.substr(begin,maxLen);
}
};class Solution {
public:
string longestPalindrome(string s) {
int n=s.size();//s大小
if(n<2){
return s;//只有一个元素时,肯定为回文串。字符串为空时,返回空
}
int maxLen=1;//最大回文串长度
int begin=0;//回文串开始位置
//dp[i][j]表示s[i...j]是否是回文串
vector<vector<int>> dp(n,vector<int>(n));//n*n个
//vector容器中放的元素类型是vector型,后面的vector容器中放的是int型,相当于二维容器
//初始化
for(int i=0;i<n;i++)
{
dp[i][i]=true;
}
//L是要判断的字符串长度,i和j是要判断字符串的头尾
//递推开始
//先枚举子串长度
for(int L=2;L<=n;L++)//从含2个字符的字符串开始遍历
{
//枚举左边界,左边界的上限设置可以宽松一点
for(int i=0;i<n;i++)//从这L个的字符串的第一个开始遍历,寻找第一个和最后一个,以及其他对称字符的关系
{
int j=L+i-1;//边界为j,字符串长度为L=j-i+1
//i是要判断字符串的左边界,j是要判断字符串的右边界
if(j>=n)//当右边界超过原字符串的长度时,跳出循环,比较结束
{
break;
}
if(s[i]!=s[j])
{//一个字符串的两头元素不同,则从i到j的字符串不为回文串
dp[i][j]=false;
}
else
{//一个字符串的两头元素相同
if(j-i<3){//字符个数小于3的字符串,两头元素相等肯定为回文串
dp[i][j]=true;
}else{
dp[i][j]=dp[i+1][j-1];//两头的元素向中间进一步,判断进一步是不是相同的元素
}
}
if(dp[i][j]&&j-i+1>maxLen)//i到j为true,并且L>maxLen
{
maxLen=j-i+1;//取大值
begin=i;
}
}
}
return s.substr(begin,maxLen);//从begin(i)开始取maxLen个字符返回
}
};从中心往外拓展思路:?
回文串分两种情况,一种是中心只有一个字符bab,另一种时中心两个字符baab;
设置一个函数,从第i个位置作为中心开始,来检验是否s[left]==s[right],当遇到两头不相等的情况时,返回上一个位置;
方法2
class Solution {
public:
//pair将一对值(T1和T2)组合成一个值
//这一对值可以具有不同的数据类型(T1和T2)
//两个值可以分别用pair的两个公有函数first和second访问。
pair<int, int> expandAroundCenter(const string& s, int left, int right) {
while (left >= 0 && right < s.size() && s[left] == s[right]) {
--left;
++right;
}
return {left + 1, right - 1};//返回从中心开始两侧对应位置相同的回文字符串
}
string longestPalindrome(string s) {
int start = 0, end = 0;//start--end之间的字符串为回文串
for (int i = 0; i < s.size(); ++i) {
auto [left1, right1] = expandAroundCenter(s, i, i);//cbabc,一个中心
auto [left2, right2] = expandAroundCenter(s, i, i + 1);//cbaabc,两个中心
//符合哪种情况用哪个
if (right1 - left1 > end - start) {//一个中心
start = left1;
end = right1;
}
if (right2 - left2 > end - start) {//两个中心
start = left2;
end = right2;
}
}
return s.substr(start, end - start + 1);
}
};