链表中环的入口结点

原题链接
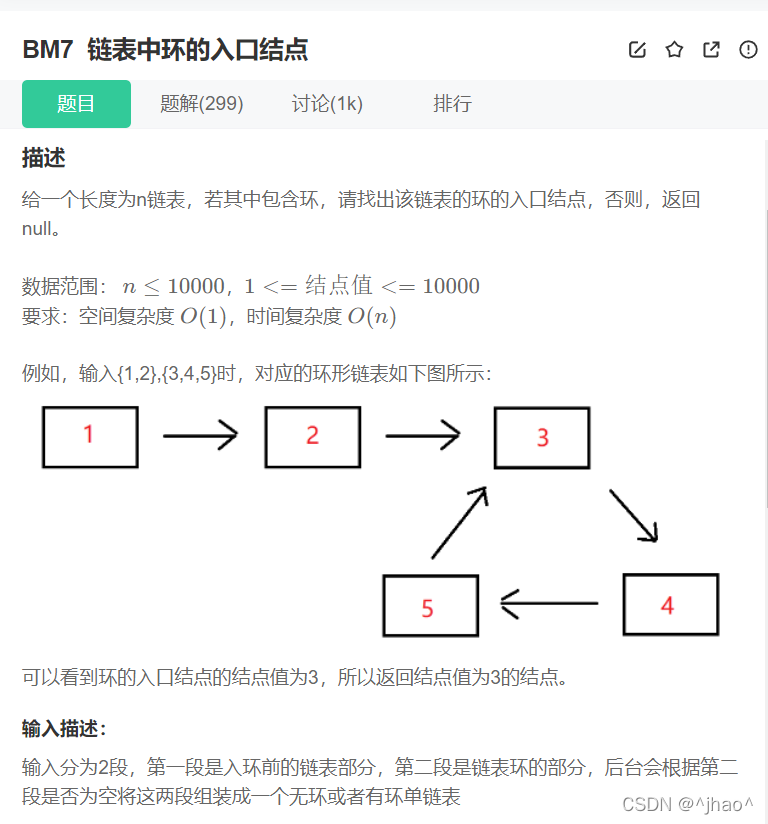
在这里插入图片描述
思路：含有环，找头部，此时我们的思路可以是快慢指针的方式找到同一个位置，此时这个位置是两个链表的公共节点。此时一个链表从头开始走，一个链表从公共节点开始走，就能保证走到该位置。

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) :
        val(x), next(NULL) {
    }
};
*/
class Solution {
public:
    ListNode* EntryNodeOfLoop(ListNode* pHead) {
        if(pHead ==nullptr || pHead->next == nullptr)
            return nullptr;
  
        ListNode* cur = pHead;
        ListNode* nextnext = pHead;
       // ListNode* pre = pHead;
        while(nextnext && nextnext->next)
        {
            //pre = cur;
            cur = cur->next;
            nextnext = nextnext->next;
            nextnext = nextnext->next;
            if(cur == nextnext)
                break;
        }
        //cur为公共的节点
        //断开链接

        //pre->next = nullptr;
        
        //问题转化成如何两个链表找公共节点
        ListNode* pre = pHead;
        //cur ， pre两个节点分别找公共节点
        while(cur && pre)
        {
            if(cur == pre)
                return cur;
            cur = cur->next;
            pre = pre->next;
        }
        return nullptr;
    }
};

为什么这样是对的？

结论一：慢指针进入环内走不到一圈就会被快指针追上。
解释：慢指针走一圈，快指针都能走上两圈了！
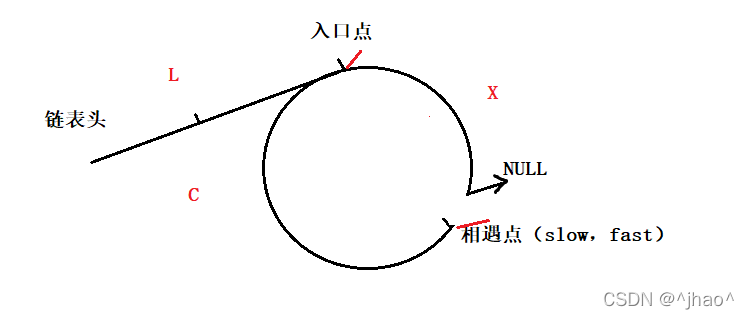
结论二：快指针从相遇点到入口点的距离：
L + N*C + X（N >= 1），L表示头节点到入口点的距离，X表示入口点到相遇点的距离，C表示环的周长。
慢指针到相遇点的距离是 L + X
在这里插入图片描述

fast一次走n步（n>2）行不？

不行。当C是环的周长，N是slow指针刚走进环的时候与快指针之间的差距距离。
倘若快指针一次走三步，那么差距是2步的减少的，那么这个过程倘若N是奇数，那么当快指针追赶慢指针的过程中会越过他一步，此时距离差变成C-1，倘若C-1是奇数，即N=C-1，那么是不是就死循环？

当然只要保持fast走的步数单次比slow多一步即可。

第二种思路

在相遇点，倘若将链表的结构断开，此时从相遇点和链表头同时出发，找到公共节点，这个题实际上就变成了链表中环的入口结点。
在这里插入图片描述

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) :
        val(x), next(NULL) {
    }
};
*/
class Solution {
public:
    ListNode* EntryNodeOfLoop(ListNode* pHead) {
        if(pHead == nullptr || pHead->next == nullptr)
            return nullptr;
        ListNode* cur = pHead;
        ListNode* next = cur;
        ListNode* pre = nullptr;
        while(next && next->next)
        {
            pre = cur;
            cur = cur->next;
            next = next->next;
            next = next->next;
            if(cur == next)
                break;
        }

        pre->next = nullptr;
        ///问题转化为两个指针找交点,cur为相遇点
        ListNode* sub1 = pHead;
        ListNode* sub2 = cur;
        int count1 = 0,count2 = 0;
        while(sub1)
        {
            count1++;
            sub1=sub1->next;
        }
        //判断sub2是否还带环
        ListNode* tmp = sub2;
        ListNode* tmpnext = sub2;
        while(tmpnext && tmpnext->next)
        {
            tmp = tmp->next;
            tmpnext = tmpnext->next;
            tmpnext = tmpnext->next;
            if(tmp == tmpnext)
                return cur;//带环
        }
        while(sub2)
        {
            //若是带环的，这里有一种情况会出错
            count2++;
            sub2=sub2->next;
        }
        int cnt = abs(count2-count1);
        ListNode* sub3 = count1>count2?pHead:cur;
        ListNode* sub4 = sub3==pHead?cur:pHead;
        while(cnt--)
        {
            sub3 = sub3->next;
        }
        while(sub3 && sub4)
        {
            if(sub3 == sub4)
                return sub3;
            sub3 = sub3->next;
            sub4 = sub4->next;
        }
        return nullptr;  
    }
};