
这一篇内容拖了非常长都没有写,现在进行书写!
树
基本概念
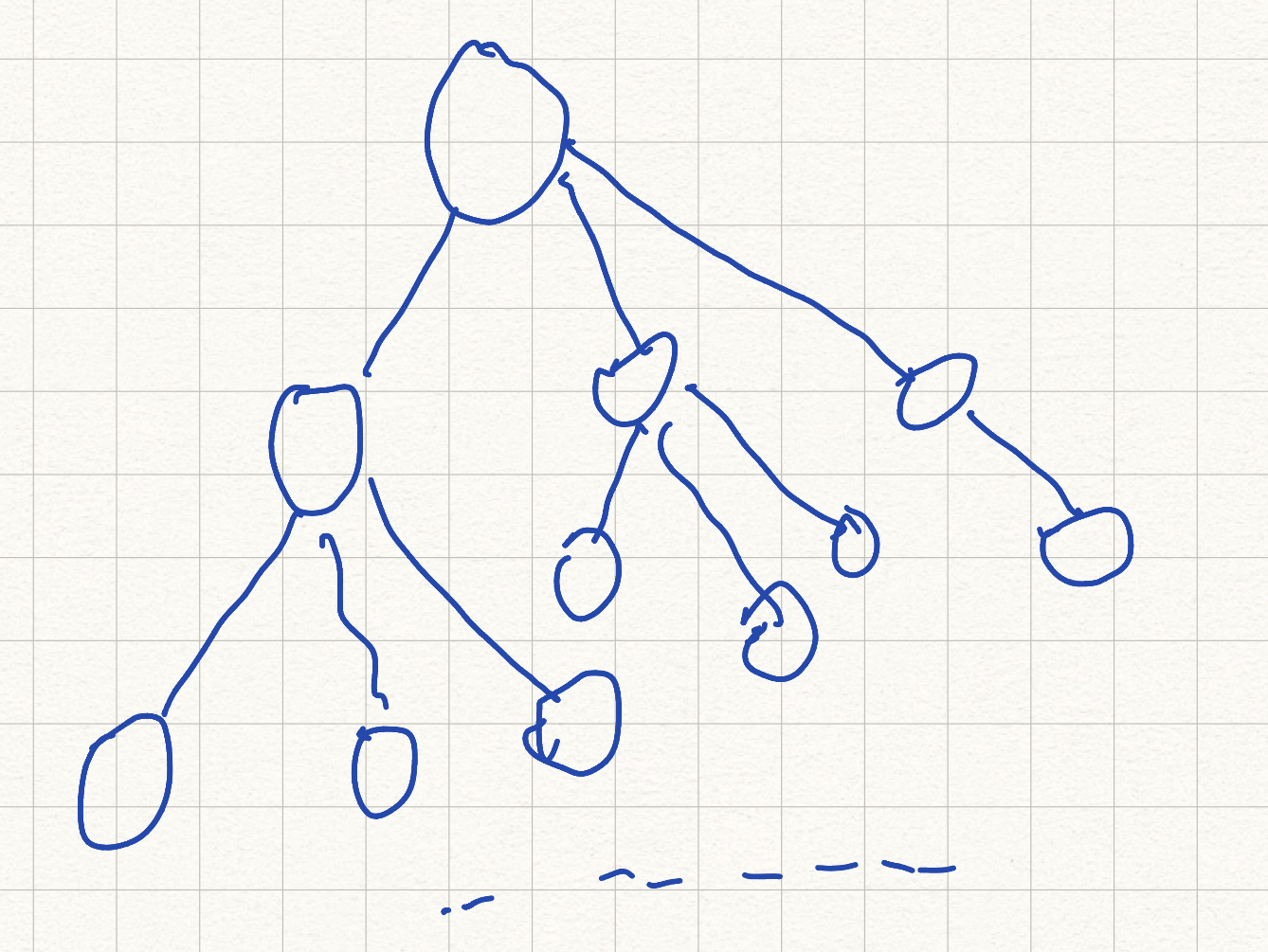
单一的孩子节点之间没有相交。
节点的度:一个节点含有的子树的个数称为该节点的度;
叶节点或终端节点:度为O的节点称为叶节点;
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
兄弟节点:具有相同父节点的节点互称为兄弟节点;
树的度:一棵树中,最大的节点的度称为树的度;
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次
堂兄弟节点:双亲在同一层的节点互为堂兄弟;
节点的祖先:从根到该节点所经分支上的所有告点.
子孙:以某节点为根的子树中任一节点都称为该节点的子孙,如上图:所有节点都是A的子孙
森林:由m (m>0)棵互不相交的树的集合称为森林;
表示方法
孩子兄弟表示法。
typedef int DataType;
struct Node
{
struct Node* firstChildl;
struct Node* pNextBrother;
DataType data;
}
二叉树
基本的概念
特殊的一种树的结构。
1,二叉树不存在度大于2度节点
2,有左右之分
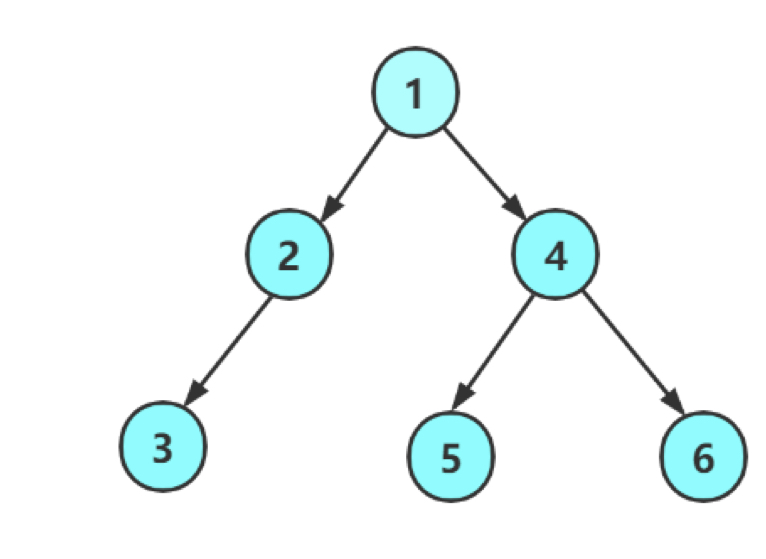
特殊的二叉树
每一层的节点都到达最大值。
二叉树的性质
基本了解可以了!
1. 若规定根节点的层数为1,则一棵非空二叉树的第识上最多有2^(i - 1)个结点。
2.若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h - 1。
3.对任何一棵二叉树,如果度为0其叶结点个数为 N0,度为2的分支结点个数为 N2,则有N0 = N2 +1。
4.若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=lg(n + 1)。
为底,n+1为对数)
2. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号
3. ,则对
千序号为的结点有:
4. 若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
2.若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
5. 若2it2<n,右孩子序号:2it2,2i+2>=n否则无右孩子
二叉树储存结构
顺序储存
利用数组进行储存,只适合完全二叉树。数据储存是数组,逻辑上面是二叉树。
链式结构
暂时不讨论这个!
堆
一个集合完全按照二叉树的方式进行储存,满足子子节点全部大于或者小于父节点,成为大堆或者小堆。
数组建立堆
向下调整建堆,插入数据建立堆
数据不断的增多,是从上到下增多的。时间复杂的为O(N)
void AdjustUp(HeapData *pa,size_t child){
size_t parent = (child -1)/2;
while (parent > 0) {
if (pa[parent]<pa[child]) {
int tmp = pa[child];
pa[child] = pa[parent];
pa[parent] = tmp;
child = parent;
parent = (child - 1)/2;
}
else
break;
}
}
for(int n = 0;n < size;n++){
AdjustUp(a,n);
}
向上调整建堆
从下面的子树进行调整(非叶子节点开始),整个过程都是从父亲节点开始减!
时间复杂度为O(NlgN)

for(int n = (size - 1 - 1)/2;n >= 0 ;i--){//从第一个父亲节点进行调整。
//第一个子节点为size - 1,利用公式解决问题
AdjustDown(a,size,n);
}
一个元素从最底层到最高层满足相应的条件。
堆排序
基本概念:利用堆特性进行排序。(然后可以得到一个完整堆安装大小排列数组)!
首先建立堆
升序建大堆,降序建立小堆。
如果升序建立小堆,交换之后堆顺序完全改变了,只有重新建堆了,还不如直接选择最大那一个,
还不用怎么复杂。
建立大堆,只用向下面调整可以了!
升序排序:
选择一个最大堆,然后让最大堆内容节点与最小的哪一个节点交换。然后继续进行堆排序(堆的数量减小1),一直重复上面操作,直到只有一个节点。
