DSA数字签名算法基于SHA1哈希算法,关于SHA1的实现看另一篇文章。
一、什么是DSA
数字签名标准(DSS)由NIST公布,该标准能够使接收者能够验证数据的完整性和数据发送者的身份而制定,所采用的算法称为DSA算法,也称为DSA签名。
二、DSA签名算法流程
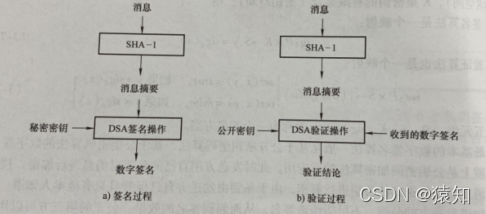
DSA签名涉及四个参数,p,q,g,y和x,中前四者构成公钥,x为私钥(x<q)。
依据DSS标准,p为512~1024位,q是160位长的素数,且q|p-1;g=h(p-1)/q mod p,其中h是一整数,1<h<(p-1)且(h(p-1)/q mod p)>1;H(m)为参与签名的杂凑值,DSS选用SHA杂凑算法
(1)DSA 签名过程:
用户随机选取k要求0<k<q,计算:

(2)DSA验证过程:
接收者收到M,r,s后,首先验证0<r<q, 0<s<q,如果通过则计算:

如果v=r,则确认签名正确
三、具体实现过程(附代码)
我们实验要求参数可以设置成较小的,方便计算,如果大家严格按照算法参数要求设置需要改动。
(1)参数设置
算法的一些参数可以看要求设置成随机数,符合大小要求即可,我这里直接使用固定值先进行计算。
参数:
P、Q、H:人员输入,P要求是素数,512-1024位且位数L为64的倍数,Q为p-1的素因数比特长度160位,H是一个整数且1<H<p-1,并且要求g=h^(p-1)/q modp>1
X:(私钥)随机或伪随机整数,0<x<q,我这里设置成了75
K:随机数,0<k<q,我这里设置成了50
pqh = input("请输入P,Q,H的值:\n").split()
p, q, h = int(pqh[0]), int(pqh[1]), int(pqh[2])
g = int((h**(int((p-1)/q))) % p)
k = 50
x = 75
y = int(g**x % p)
print(f"P:{p},Q:{q},G:{g},x:{x},y:{y}")
(2)乘法逆元
乘法逆元:若存在正整数a,b,p, 满足ab = 1(mod p), 则称a 是b 的乘法逆元, 或称b 是a 的乘法逆元。

def EX_GCD(a, b, arr): # 扩展欧几里得
if b == 0:
arr[0] = 1
arr[1] = 0
return a
g = EX_GCD(b, a % b, arr)
t = arr[0]
arr[0] = arr[1]
arr[1] = t - int(a / b) * arr[1]
return g
def ModReverse(a, n): # ax=1(mod n) 求a模n的乘法逆x
arr = [0, 1, ]
gcd = EX_GCD(a, n, arr)
if gcd == 1:
return (arr[0] % n + n) % n
else:
return -1
(3)签名
def sign(g, p, q, x, M):
r = int((g**k % p) % q)
s = int((ModReverse(k, q)*(M+x*r)) % q)
print(f"签名为({r}, {s})")
return r, s
(4)验证
def verify(g, p, q, y, M, r, s):
w = int(ModReverse(s, q) % q)
u1 = int((M*w) % q)
u2 = int(r*w % q)
v = int(((g**u1)*(y**u2) % p) % q)
print(f"lc(w,u1,u2,v)=({w},{u1},{u2},{v})")
if v == r:
print("签名有效")
else:
print("签名无效")
四、跟着demo去debug
这里使用给出两组数据供大家调试,一组来源于课本,一组来源于网络。
(1)示例1:


(2)示例2:

五、完整代码
本次实验课作业上交后补充
