哈喽!这里是一只派大鑫,不是派大星。本着基础不牢,地动山摇的学习态度,从基础的C语言语法讲到算法再到更高级的语法及框架的学习。更好地让同样热爱编程(或是应付期末考试 狗头.jpg)的大家能够在学习阶段找到好的方法、路线,让天下没有难学的程序(只有秃头的程序员 2333),学会程序和算法,走遍天下都不怕!
目录
引言
本文从最基础的什么栈、队列是开始,依次讲解顺序栈、共享栈、链栈、顺序队列、循环队列、链队列,并给出参考代码,相信哪怕是小白的你,在看完文章后也能豁然开朗。
妈妈再也不担心我不会手写数据结构了

一、什么是栈
栈 在百度百科中是这样定义的:
栈作为一种数据结构,是一种只能在一端进行插入和删除操作的特殊线性表。
它按照后进先出的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶,需要读数据的时候从栈顶开始弹出数据(最后一个数据被第一个读出来)。
栈顶、栈底:允许进行插入和删除操作的一端称为栈顶(top),另一端为栈底(bottom)。栈底固定,而栈顶浮动。
空栈:栈中元素个数为零时称为空栈。
进栈:插入一般称为进栈(PUSH)。
出栈:删除则称为退栈(POP)。

?
1.1顺序栈
1.1.1顺序栈的存储结构
顺序栈,即用顺序表实现栈存储结构。
通过前面的学习我们知道,使用栈存储结构操作数据元素必须遵守 "先进后出" 的原则,
如果你仔细观察顺序表(底层实现是数组)和栈结构就会发现,它们存储数据的方式高度相似,只不过栈对数据的存取过程有特殊的限制,而顺序表没有。
例如,我们先使用顺序栈(a 数组)存储?{1,2,3,4},存储状态如下图所示:
?
?于是我们可以很清楚的得到,顺序栈的存储结构就是这样的:
const int MAXSIZE = 10; //顺序栈的存储结构 typedef struct{ int data[MAXSIZE]; int top = -1; //top指向栈顶 }SqStack;
栈空
很自然的,我们将top初始化为-1,代表栈空的状态?top == -1
//判断栈是否为空 int IsEmpty(SqStack s){ if(s.top == -1) return 1;//空 return 0; }

?
栈满
因为MaxSize代表的是最大存储个数,所以我们top最大的下标只能到MaxSize-1,
所以当 top == MaxSize - 1 时即为栈满的状态

?
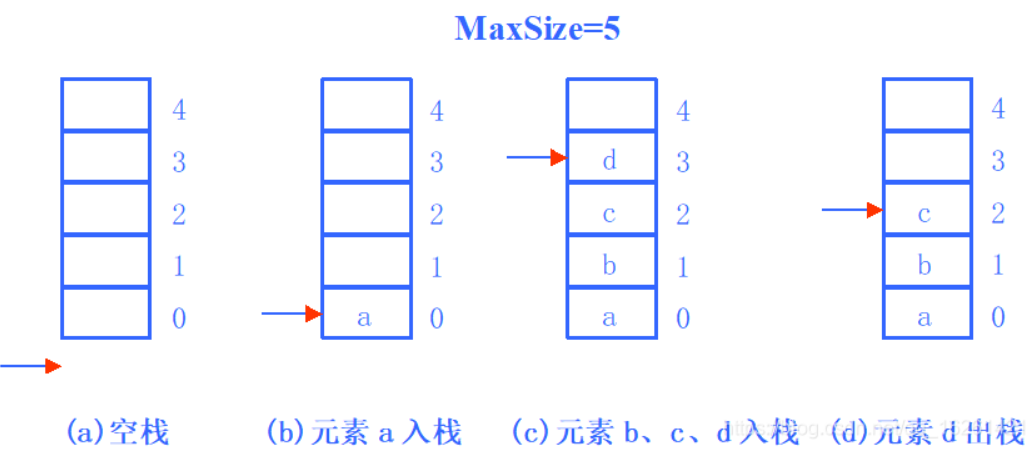
下面我们将数组“竖着”放置来看,进行出栈、入栈的学习~~~
?
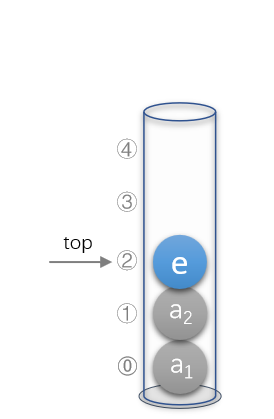
1.1.2入栈
首先我们需要明确,因为栈限制在一端进行数据的输入输出,所以我们只需要对top进行移动即可实现。
对于入栈(栈不满的情况下),设想一下,我们应该先找到“空出位置的编号”,再将其“对号入座”,而top是栈顶元素的下标,所以我们要先将top++,再将数组对应top位置赋值。
//进栈
void Push(SqStack *s,int e){
if(s->top == MAXSIZE - 1){ // 栈满的情况
printf("栈满~\n");
return;
}
s->data[++s->top] = e; //按照优先级,先取s->top 然后自增1
} ?
? ?
?
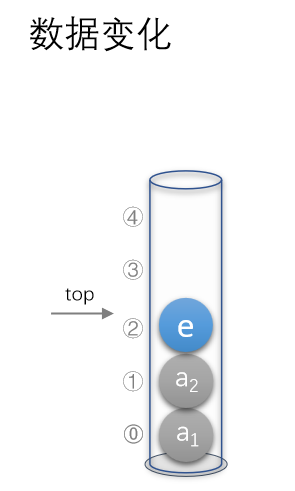
1.1.3出栈
同样的,出栈我们应该先得到栈顶元素的数据,然后在将其栈顶位置下标减1即可
(实际上原来top下标的数据仍然存在于数组中,但是并不在栈中,因为它不在top范围内)?
//出栈
int Pop(SqStack *s){
if(s->top == -1){ // 栈空的情况
printf("栈空~\n");
return -1;
}
return s->data[s->top--];
} ?
? ?
?
1.1.4顺序栈完整代码
#include<stdio.h>
#include<iostream>
#include<math.h>
using namespace std;
//顺序栈的实现
const int MAXSIZE = 10;
//顺序栈的存储结构
typedef struct{
int data[MAXSIZE];
int top = -1; //top指向栈顶
}SqStack;
//判断栈是否为空
int IsEmpty(SqStack s){
if(s.top == -1) return 1;//空
return 0;
}
//进栈
void Push(SqStack *s,int e){
if(s->top == MAXSIZE - 1){ // 栈满的情况
printf("栈满~\n");
return;
}
s->data[++s->top] = e;
}
//出栈
int Pop(SqStack *s){
if(s->top == -1){ // 栈空的情况
printf("栈空~\n");
return -1;
}
return s->data[s->top--];
}
//打印
void Print(SqStack s){
while(! IsEmpty(s)){
printf("%d ",Pop(&s));
}
// for(int i = 0; i <= s.top; i++){ //方式二
// printf("%d ",s.data[i]);
// }
printf("\n");
}
int main(){
SqStack s;
Push(&s,3);
Push(&s,6);
Push(&s,9);
Print(s);
return 0;
}1.2共享栈
对于一个栈,我们也只能尽量考虑周全,设计出合适大小的数组来处理,但对于两个相同类型的栈,我们却可以做到最大限度地利用其实现开辟的存储空间来进行操作。
如果我们有两个相同类型的栈,我们为它们各自开辟了数组空间,极有可能是第一个栈满了,再进栈就溢出了,而另一个栈还有很多存储空间空闲,这又何必呢?
我们完全可以用一个数组来存储两个栈,充分利用这个数组占用的内存空间,只不过需要点小技巧~~~
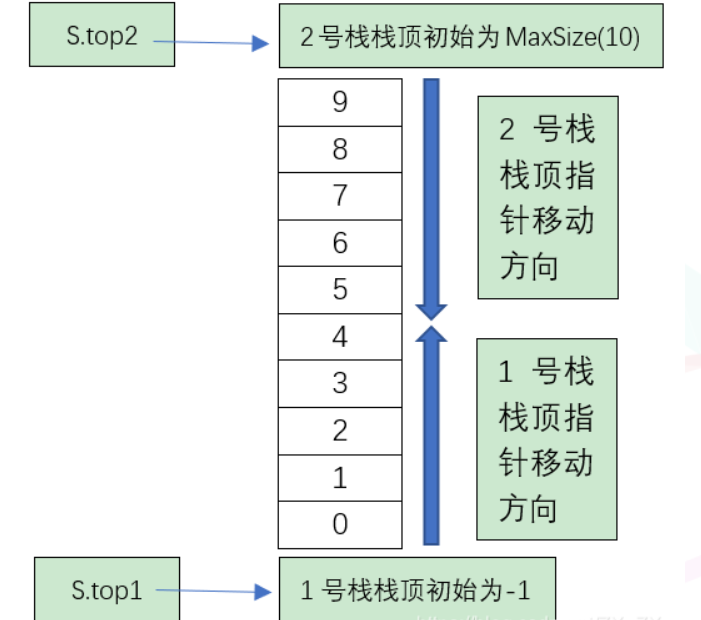
我们的做法如下图,数组有两个端点,两个栈有两个栈底,
让一个栈的栈顶为-1,另一个栈的栈顶为MaxSize
这样如果两个栈增加元素,就是两栈顶向中间靠拢
?

?
1.2.1共享栈的存储结构
利用栈底位置不变的特性,可让两个顺序栈共享一个一维数组空间,将两个栈的栈底分别设置在共享空间的两端,两个栈顶向共享空间的中间延伸。共享栈是为了更有效地利用存储空间,两个栈的空间相互调节,只有在整个存储空间被占满时才发生上溢。
所以我们可以得到共享栈的存储结构:
const int MAXSIZE = 10; //共享栈的存储结构 typedef struct{ int data[MAXSIZE]; int top1 = -1; int top2 = MAXSIZE; // 初始栈空状态 }DStack;
栈空
对于top1的栈,就是上文顺序栈一样,top1 == -1即为栈空
对于top2的栈,当top2 == MaxSize 时即为栈空
//判断空
int IsEmpty(DStack s,int num){ //判断编号1、2栈的情况
if(num == 1) return s.top1 == -1;
else return s.top2 == MAXSIZE;
}栈满
由于两个栈是向中间“靠拢”一样,所以当top1 + 1 == top2 时即为栈满状态,如下图所示:

1.2.2入栈
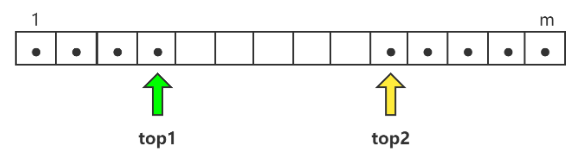
对于1号栈,先++top1然后将top位置赋值
对于2号栈,先--top2然后将top位置赋值(因为入栈是“靠拢”的过程)
//进栈
void Push(DStack *s,int e,int num){
if(s->top1 + 1 == s->top2){
printf("栈满~\n");
return;
}
if(num == 1){
s->data[++s->top1] = e;
}else{
s->data[--s->top2] = e;
}
}1.2.3出栈
对于1号栈,先得到top1位置的值,再将top1减一
对于2号栈,先得到top2位置的值,再将top1加一(因为出栈是“分离”的过程)
//出栈
int Pop(DStack *s,int num){
if(num == 1){
if(s->top1 == -1){
printf("栈空~\n");
return -1;
}else{
return s->data[s->top1--];
}
}else{
if(s->top2 == MAXSIZE){
printf("栈空~\n");
return -1;
}else{
return s->data[s->top2++];
}
}
}同时,通过对比入栈、出栈,我们可以看出,无论是一个栈,还是两个栈,
入栈都是先移动top再将位置赋值,出栈都是先取出该值再移动top(很重要,需要理解~~)?
所以入栈是 前++(--),出栈是 后--(++)
1.2.4共享栈完整代码
#include<stdio.h>
#include<iostream>
#include<math.h>
using namespace std;
//共享栈的实现
const int MAXSIZE = 10;
//共享栈的存储结构
typedef struct{
int data[MAXSIZE];
int top1 = -1;
int top2 = MAXSIZE; // 初始栈空状态
}DStack;
//判断空
int IsEmpty(DStack s,int num){ //判断编号1、2栈的情况
if(num == 1) return s.top1 == -1;
else return s.top2 == MAXSIZE;
}
//进栈
void Push(DStack *s,int e,int num){
if(s->top1 + 1 == s->top2){
printf("栈满~\n");
return;
}
if(num == 1){
s->data[++s->top1] = e;
}else{
s->data[--s->top2] = e;
}
}
//出栈
int Pop(DStack *s,int num){
if(num == 1){
if(s->top1 == -1){
printf("栈空~\n");
return -1;
}else{
return s->data[s->top1--];
}
}else{
if(s->top2 == MAXSIZE){
printf("栈空~\n");
return -1;
}else{
return s->data[s->top2++];
}
}
}
void Print(DStack s,int num){
if(num == 1){
while(s.top1 > -1){
printf("%d ",s.data[s.top1--]);
}
}else{
while(s.top2 < MAXSIZE){
printf("%d ",s.data[s.top2++]);
}
}
printf("\n");
}
int main(){
DStack s;
Push(&s,1,1);
Push(&s,3,1);
Push(&s,5,1);
Push(&s,2,2);
Push(&s,4,2);
Push(&s,6,2);
Print(s,1);
Print(s,2);
Pop(&s,1);
Pop(&s,2);
Print(s,1);
Print(s,2);
return 0;
}1.3链栈
栈的链式存储结构,简称为链栈,就和链表一样,用指针实现的就是单链表
想想看,栈知识栈顶来做插入和删除操作,栈顶放在链表的头部还是尾部呢?
由于单链表有头指针,而栈顶指针也是必需的,那直接让它俩合二为一不就好了!
所以比较好的方法是把栈顶放在单链表的头部。
另外,都已经有了栈顶在头部了,单链表中比较常用的头结点也就失去了意义,通常对于链栈来说,是不需要头结点的。
1.3.1链栈的存储结构
Node结构体和单链表的一样,用于存储数据和下一个指针
LinkStack相当于定义了一个“栈”结构体,里面记录cnt(结点数量),以及栈顶top指针
链栈的操作绝大部分都和单链表类似,只是在插入和删除上特殊一些。
?注意:在链栈中注意指针的方向是从栈顶指向栈底
//链栈的存储结构
typedef struct Node{ //结点的数据
int data;
struct Node *next;
}Node;
typedef struct{ //栈的数据
int cnt;
Node* top;
}LinkStack;栈空
因为top指针即为指向栈顶的指针,如果top == NULL则代表栈空
栈满
对于链栈来说,基本不存在栈满的情况,除非内存已经没有可以使用的空间,
如果真的发生,那此时的计算机操作系统已经面临死机崩溃的情况, 而不是这个链表是否溢出问题。
?初始化
这里采用 LinkStack 非指针的方式定义栈 s,将其初始化后返回给main中定义的s即可
而在调用基本操作的函数时,因为我们只需要修改s里面的top指针,所以函数形参使用指针类型(地址),函数实参 &s 传入地址
(当然也可以像链表一样直接定义为 LinkStack * 类型,实参传入 s即可,效果是一样的)
//初始化栈
LinkStack Init(){
LinkStack s;
s.cnt = 0;
s.top = (Node *)malloc(sizeof(Node));
s.top = NULL;
return s;
}1.3.2入栈
将链表头部作为栈顶的一端,可以避免在实现数据 "入栈" 和 "出栈" 操作时做大量遍历链表的耗时操作。
链表的头部作为栈顶,意味着:
- 在实现数据"入栈"操作时,需要将数据从链表的头部插入;
- 在实现数据"出栈"操作时,需要删除链表头部的首元节点;
链栈实际上就是一个只能采用头插法插入或删除数据的链表
?入栈时类似头插法,用一个指针指向top,然后将top指针的指向和该指针指向一样
//进栈
void Push(LinkStack *s,int e){
Node *p = (Node*)malloc(sizeof(Node));
p->data = e;
p->next = s->top;
s->top = p;
s->cnt++;
}1.3.3出栈
出栈时用p指针指向栈顶(方便free栈顶元素),然后把栈顶的指向 指向下一个结点即可
//出栈
void Pop(LinkStack *s){
if(s->top == NULL){
printf("栈空~\n");
return;
}
Node *p;
printf("%d ",s->top->data);
p = s->top;
s->top = s->top->next;
free(p);
s->cnt--;
}PS:入栈、出栈别忘记更新cnt的值~~~?
1.3.4链栈完整代码
#include<stdio.h>
#include<iostream>
#include<math.h>
using namespace std;
//链栈的实现
//链栈的存储结构
typedef struct Node{ //结点的数据
int data;
struct Node *next;
}Node;
typedef struct{ //栈的数据
int cnt;
Node* top;
}LinkStack;
//初始化栈
LinkStack Init(){
LinkStack s;
s.cnt = 0;
s.top = (Node *)malloc(sizeof(Node));
s.top = NULL;
return s;
}
//判断空
int IsEmpty(LinkStack s){
return s.cnt == 0;
}
//进栈
void Push(LinkStack *s,int e){
Node *p = (Node*)malloc(sizeof(Node));
p->data = e;
p->next = s->top;
s->top = p;
s->cnt++;
}
//出栈
void Pop(LinkStack *s){
if(s->top == NULL){
printf("栈空~\n");
return;
}
Node *p;
printf("%d ",s->top->data);
p = s->top;
s->top = s->top->next;
free(p);
s->cnt--;
}
int main(){
LinkStack s = Init();
Push(&s,1);
Push(&s,3);
Push(&s,5);
Pop(&s);
Pop(&s);
Pop(&s);
Pop(&s);
return 0;
}二、什么是队列
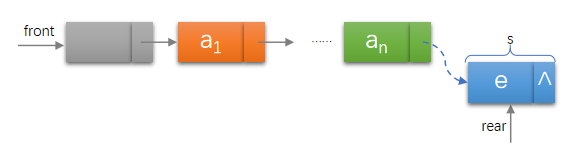
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。
2.1顺序队列
2.1.1顺序队列的存储结构
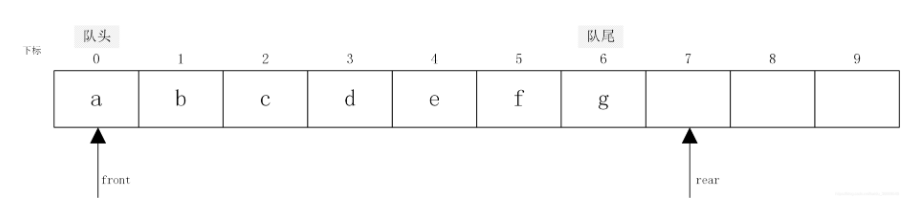
顺序队列通常采用一维数组存储队列中的元素,另外增加两个指针分别指示数组中存放的队首元素和队尾元素。其中指向队首元素的指针称为队头指针front,指向队尾元素下一个位置的指针称为队尾指针rear。
初始化时,队头指针front和队尾指针rear都指向下标为0的存储单元
const int MAXSIZE = 10;
//顺序队列的存储结构
typedef struct Queue{
int data[MAXSIZE];
int front,rear;
}Queue;初始化
初始化就是将front rear的值初始化为0
//初始化
void Init(Queue *q){
q->front = q->rear = 0;
}队列空
当front == rear 的时候就代表队列为空
//判断空
int IsEmpty(Queue q){
if(q.front == q.rear) return 1;
return 0;
}2.1.2入队
?因为rear是最后一个元素的下一个位置下标,所以我们直接将元素存到rear下标处即可
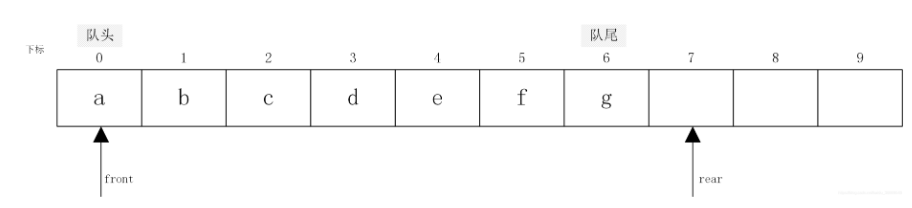
//入队
void Push(Queue *q, int e){
if(q->rear + 1 <= MAXSIZE){
q->data[q->rear++] = e;
}
}2.1.3出队
入队更改rear,出队则更改front
//出队
int Pop(Queue* q){
return q->data[q->front++];
}2.1.4打印队列
很简单,就是从front遍历到rear
//打印队列
void Print(Queue q){
for(int i = q.front ; i < q.rear ; i++)
printf("%d ",q.data[i]);
printf("\n");
}假溢出
但是按照前面介绍的顺序存储方式,容易出现“假溢出”。
所谓“假溢出”,就是经过多次插入和删除操作后,实际队列还有存储空间,但是又无法向队列中插入元素。简单来说就是数组下标越界的错误~~~
例如在图中队列删除a和b,然后依次插入h、i和j,当插入j后,就会出现队尾指针rear越出数组的下界造成“假溢出”,如图
2.1.5顺序队列完整代码
#include<stdio.h>
#include<iostream>
#include<math.h>
using namespace std;
//顺序队列的实现
const int MAXSIZE = 10;
//顺序队列的存储结构
typedef struct Queue{
int data[MAXSIZE];
int front,rear;
}Queue;
//初始化
void Init(Queue *q){
q->front = q->rear = 0;
}
//判断空
int IsEmpty(Queue q){
if(q.front == q.rear) return 1;
return 0;
}
//入队
void Push(Queue *q, int e){
if(q->rear + 1 <= MAXSIZE){
q->data[q->rear++] = e;
}
}
//出队
int Pop(Queue* q){
return q->data[q->front++];
}
//打印队列
void Print(Queue q){
for(int i = q.front ; i < q.rear ; i++)
printf("%d ",q.data[i]);
printf("\n");
}
int main(){
Queue q;
Init(&q);
Push(&q,1);
Push(&q,2);
Push(&q,3);
Push(&q,4);
Print(q);
Pop(&q);
Pop(&q);
Print(q);
return 0;
}2.2循环队列
解决假溢出的办法就是后面满了,再从头开始,也就是“头尾相接”的循环结构
我们把队列的这种头尾相接的顺序存储结构成为循环队列。
当队尾指针rear或队头指针front到达存储空间的最大值时(假定队列的存储空间为QueueSize),让队尾指针或者队头指针转化为0,这样就可以将元素插入到队列的空闲存储单元中,有效的利用存储空间,消除“假溢出”。
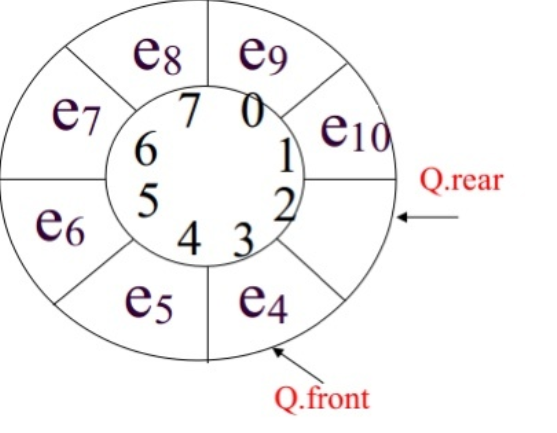
2.2.1循环队列的存储结构
其实循环队列也是用数组存储,只不过为了形象表现出来,我们将图做成一个“环”状,实际上还是线性的数组结构
const int MAXSIZE = 5;
//顺序队列的存储结构
typedef struct Queue{
int data[MAXSIZE];
int front,rear;
}Queue;初始化
初始化将其头尾指针都赋值为0
//初始化
void Init(Queue *q){
q->front = q->rear = 0;
}队列空
显然,当front == rear 表示没有元素,此时队空?
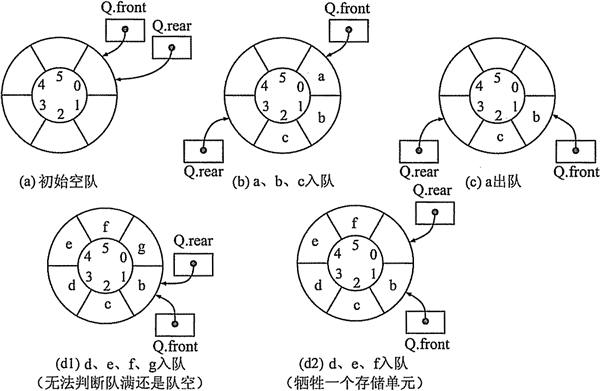
//判断空
int IsEmpty(Queue q){
return q.front == q.rear;
}队列满
那队列满呢?为了和队列空区分
我们不妨让队列多添加一个位置,这个位置不放任何元素,仅仅是为了区别空与满:
由于rear可能比front大或者小,所以它们相差一个位置的时候就是队满,
但也可能相差整整一圈
所以如果最大尺寸为MAXSIZE,
那么当 (rear + 1) % MAXSIZE == front 时就代表队列满了!
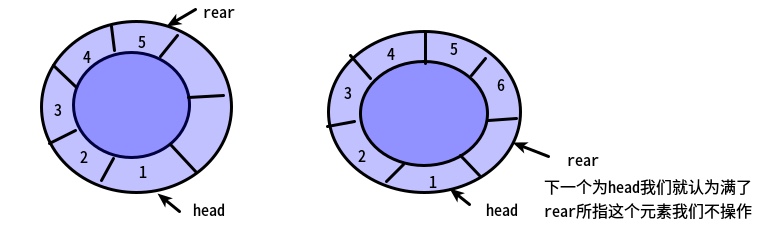
//队列满
int IsFull(Queue q){
return (q.rear+1) % MAXSIZE == q.front;
}获取队列长度
统一rear>front 和 rear<front后的情况,
通用的计算队列长度的公式为:
(rear - front + MAXSIZE) % MAXSIZE
//获取队列长度
int Length(Queue q){
return (q.rear - q.front + MAXSIZE) % MAXSIZE;
}2.2.2入队
很简单,因为rear指向末尾元素的下一个位置,
所以先将元素存储到rear下标处,再将rear下标往“后”移动一个位置即可
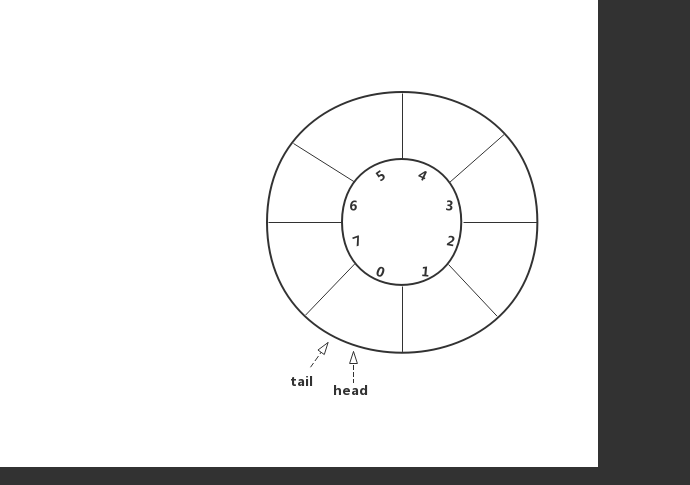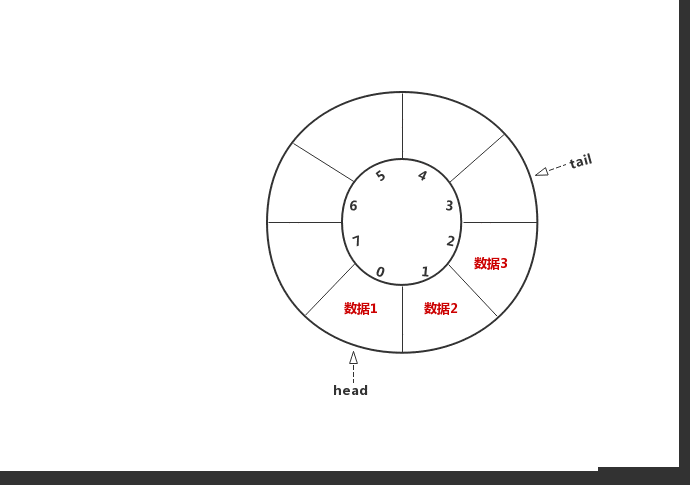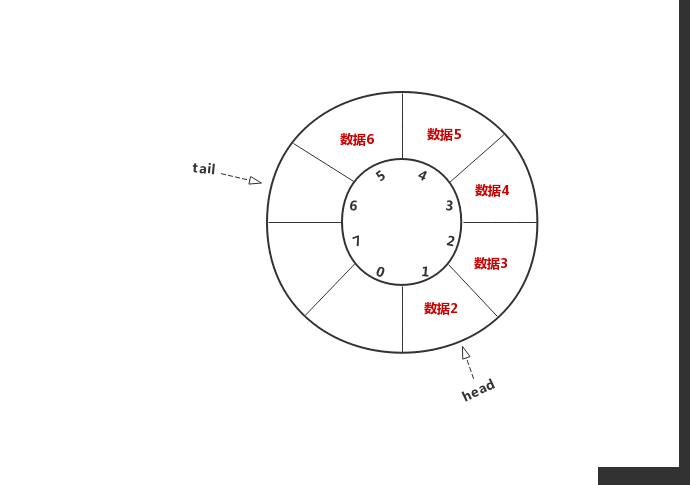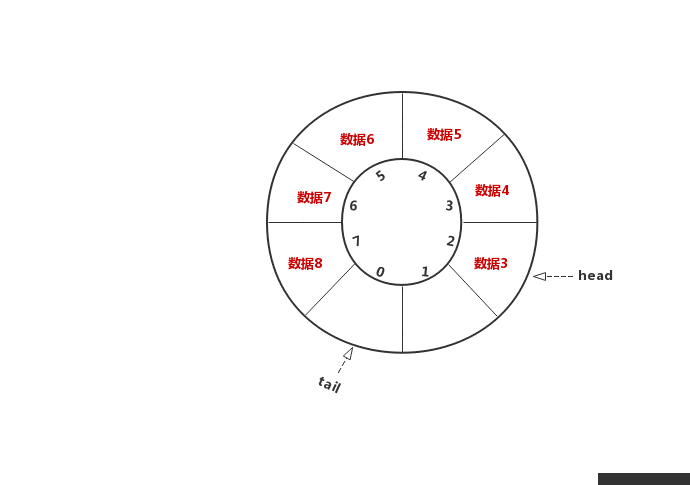
//入队
void Push(Queue *q,int e){
if(IsFull(*q)){
printf("队列满 入队失败~\n");
return;
}
q->data[q->rear] = e;
q->rear = (q->rear + 1) % MAXSIZE;
}2.2.3出队
出队则是更改front指针
//出队
void Pop(Queue *q){
if(IsEmpty(*q)){
printf("队列空 出队失败~\n");
return;
}
printf("%d出队\n",q->data[q->front]);
q->front = (q->front + 1) % MAXSIZE;
}2.2.4打印队列
只要队列不为空,就一直“出队”,这里只是假出队,因为我们传递的是q 根据值传递,只是一个“复制品” 所以并不会真的修改队列q的指针值
//打印
void Print(Queue q){
printf("打印队列元素:\n");
while(! IsEmpty(q)){
printf("%d ",q.data[q.front]);
q.front = (q.front + 1) % MAXSIZE;
}
printf("\n");
}2.2.5循环队列完整代码
#include<stdio.h>
#include<iostream>
#include<math.h>
using namespace std;
//循环队列的实现
const int MAXSIZE = 5;
//顺序队列的存储结构
typedef struct Queue{
int data[MAXSIZE];
int front,rear;
}Queue;
//初始化
void Init(Queue *q){
q->front = q->rear = 0;
}
//判断空
int IsEmpty(Queue q){
return q.front == q.rear;
}
//队列满
int IsFull(Queue q){
return (q.rear+1) % MAXSIZE == q.front;
}
//获取队列长度
int Length(Queue q){
return (q.rear - q.front + MAXSIZE) % MAXSIZE;
}
//入队
void Push(Queue *q,int e){
if(IsFull(*q)){
printf("队列满 入队失败~\n");
return;
}
q->data[q->rear] = e;
q->rear = (q->rear + 1) % MAXSIZE;
}
//出队
void Pop(Queue *q){
if(IsEmpty(*q)){
printf("队列空 出队失败~\n");
return;
}
printf("%d出队\n",q->data[q->front]);
q->front = (q->front + 1) % MAXSIZE;
}
//打印
void Print(Queue q){
printf("打印队列元素:\n");
while(! IsEmpty(q)){
printf("%d ",q.data[q.front]);
q.front = (q.front + 1) % MAXSIZE;
}
printf("\n");
}
int main(){
Queue q;
Init(&q);
printf("队列长度为:%d\n",Length(q));
Pop(&q);
Push(&q,1);
Push(&q,2);
Push(&q,3);
Push(&q,4);
Push(&q,5);
printf("指针值:%d %d\n",q.front,q.rear);
Pop(&q);
Pop(&q);
printf("打印前指针值:%d %d\n",q.front,q.rear);
Print(q);
printf("打印后指针值:%d %d\n",q.front,q.rear);
return 0;
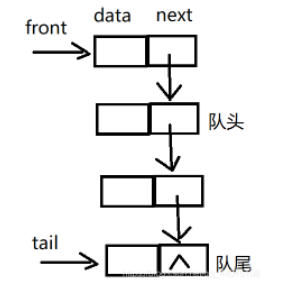
}2.3链队列
队列的链式存储结构,其实就是线性表的单链表,只不过它只能尾进头出而已,
我们把它简称为链队列。
为了操作上的方便,我们将对头指针指向链队列的头结点,而队尾指针指向终端节点
2.3.1链队列的存储结构
将整个结构分为结点的存储和队列的存储,
结点存储data数据和next指针
队列存储头结点和尾指针以及队列长度
//结点的存储结构
typedef struct Node{
int data;
struct Node *Next;
}Node;
//链队列的存储结构
typedef struct Queue{
Node *front,*rear;
int length;
}Queue;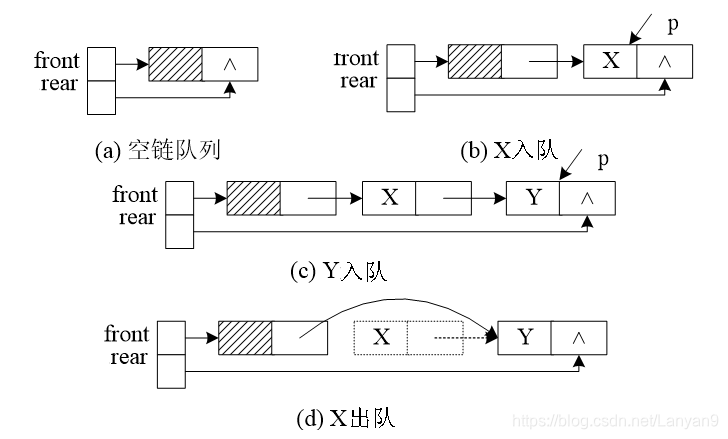
初始化
将队列的front、rear指针指向同一块地址区域作为头结点,不存储值
//初始化
void Init(Queue *q){
q->front = (Node *)malloc(sizeof(Node));
q->rear = q->front;
q->length = 0;
}队列空
判断队列空有两种方法,一种是直接由长度得出,另一种是判断rear和front指针是否重合
//判断空
int IsEmpty(Queue q){
if(q.length == 0)return 1;
return 0;
}队列满
链队列不考虑队列满的情况
获取长度
直接返回队列的length属性即可
//获取长度
void Length(Queue q){
printf("当前队列长度为:%d\n",q.length);
}2.3.2入队
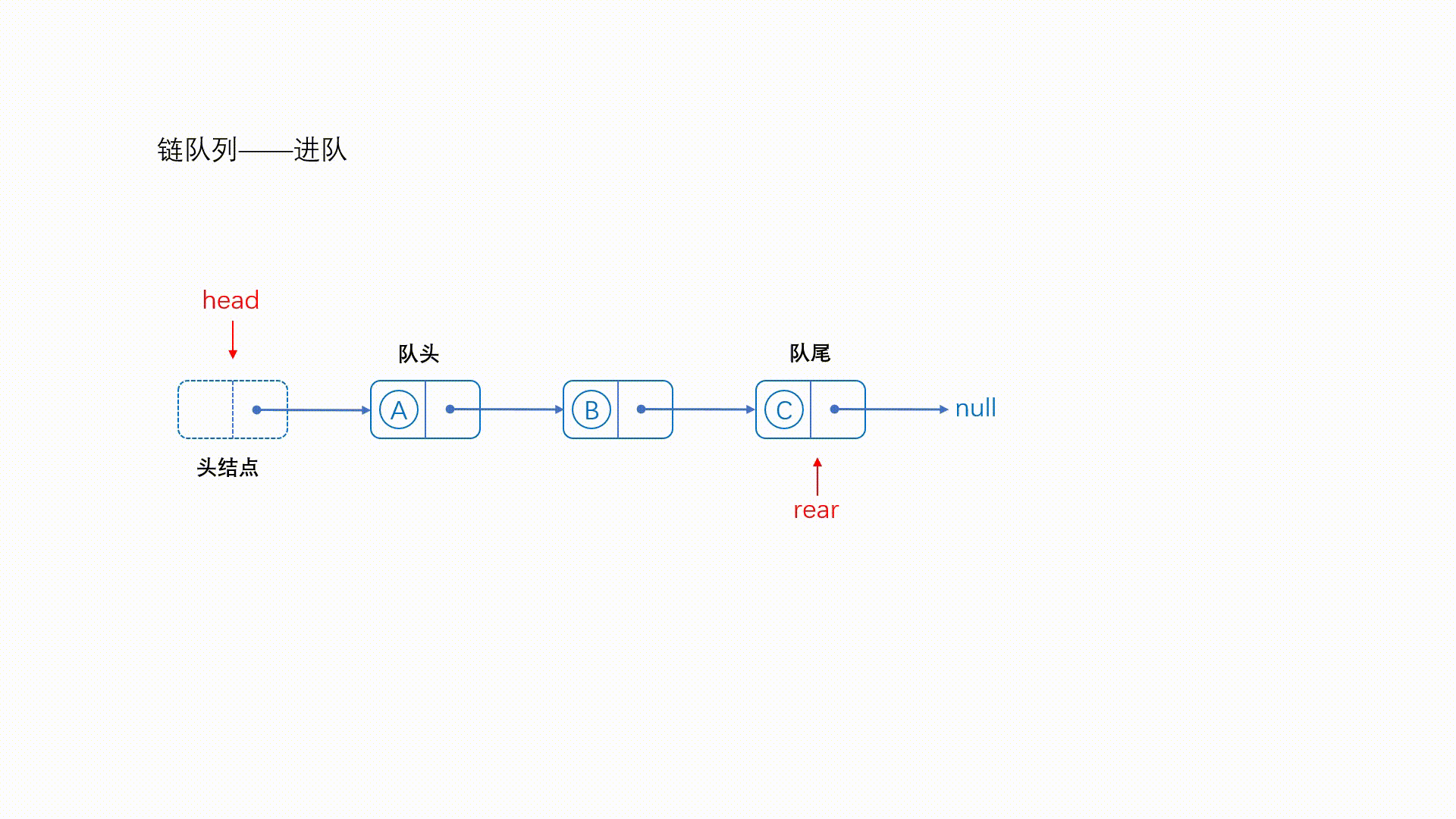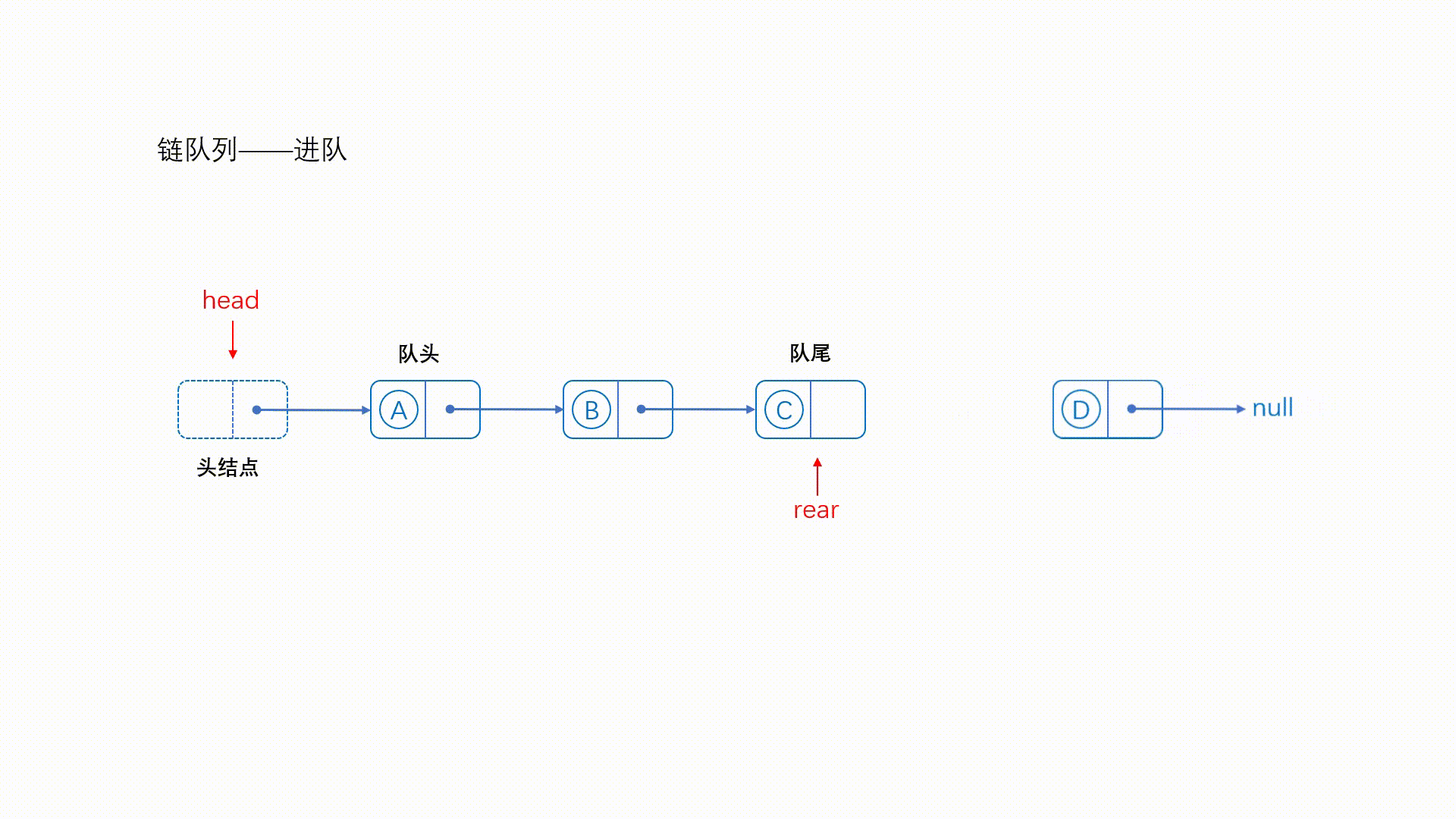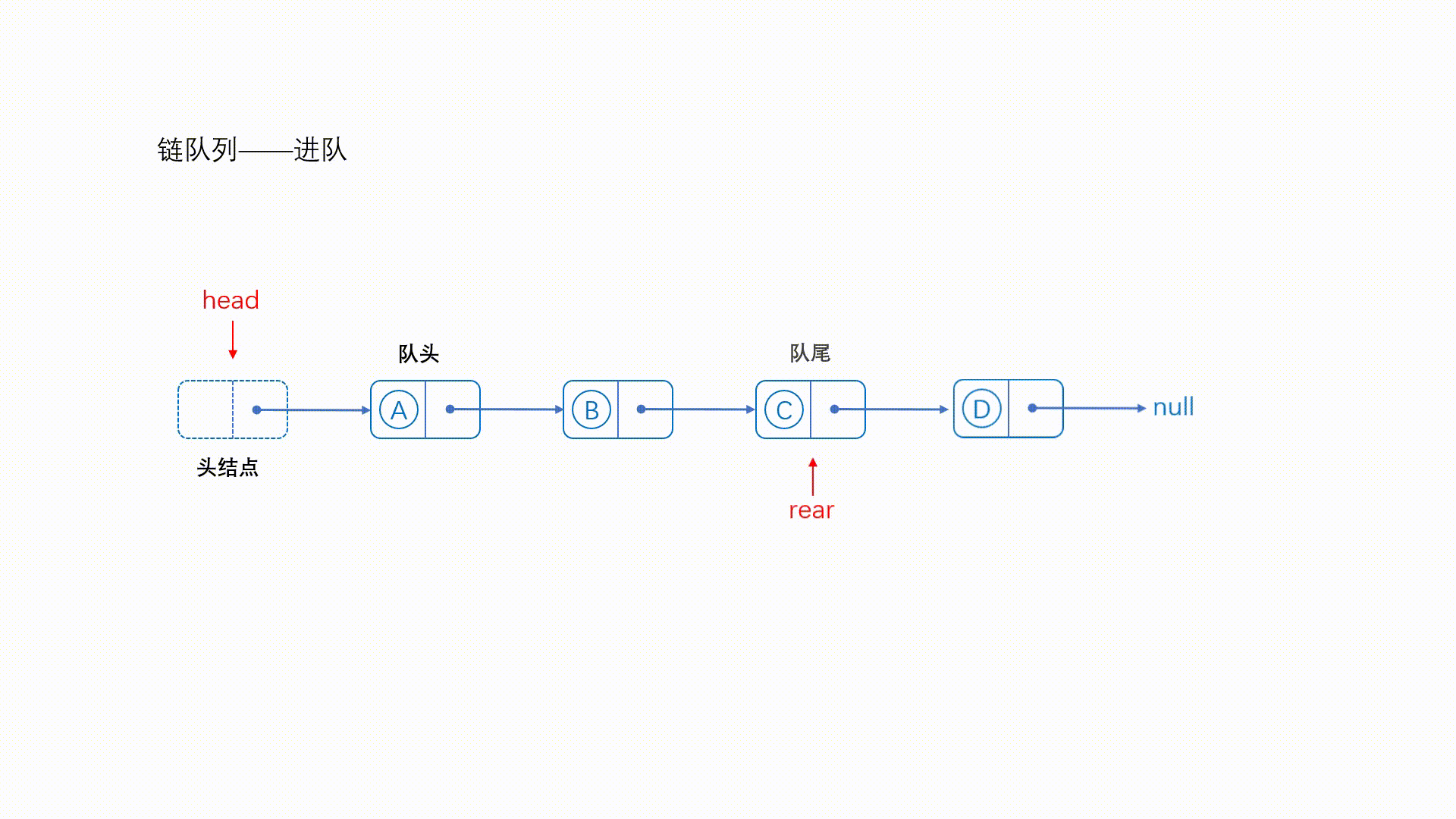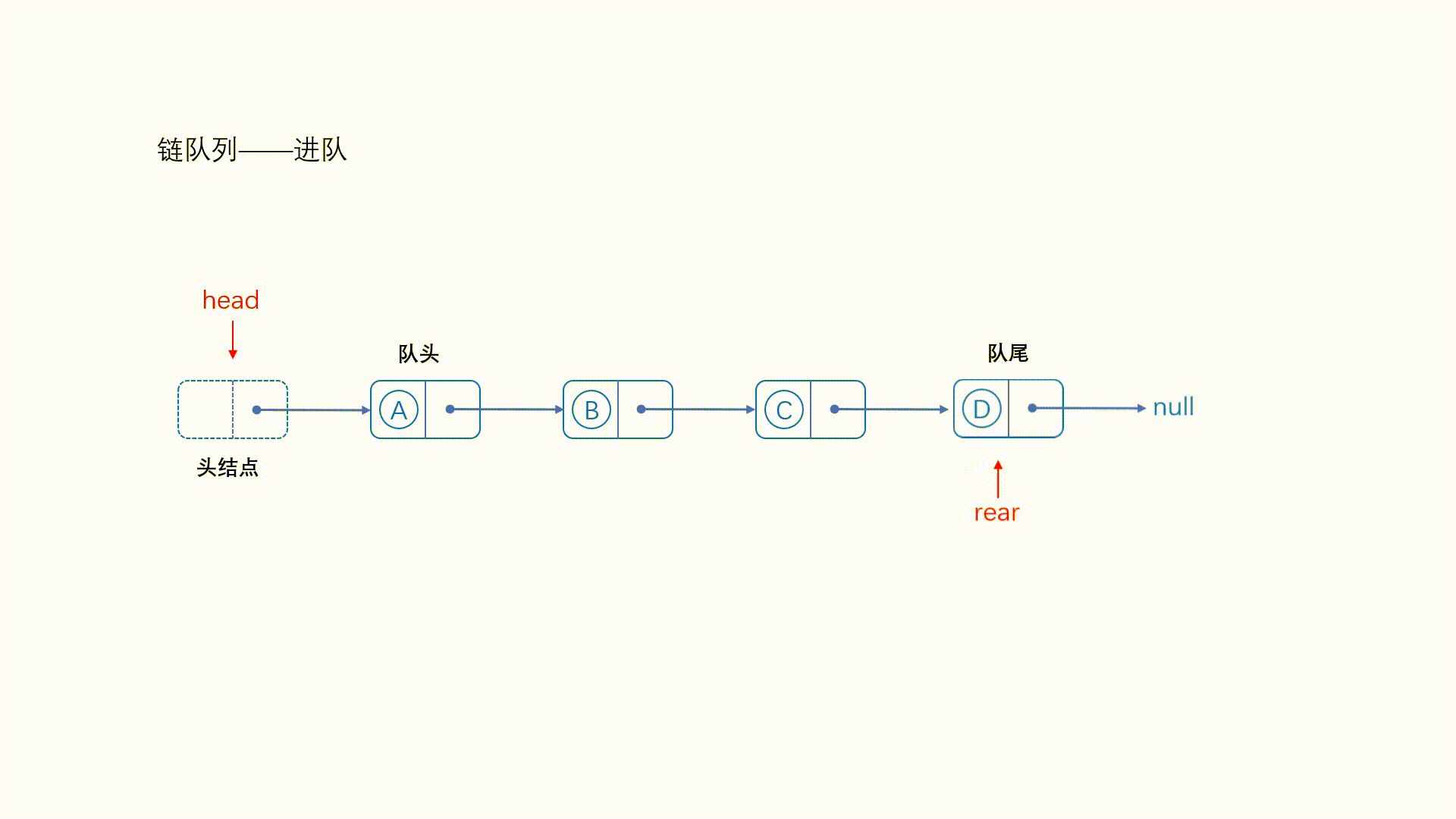
因为带有尾结点,所以很方便就能操作队尾元素了,直接将队尾的next指针指向新结点即可
来看一下动图?
//入队
void Push(Queue *q,int e){
Node *p = (Node *)malloc(sizeof(Node));
p->data = e;
p->Next = NULL;
q->rear->Next = p;
q->rear = p;
q->length++;
}2.3.3出队
由于带有头结点,所以直接将头结点的next指针指向队首元素的下一个结点即可
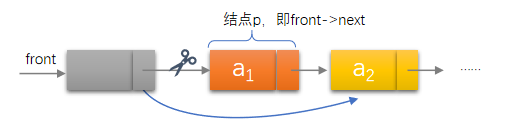
来看一下动图
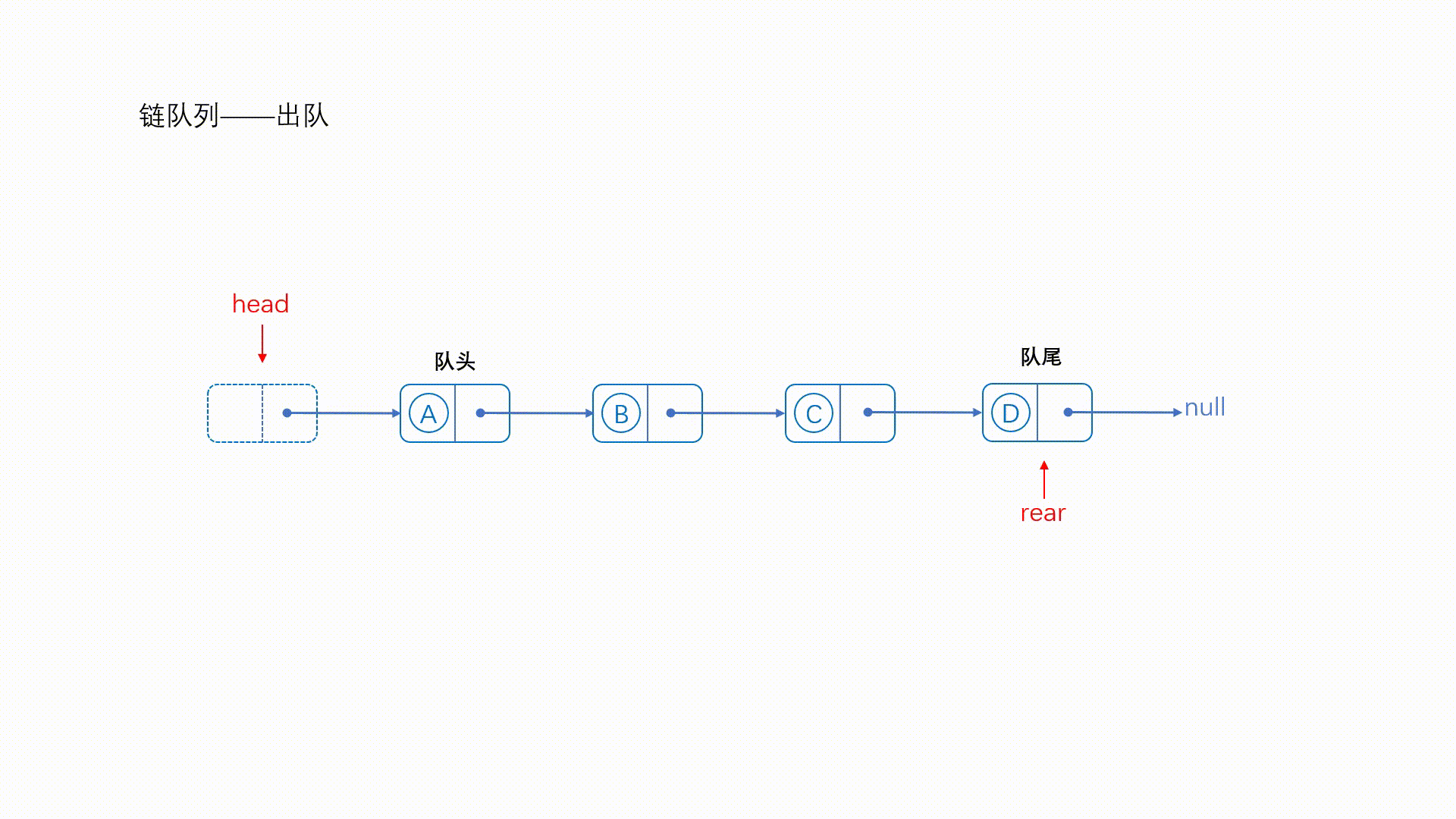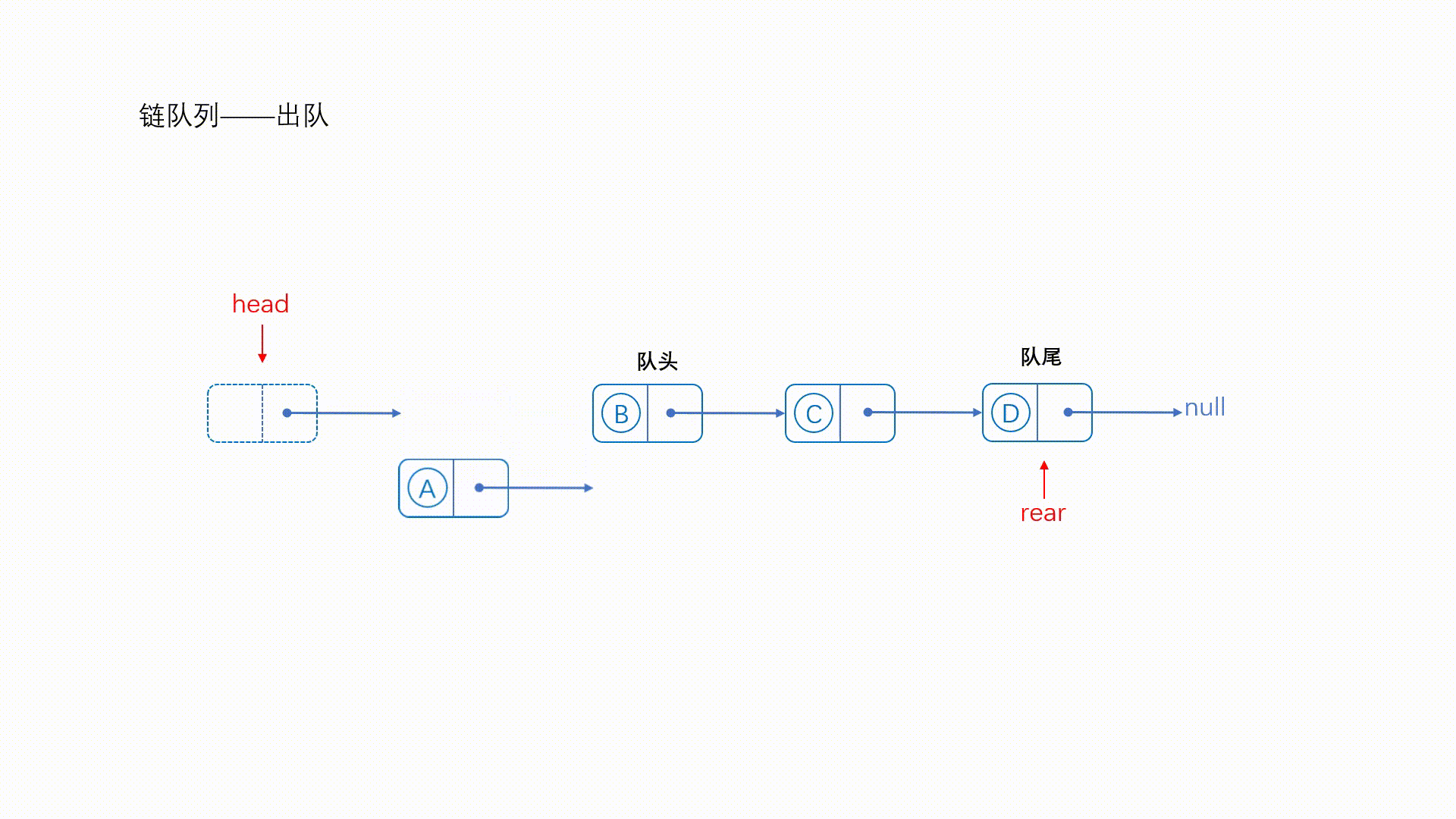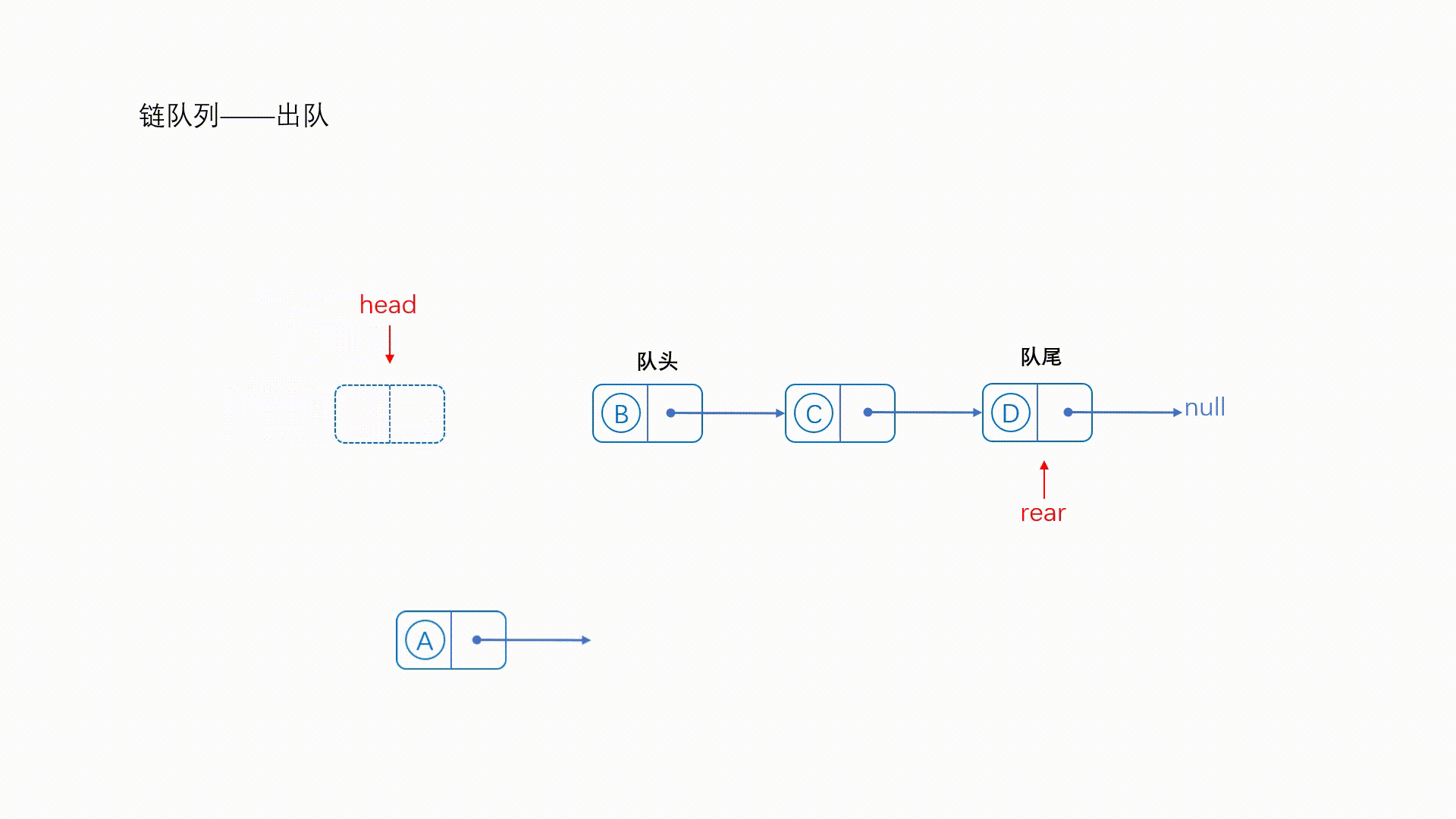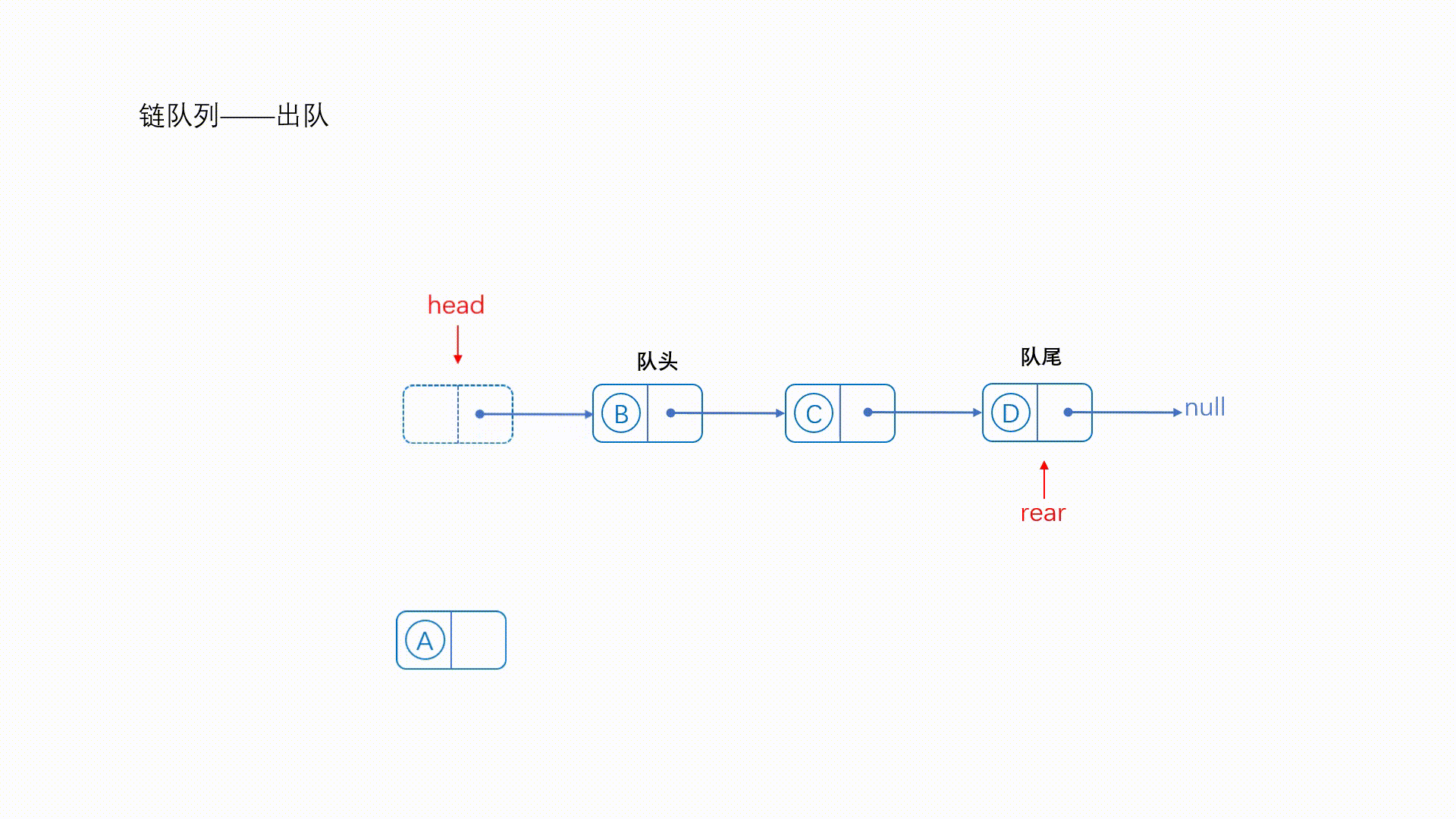
//出队
void Pop(Queue *q){
if(IsEmpty(*q)){
printf("队列空 出队失败~\n");
return;
}
Node *p = q->front->Next;
printf("%d出队成功\n",p->data);
q->front->Next = p->Next;
free(p);
q->length--;
}2.3.4链队列打印
和单链表的情况一样,只需判断是否为空,然后依次取data的值,再进行next的操作
//打印
void Print(Queue q){
if(IsEmpty(q)){
printf("队列空\n");
return;
}
Node *p = q.front->Next;
while(p != NULL){
printf("%d ",p->data);
p = p->Next;
}
printf("\n");
}2.3.5链队列完整代码
#include<stdio.h>
#include<iostream>
#include<math.h>
using namespace std;
//链队列的实现
//结点的存储结构
typedef struct Node{
int data;
struct Node *Next;
}Node;
//链队列的存储结构
typedef struct Queue{
Node *front,*rear;
int length;
}Queue;
//初始化
void Init(Queue *q){
q->front = (Node *)malloc(sizeof(Node));
q->rear = q->front;
q->length = 0;
}
//判断空
int IsEmpty(Queue q){
if(q.length == 0)return 1;
return 0;
}
//入队
void Push(Queue *q,int e){
Node *p = (Node *)malloc(sizeof(Node));
p->data = e;
p->Next = NULL;
q->rear->Next = p;
q->rear = p;
q->length++;
}
//出队
void Pop(Queue *q){
if(IsEmpty(*q)){
printf("队列空 出队失败~\n");
return;
}
Node *p = q->front->Next;
printf("%d出队成功\n",p->data);
q->front->Next = p->Next;
free(p);
q->length--;
}
//获取长度
void Length(Queue q){
printf("当前队列长度为:%d\n",q.length);
}
//打印
void Print(Queue q){
if(IsEmpty(q)){
printf("队列空\n");
return;
}
Node *p = q.front->Next;
while(p != NULL){
printf("%d ",p->data);
p = p->Next;
}
printf("\n");
}
int main(){
Queue q;
Init(&q);
Print(q);
Push(&q,1);
Push(&q,2);
Push(&q,3);
Push(&q,4);
Length(q);
Print(q);
Pop(&q);
Print(q);
return 0;
}三、内容总结
栈(stack)是限定仅在表尾进行插入和删除的线性表
队列(queue)是仅允许在一端进行插入操作,在另一端进行删除操作的线性表
它们均可以用线性表的顺序村粗结构来实现,但都存在着顺序存储的一些弊端
同时也都可以通过链式存储结构来实现,实现原则上与线性表基本相同
关于栈和队列还有独特的用处,例如利用栈来实现前中后缀表达式的转换和计算、以及括号匹配问题