目录
📔 前言
数据结构与算法如今在工作面试中占很高的比重,为了学好算法,大多数人都会去看各种书籍与视频,然后去做题,以做leetcode为例,没学算法前,你可能可以做些简单题,中等题也会一部分,学过数据结构与算法后,你可能发现自己会的中等题变多了,但依然有许多题无从下手,想暴力可时间过不了,此类情况就是无法将所学结合起来,没想到能用学过的方法解题,接下来,我们就来通过题目,剖析异或与二分。

📘 异或
异或作为位运算的一种,其运算方法为:相同(1与1,0与0)为0,相异为1
📑 例题引入
交换两个整数a,b 不能创建其他变量
void swap(int *a,int *b)
{
a^=b;
b^=a;
a^=b;
}代码很简单,异或就能解决,那么我们先来剖析一下怎么实现的
首先,我们要了解一些知识:异或是满足交换律和结合律的即:
a^b==b^a; (a^b)^c==a^(b^c);然后,一个数异或0为这个数本身,异或自生则为0
a^0==a; a^a==0;这个本身指的不是数字相同,而是开辟的空间相同,故只要开辟的空间不一样,那么异或后就不会为0.
a^=b ——> a=a^b
b^=a——>b=b^a^b——>b=b^b^a=a
a^=b——>a^b^a——>a^a^b——>=b
以上便是交换的
过程,了解了这些知识,接下来我们便可以做更多类型的题

📜 练习巩固
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1] 输出: 1
示例?2:
输入: [4,1,2,1,2] 输出: 4
?此题用异或计算非常简单,异或数组,因为交换律二次的异或后都为0,只剩出现一次的数,奇偶也是此方法,如一个数出现了奇数次,其他数出现了偶数次
int singleNumber(int* nums, int numsSize){
int j=0;
for(int i=0;i<numsSize;i++)
{
j^=nums[i];
}
return j;
}给定一个整数数组?nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按?任意顺序?返回答案。
进阶:你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现?
示例 1:
输入:nums = [1,2,1,3,2,5] 输出:[3,5] 解释:[5, 3] 也是有效的答案。
示例 2:
输入:nums = [-1,0] 输出:[-1,0]
示例 3:
输入:nums = [0,1] 输出:[1,0]
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* singleNumber(int* nums, int numsSize, int* returnSize){
long long num=0;long long num1=0;
int *arr=(int*)malloc(sizeof(int)*2);
for(int i=0;i<numsSize;++i)
{
num^=nums[i];
}
long long num2=num;
num1=num&(~num+1);
for(int i=0;i<numsSize;++i)
{
if((num1&nums[i])!=0)
num^=nums[i];
}
num2^=num;
arr[0]=num;arr[1]=num2;
*returnSize=2;
return arr;
}?要解决此题当然也是通过异或数组,接下来,我们通过代码来剖析方法:
前半段代码异或数组
for(int i=0;i<numsSize;++i) { num^=nums[i]; }此时得到的是两个出现一次元素的异或且num肯定大于0,接下来这行便有意思了
long long num2=num; num1=num&(~num+1);这行什么意思呢?我们画图理解:
?知道这个可能部分人就能想出来为什么要这么做了,不知道也没关系,我们继续剖析
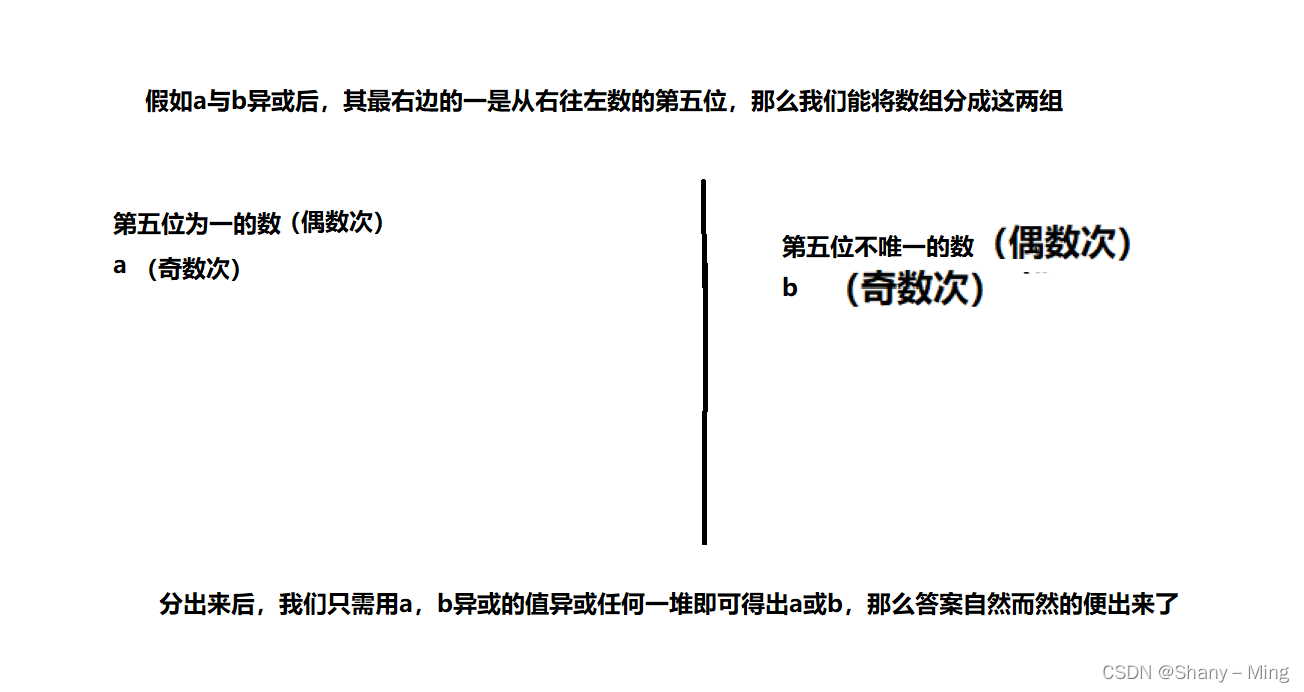
for(int i=0;i<numsSize;++i) { if((num1&nums[i])!=0) num^=nums[i]; }这段代码其实是在做区分,前边说了,两个出现一次的数异或其结果必不是0,那么,我们便找到其最右边的一(上一步),把整个数组分为两部分:一部分是这位上含一的,一部分是不含一的

📒 二分法
? 相信二分法大家早就很熟悉了,学习编程语言的时候我们就学习过二分法,但做题时可能会遗忘这种方法

📕 例题引入
给定一个有序数组,找到其中指定的数,返回其下标
#include<stdio.h>
void erfen(int a[],int b,int sz)
{
int left=0;
int right=sz-1;
while(left<right)
{
int mid=(left+right)/2;
if(b>a[mid])
left=mid+1;
if(b<a[mid])
right=mid-1;
else
{printf(“找到了下标为%d\n”,mid);
break;}
}
if(left>right){
printf(“找不到”);
}
int main()
{
int b=0;
printf(“请输入1~10间的一个数\n”);
scanf("%d",&b);
int a[]={1,2,3,4,5,6,7,8,9,10};
int sz=sizeof(a)/sizeof(a[0]);
void erfen(a,b,sz);
return 0;
}
?定义两个变量记录每次分的左右端,让其中间值与数进行比较,直到出现指定数或无法再分,时间复杂度为
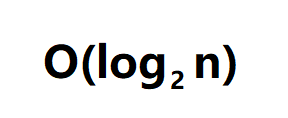
大家都懂,就不过多赘述了。
📰 练习巩固
1.
给定一个有序数组,如1,1,1,2,2,2,3,3,3,4,4,4,5,5,5
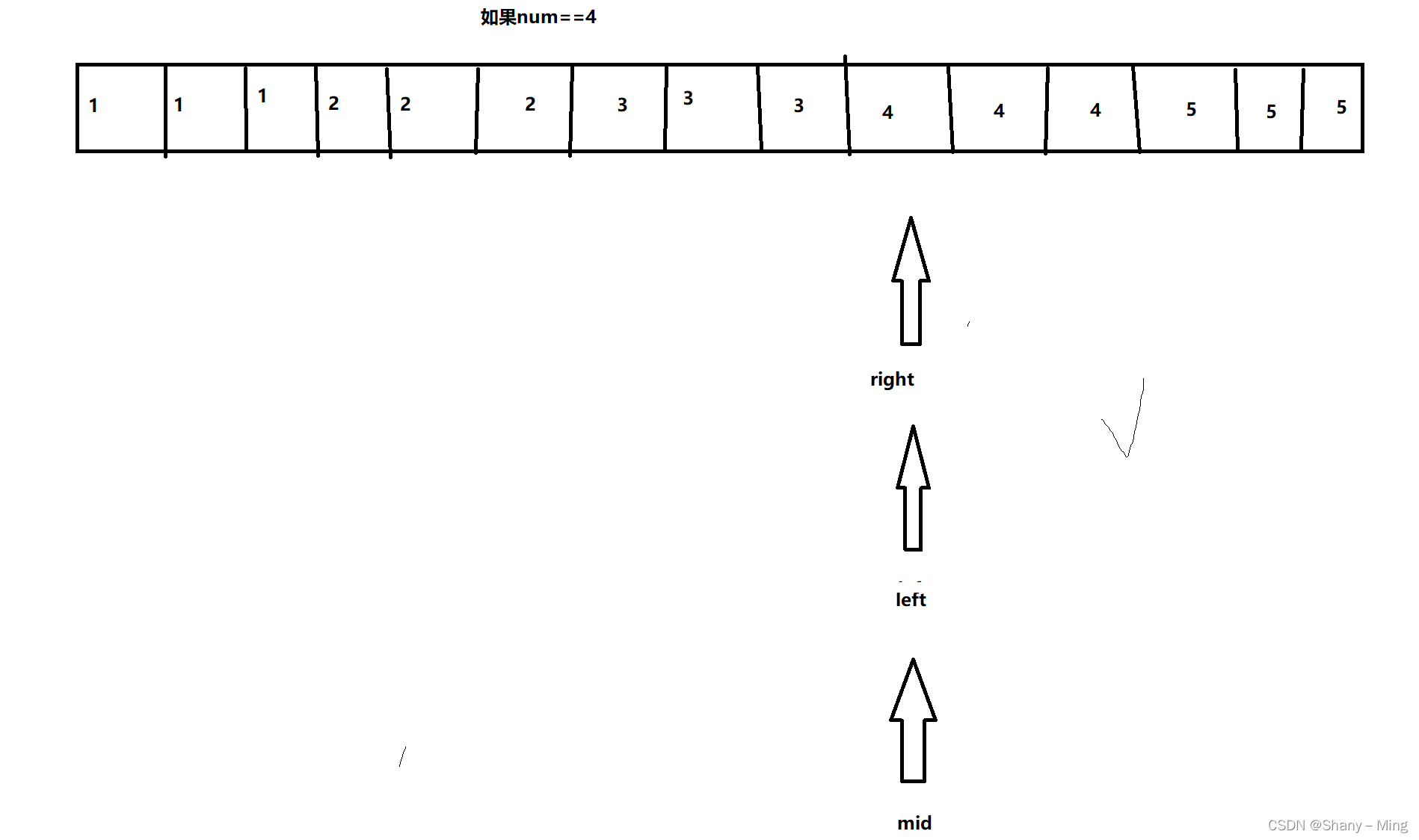
给定一个num,输出大于等于num最左侧的值或者小于等于num最右侧的值的下标。
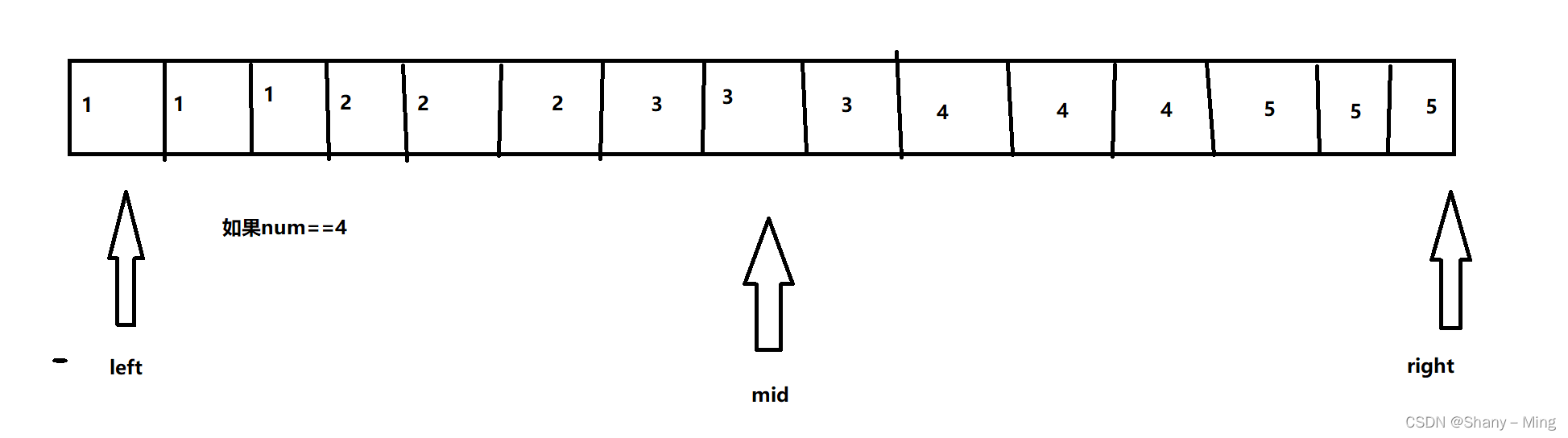
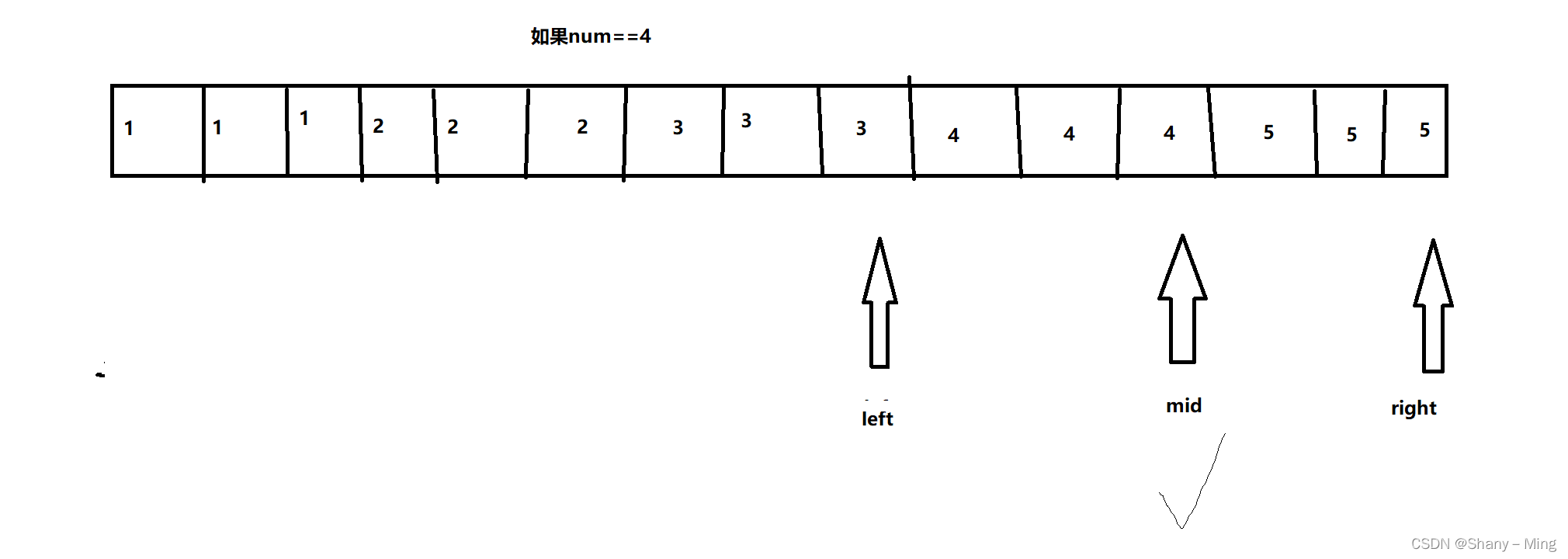
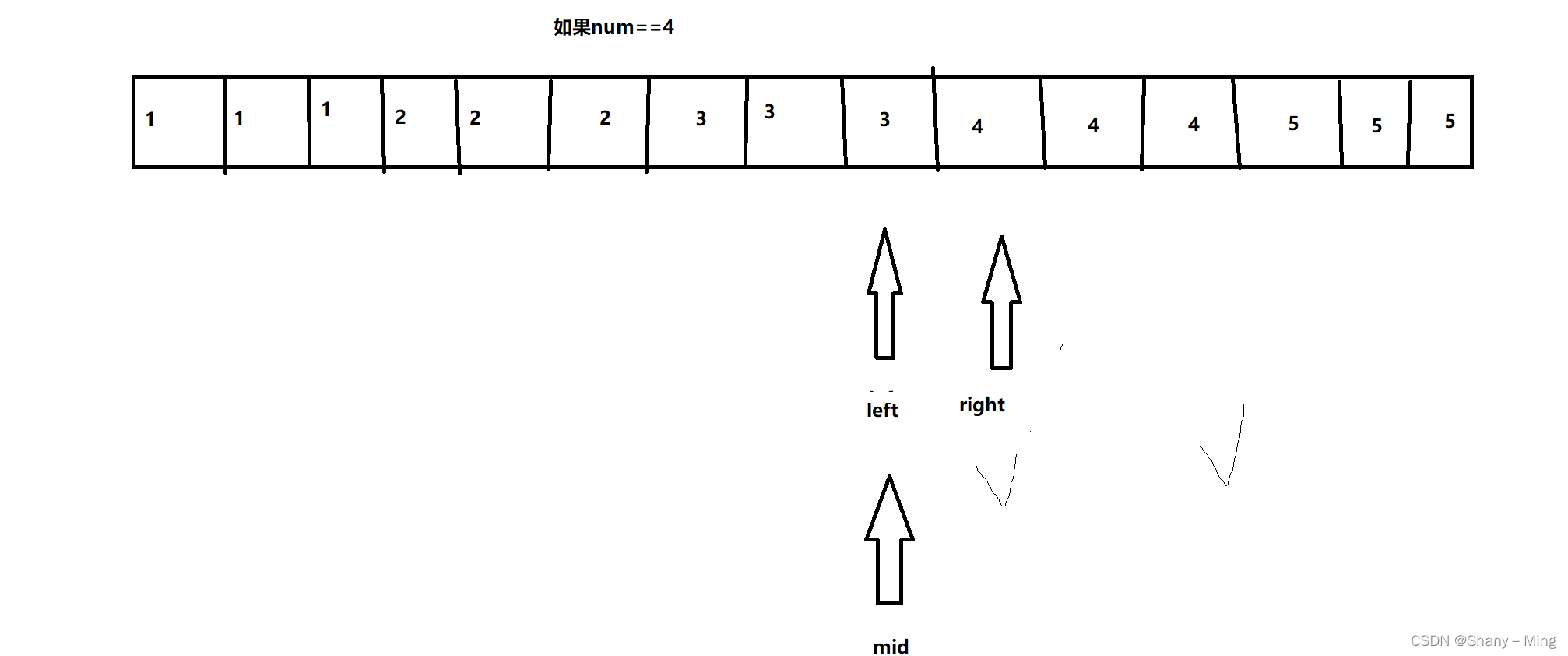
假如num=3,大于等于最左侧的下标为6,小于等于最右侧的下标为8,可以二分直到二分结束
没找到例题,就用这个吧(这题我们就用最左侧吧)
?
?用一个变量记录打勾的下标(即等于num的坐标,比较最小值进行替换)
?这便是此题的解题思路,当然你也可以暴力求解复杂度O(N),二分法则是O(logN)。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int main()
{
int num;
int arr[] = { 1,1,1,2,2,2,3,3,3,4,4,4,5,5,5 };
scanf("%d", &num);
int left = 0,count=14,mid=0;
int sz = sizeof(arr);
int right = sz - 1;
while (left <= right)
{
mid = (left + right) / 2;
if (num < arr[mid])
{
right = mid - 1;
}
if (num > arr[mid])
{
left = mid + 1;
}
if (num == arr[mid])
{
right= mid - 1;
if (count > mid)
count = mid;
}
}
printf("%d", count);
}?2.局部最小
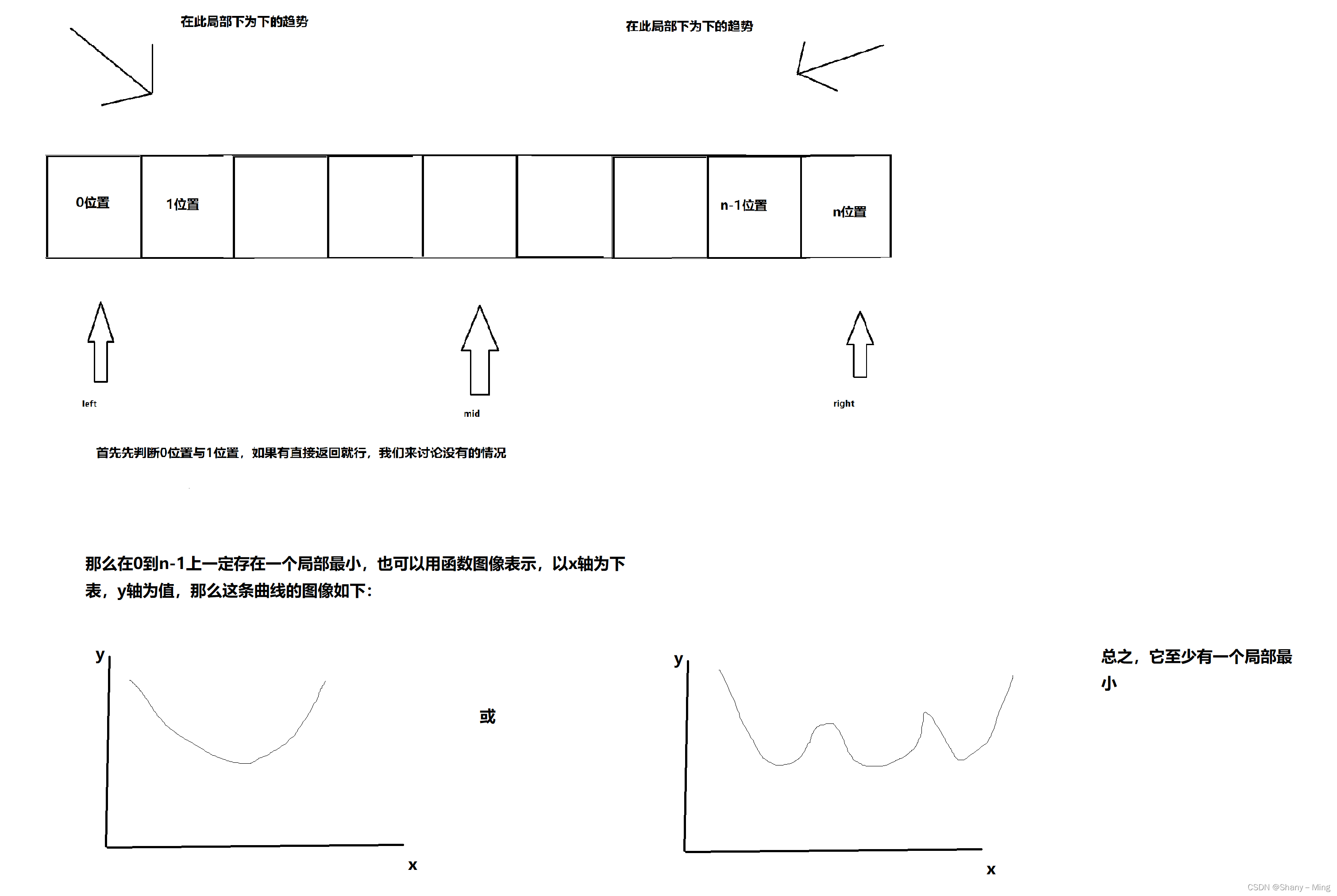
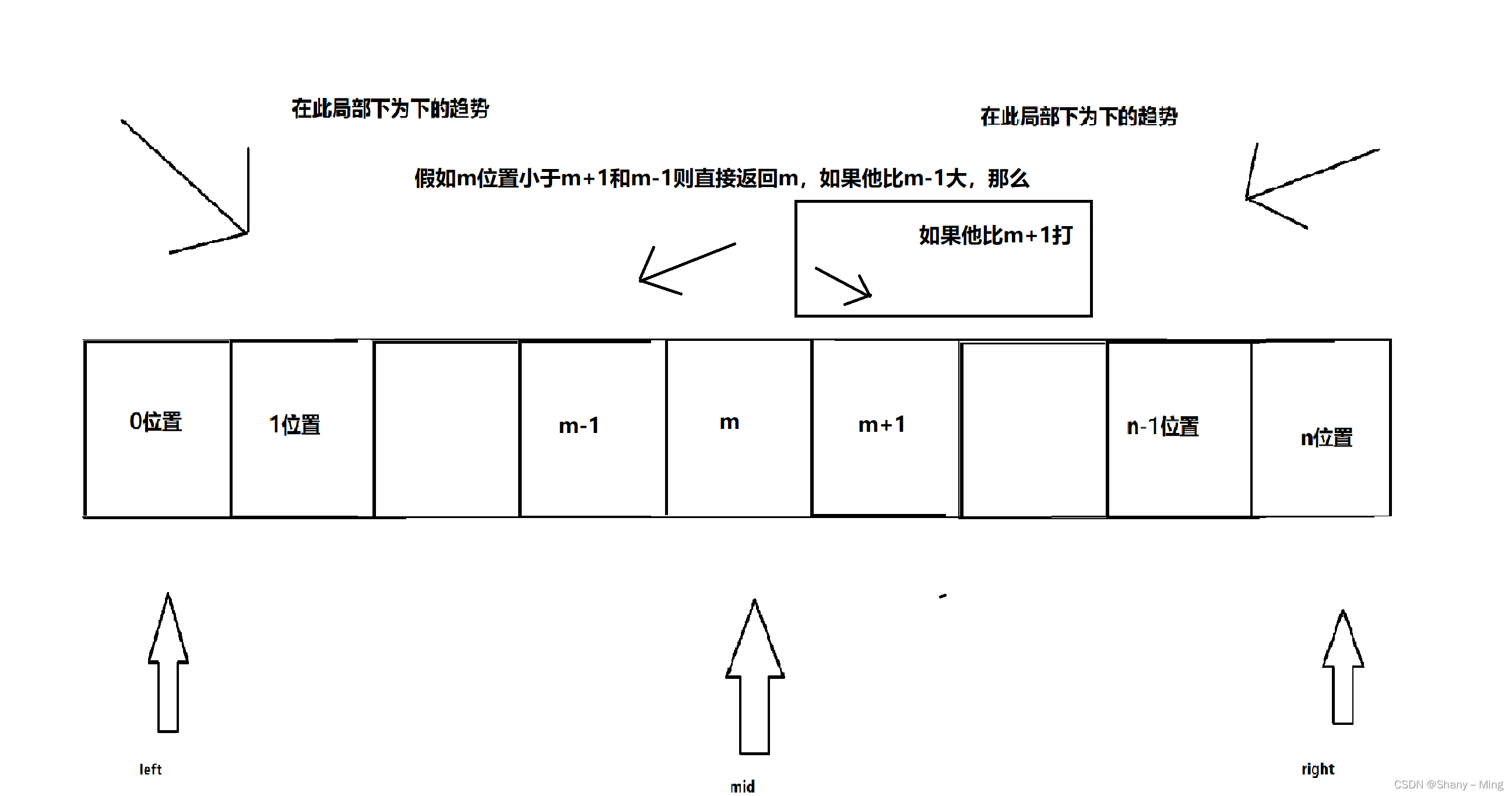
给定无序数组arr,且其中相邻两个数一定不相等,例如0位置上的数小于1位置上的数,那么0位置局部最小,如果n-1位置上的数比n-2位置上的数小,那么n-1就是局部最小,如果i<i-1且i<i+1,那么,i是局部最小。
思路如下:
?
?同样,也是一直二分直到结束
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组?nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回?任何一个峰值?所在位置即可。
你可以假设?nums[-1] = nums[n] = -∞?。
你必须实现时间复杂度为?O(log n)?的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例?2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;
? 或者返回索引 5, 其峰值元素为 6。
int findPeakElement(int* nums, int numsSize){
int left=0,right=numsSize-1;
while(left < right)
{
int mid = (left + right) / 2;
if(nums[mid] > nums[mid + 1])
right = mid;
else
left = mid+1;
}
return right;
}?📰 总结:
二分法可用于:
1.有序数组找下标
2.有序数组中大于等于一个值最左侧,小于等于这个值的最右侧下标
3.局部最小,局部最大
?