上一小节,讲到了二叉树的顺序存储和堆,这一小节来讲下二叉树的链式存储和一些相关的编程题。
二叉树的链式存储
链式存储的概念
链式存储和链表很像,可以说就是一种链表的变形。链式存储通过指针来相互连接和访问。
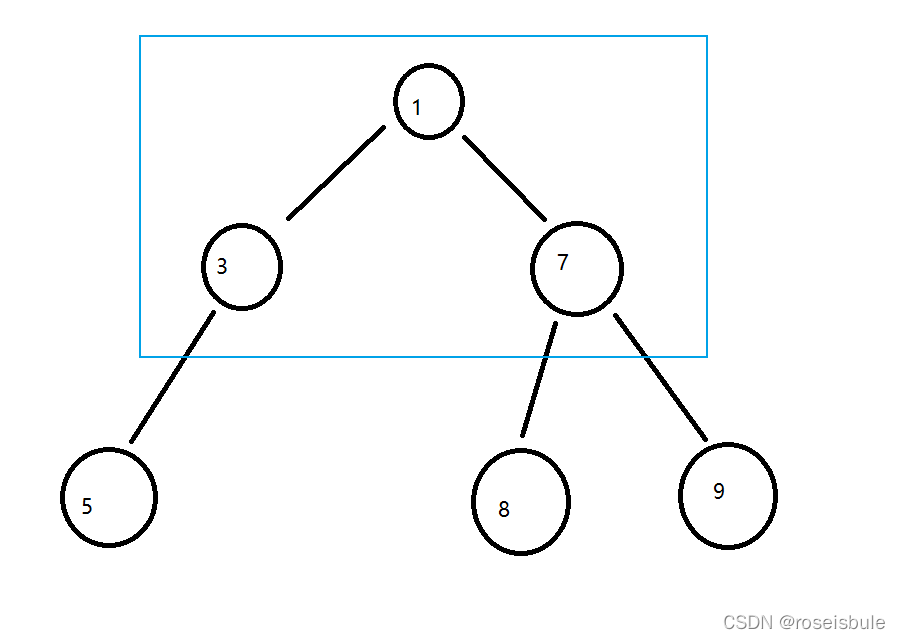
看上面这颗二叉树,可以看到每个节点都是要存储三个数据,左子节点,右子节点,自身值。所以我们可以把一个树的节点的结构体定义如下。
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;二叉树链式存储的函数
由于二叉树链式存储的创建是一个比较复杂的问题,所以二叉链的创建会在较后面讲到,先讲一些常用的函数。
二叉树节点个数的计算
如何来计算二叉链的节点个数呢?这是个难题,我们之前讲到的二叉树顺序存储结构体本身就已经包含了二叉树节点个数,但二叉链没有呀,咋算呢?
首先,我们来想想这样一个问题。假设,你是某个部门的领导,一天,你突然想知道你部门有多少人,要怎么算呢?你觉得你会自己一个个去算人头吗?应该是不会的吧。假设你的部门由两个办公处组成,那你应该是可以让这两个办公处去计算他们有多少人,然后把他们两个加起来再加上自己,这就是部门的人数了吧。那同样的,处长应该也不会自己亲自去算人头,而是下发给他的两个下级,和你是一样的想法。
 最后组长将自己的组员人数往上汇报,接着处长往上汇报给部长,部长把人数一加,就得到了部门的数量。这是不是和树的节点计算很像呀。
最后组长将自己的组员人数往上汇报,接着处长往上汇报给部长,部长把人数一加,就得到了部门的数量。这是不是和树的节点计算很像呀。
根节点向两子节点发送汇报命令,最后叶子节点不断往上汇报节点个数,从而就得到了整个树的节点个数。好的,说了这么多,就直接上代码吧。
// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
if (root == NULL)
return 0;
return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}?这种思路叫做分治,分而治之。将一个问题分为几个相同的子问题。可以看到,递归真的是简洁而优雅。
计算二叉树叶子节点的个数
这个就很上面的很像很像了,只不过要修改一下条件,当该节点为叶子节点时,则代表着左右子节点都为空。
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
计算二叉树第k层节点的个数
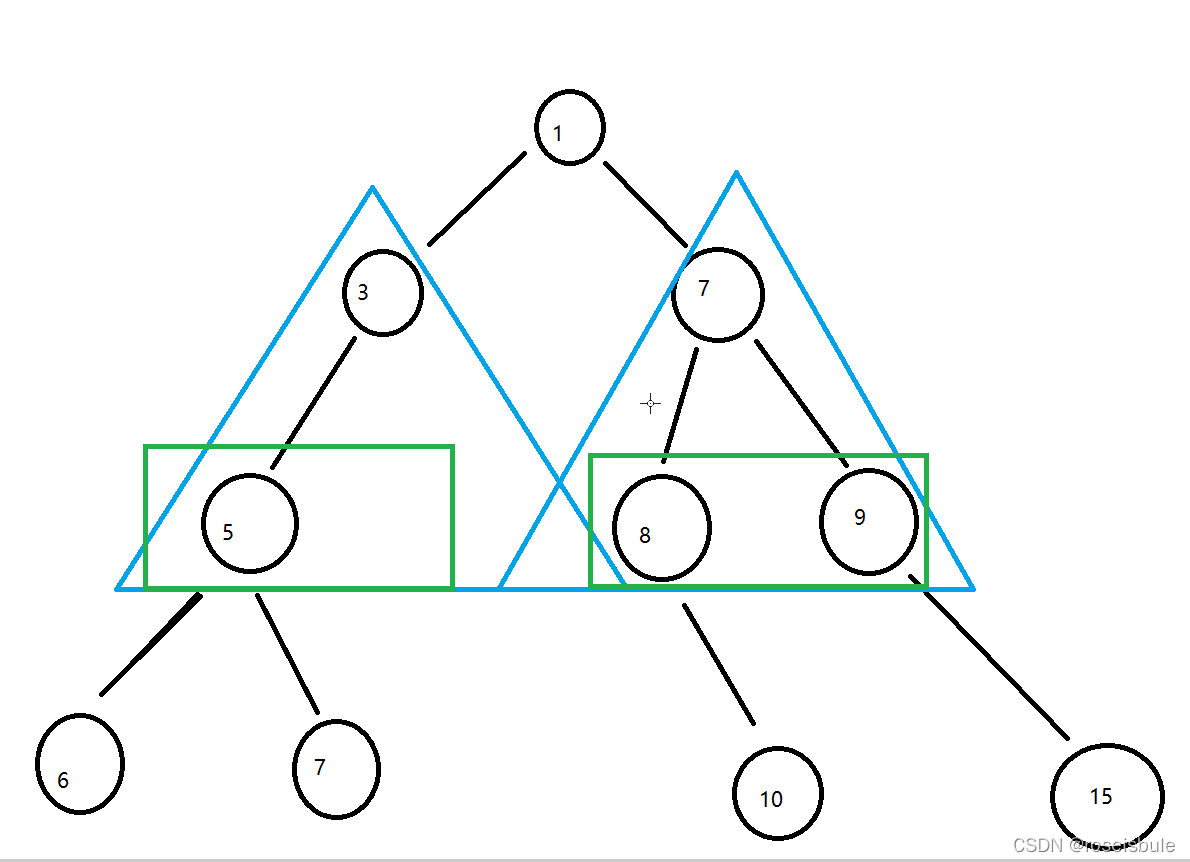
这个比上面的难度就是加大了,难在哪呢?其实都明白应该是要用分治来解决问题,但是可惜,这个分治不好找。我们再回想一下啥是分治。分治就是把大问题转化为相同的小问题,那什么是不变的呢?
第k层的节点是不变的。什么意思呢,就是不管别的这些节点在第几层,都是不变的。也就是说,如果我要计算第三层有多少节点,此时我要是把第二层而不是第一层看作根节点,那么问题就转化成了,第二层有多少节点。如果我把第三层看作根节点,那么问题就转化成了有多少个根节点。
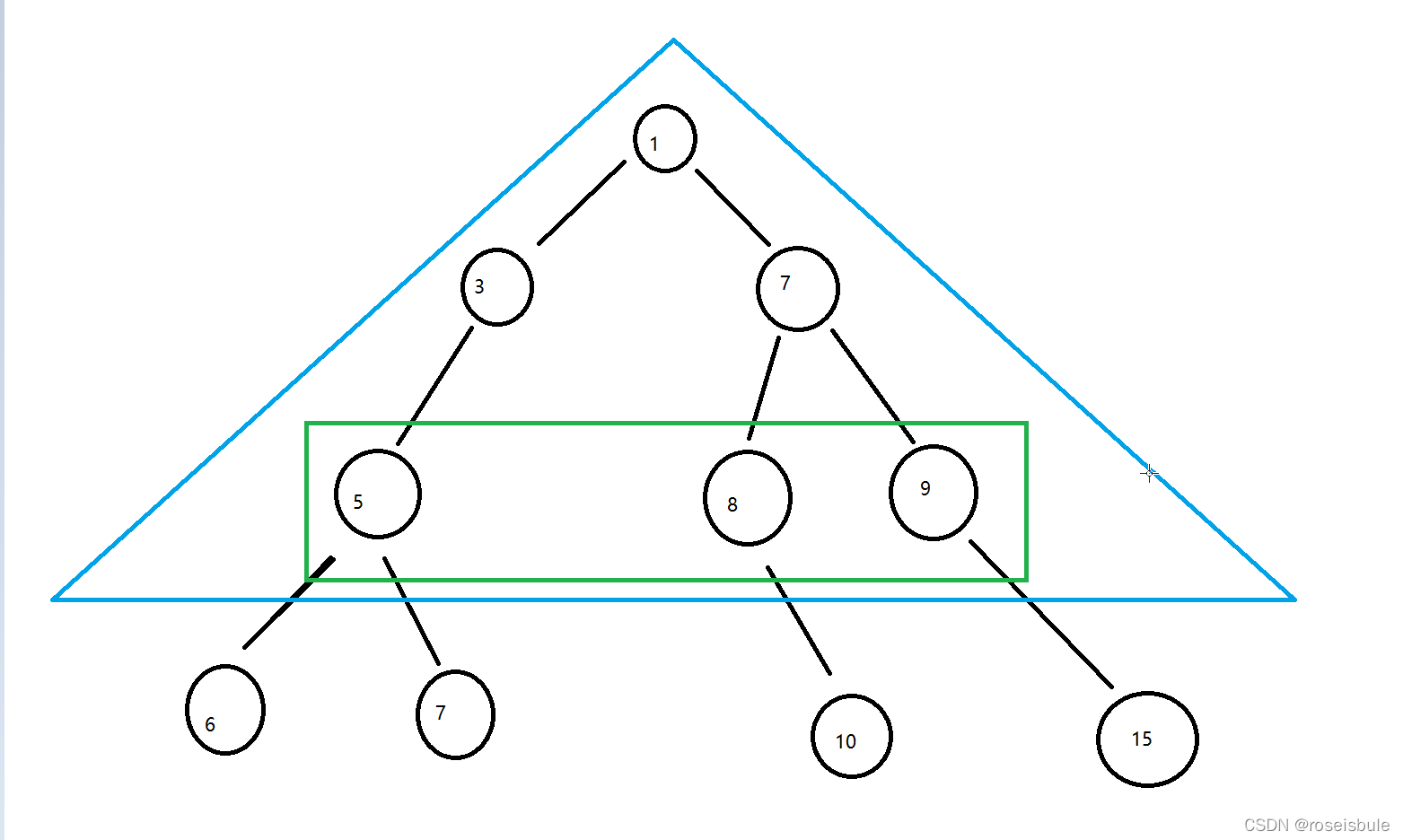
?
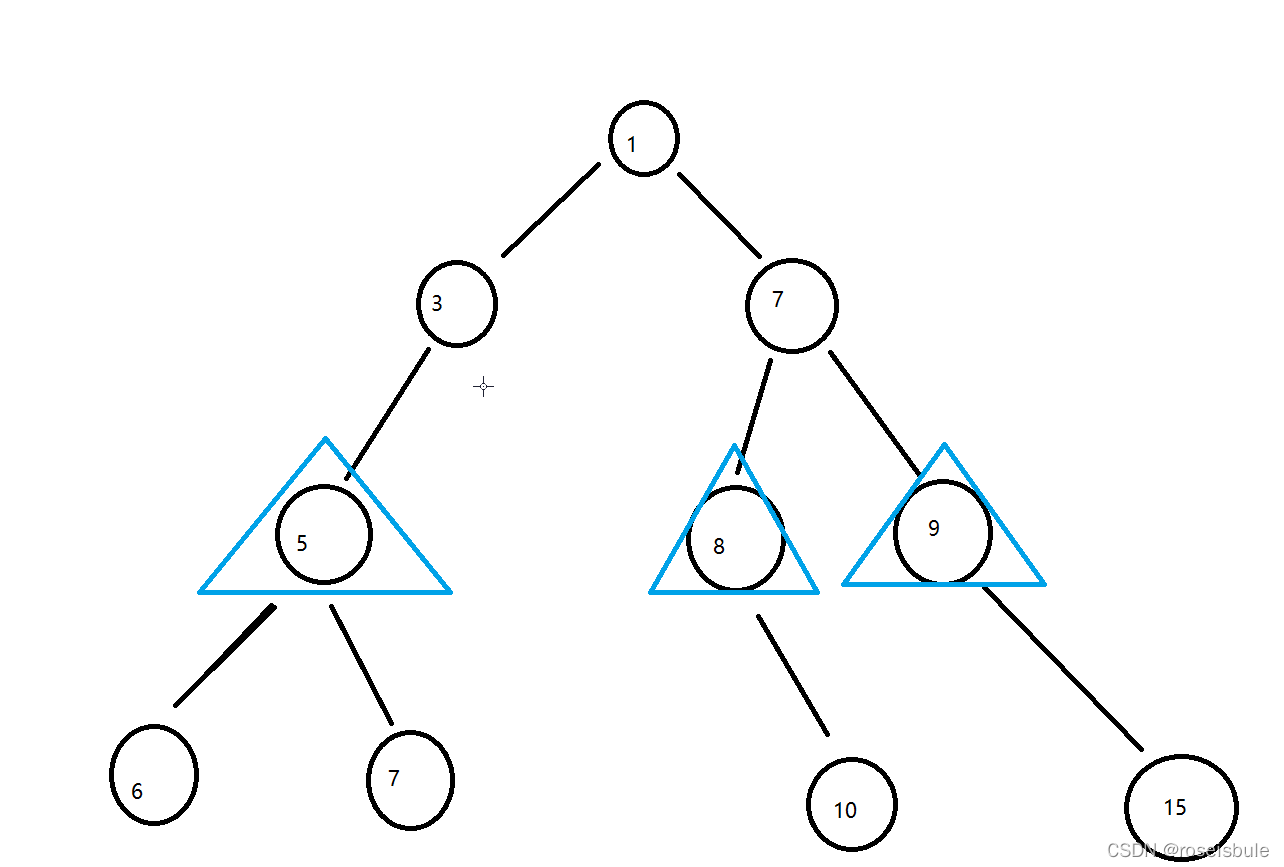
?如果是转化成了问有多少根节点,那么就太简单了,不为空就是+1,为空就是0。
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)
return 0;
if (k == 0)
return 1;
return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}查找值为k的节点
这个就和上面的部长算人问题很像了,改成了部长找人。部长把问题下发给处长,让他们在处里找人,找到了返回指针,找不到返回NULL。
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
return NULL;
if (root->data == x)
return root;
BTNode* tmp = BinaryTreeFind(root->left, x);
return tmp == NULL ? BinaryTreeFind(root->right, x) : tmp;
}二叉树的前序遍历
好了,上正菜了奥。遍历可以说是二叉链的精华了。
好的,让我们先来看看什么是前序遍历。简单的来讲就是先访问自己的值,再访问左子节点和右子节点的值,这就是前序遍历,等会还有中序和后序遍历,中序就是先访问左子节点,再访问自己,再访问右子节点。后序遍历就是把访问自己放在最后。
我们先不写代码,让我们来看看这棵树的前序遍历是什么样的。
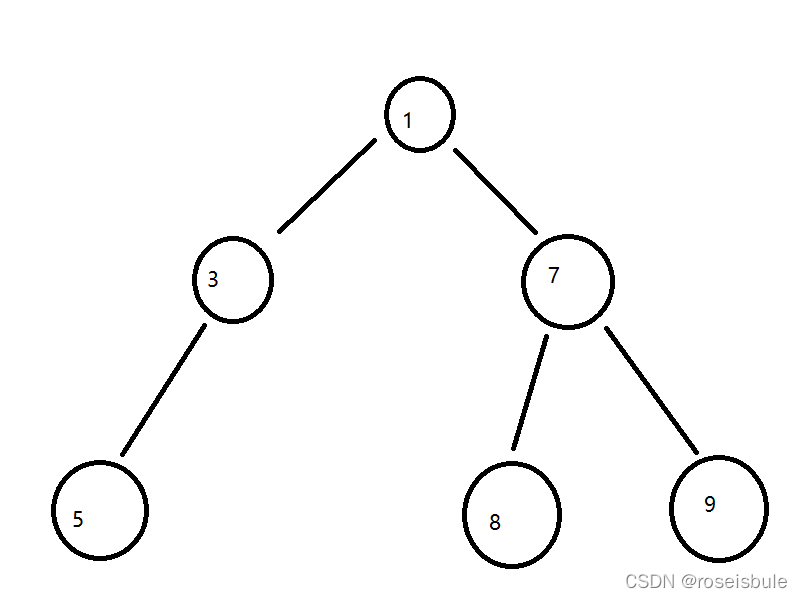
?从根节点开始,先访问自己再访问左子节点,再访问右子节点。
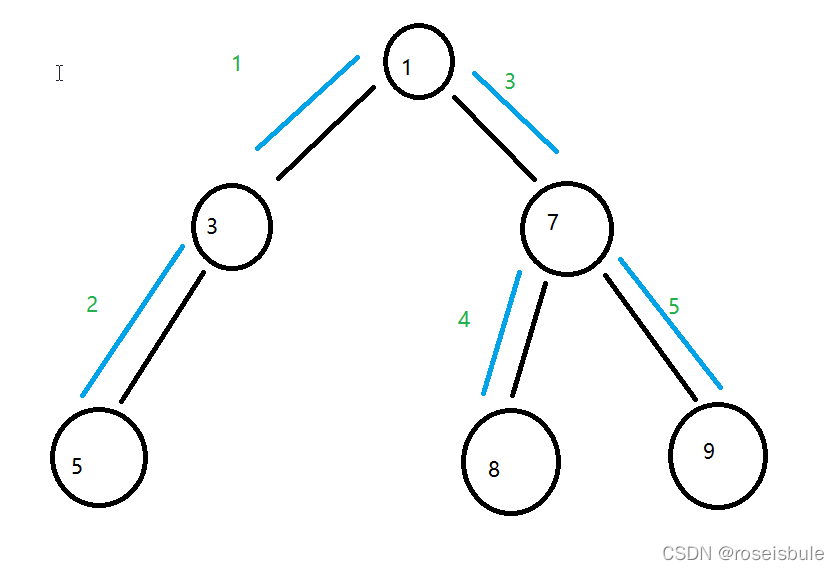
?由此得到的访问顺序是,1->3->5->7->8->9。
那么怎么用代码写出来呢?
还得是分治。
我们来看一下,对于一个节点来说,前序代表着先访问自己的值,再访问左右子节点,对于每一个节点都是这样的。
所以,代码很快就能出来了。
// 二叉树前序遍历
void BinaryTreePrevOrder(BTNode* root)
{
if (root == NULL)
return;
printf("%c ", root->data);
BinaryTreePrevOrder(root->left);
BinaryTreePrevOrder(root->right);
}二叉树的中序和后序
中序和后序其实和前序是一样的,只是换了个位置而已,所以就带过了。
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
if (root == NULL)
return;
BinaryTreeInOrder(root->left);
printf("%c ", root->data);
BinaryTreeInOrder(root->right);
}
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
if (root == NULL)
return;
BinaryTreePostOrder(root->left);
BinaryTreePostOrder(root->right);
printf("%c ", root->data);
}二叉树的层序遍历
这也是一个比较复杂的问题, 因为前面的前序等遍历都是深度优先,所以递归能很好地解决,但是层序就是广度优先地,他优先要访问一整层,然后访问下一层。

我们还是已这课树为例。访问顺序应该是 1->3->7->5->8->9。我们先来观察前面两层的遍历,1->3->7,也就是节点->左子节点->右子节点。然后再来观察后面两层的遍历,3->7->5->8->9,也就是节点1->节点2->1的左子节点->1的右子节点(NULL)->7的左子节点->8的右子节点。
观察分析两个遍历,我们发现如果当我遍历到某个节点时,我把他的左右子节点插入到访问顺序上,访问完这个节点后,把这个节点从访问顺序上删除,就可以完成层序遍历了。
那么现在又有一个问题了,这个访问顺序放哪呢?
显然当我们访问了某个节点时,把节点的左右子节点放入后,就要删掉对该节点的访问,先进先出,用列显然很合适。
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ROOT!\n");
return;
}
Queue tmp;
QueueInit(&tmp);
QueuePush(&tmp, root);
do
{
BTNode* x = QueueFront(&tmp);
if (x == NULL)
{
printf("NULL ");
}
else
{
printf("%c ", x->data);
QueuePush(&tmp, x->left);
QueuePush(&tmp, x->right);
}
QueuePop(&tmp);
} while (!QueueEmpty(&tmp));
printf("\n");
}二叉链的创建
好的,之前说到,二叉链的创建并不是一个简单的过程,像这道oj题,链接:二叉树遍历_牛客题霸_牛客网,就是关于二叉链的创建。从中我们可以看出,二叉链的创建是可以中序前序后序创建的,但是如果不按这些方法创建,很难说去分析这棵二叉树。
既然这道题目说的是用前序创建二叉树,那我们就按这种方法来,其实就是和前序遍历是差不多的,只是多了一个创建的过程。
这里给出关键函数
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
if (a == NULL)
return NULL;
if (a[*pi] != '\0' && a[*pi] != '#')
{
BTNode* root = NodeCreate(a[*pi]);
(*pi)++;
root->left = BinaryTreeCreate(a, pi);
(*pi)++;
root->right = BinaryTreeCreate(a, pi);
return root;
}
return NULL;
}
BTNode* NodeCreate(BTDataType x)
{
BTNode* tmp = (BTNode*)malloc(sizeof(BTNode));
if (tmp == NULL)
{
printf("Malloc Fail In NodeCreate\n");
exit(-1);
}
tmp->data = x;
tmp->left = NULL;
tmp->right = NULL;
return tmp;
}
二叉链的编程题
判断一个二叉树是否为完全二叉树
首先我们复习一下,什么是完全二叉树。完全二叉树就是在遇到空节点前,都没有空节点,且遇到空节点后,二叉树就结束了。
所以能清楚的一个点就是,我们需要用到层序遍历的思想,如果非最第底层的每一层都是满的,且最底层满足上面所说的,就是一颗完全二叉树。
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
if (root == NULL)
return true;
Queue tmp;
// 注意这里的列都存放的是节点的指针
QueueInit(&tmp);
QueuePush(&tmp, root);
do
{
// 层序遍历树
// 访问一个节点后 再放入节点左右子节点
// 然后删除该节点
BTNode* x = QueueFront(&tmp);
if (x == NULL) // 如果发现了空节点
{
if (QueueEmpty(&tmp)) // 如果发现列也是空的 代表遍历完毕
return true;
else
return false; // 否则说明 不是完全二叉树
}
else
{
QueuePush(&tmp, x->left);
QueuePush(&tmp, x->right);
}
QueuePop(&tmp);
} while (!QueueEmpty(&tmp));
return true;
}检查两颗树是否相同
链接:力扣
这个题目要进行对两个树判断,判断是否完全相同,那我们直接遍历一遍,然后逐个判断即可。
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
if (p == NULL && q == NULL)
return true;
if (p == NULL || q == NULL)
return false;
return p->val == q->val
&& isSameTree(p->left, q->left)
&& isSameTree(p->right, q->right);
}?对称二叉树
链接:力扣
这道题目和上面很像,只不过是判断翻转,那我们只要左孩子判断右孩子,右孩子判断左孩子即可。
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
if (p == NULL && q == NULL)
return true;
if (p == NULL || q == NULL)
return false;
return p->val == q->val
&& isSameTree(p->left, q->right)
&& isSameTree(p->right, q->left);
}
bool isSymmetric(struct TreeNode* root)
{
return isSameTree(root->left, root->right);
}另一颗树的子树
链接:力扣??????
这个题目非常地有意思。怎么判断子树呀。比如A中找B,那就遍历A,如果A的某个节点和B的根节点相同,那就代表A有可能会出现B,这是我们只要往下判断二树是否相同即可,简单吧。而且这个题目还给你加了个限制,这个A中的B一定在底端,就是说A中的B不会出现在A的中部,这样就可以放开地判断是否相等了。
bool isSameTree(struct TreeNode* rootleft, struct TreeNode* rootright)
{
if (rootright == NULL && rootleft == NULL)
return true;
if (rootright == NULL || rootleft == NULL)
return false;
return rootleft->val == rootright->val &&
isSameTree(rootleft->left, rootright->left) &&
isSameTree(rootleft->right, rootright->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
if (subRoot == NULL)
return true;
if (root == NULL)
return false;
return isSameTree(root, subRoot) || isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}但是如果我把这个问题改一下,A中的B可以出现在A的任意位置,而不只是底部,怎么办呢?
其实也不难,无非只是改一下子树相同的条件改一下而已。
bool isSameTree(struct TreeNode* rootleft, struct TreeNode* rootright)
{
if (rootright == NULL) // 如果subRoot为空了 说明判断完了 确实为子树
return true;
else
if (rootleft == NULL) // 如果subRoot不为空 但是Root为空了 那就没得判断了
return false;
return rootleft->val == rootright->val &&
isSameTree(rootleft->left, rootright->left)&&
isSameTree(rootleft->right, rootright->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{
if(subRoot == NULL)
return true;
if(root == NULL)
return false;
return isSameTree(root, subRoot) || isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}翻转二叉树
链接:力扣
这个题目也是很有意思的。
其实翻转这个东西吧,对于二叉链来讲,就是把两个孩子指针交换下即可。有人就说了,你为啥不交换节点的值呢?其实不需要的,因为我们从root开始,直接把两个指针一交换,管你是值还是什么,全都给你交换了。然后接着往下,利用分治递归思想,不停地交换,就完成了翻转。
struct TreeNode* invertTree(struct TreeNode* root)
{
if (root == NULL)
return NULL;
SwapTree(root);
return root;
}
void SwapTree(struct TreeNode* root)
{
if (root == NULL)
return;
struct TreeNode* left = root->left;
root->left = root->right;
root->right = left;
SwapTree(root->left);
SwapTree(root->right);
}最后
下一节,将数据结构的10种排序。
