[数据结构与算法]【算法每日一练】——买卖股票的最好时机

💻个人简介

• ??作者简介： 大家好，我是〖雪月清〗 ??
• 🎉个人主页：〖雪月清〗🌸
• 📣算法每日一练：带你感受算法百态?

🚩一、买卖股票的最好时机(一)

原题传送门

🏳??🌈1.题目描述

假设你有一个数组prices，长度为n，其中prices[i]是股票在第i天的价格，请根据这个价格数组，返回买卖股票能获得的最大收益

1.你可以买入一次股票和卖出一次股票，并非每天都可以买入或卖出一次，总共只能买入和卖出一次，且买入必须在卖出的前面的某一天

2.如果不能获取到任何利润，请返回0

3.假设买入卖出均无手续费

数据范围： 0≤n≤ 10^5 , 0≤val ≤10^4

要求：空间复杂度 O(1)，时间复杂度 O(n)

示例：

输入：

[8,9,2,5,4,7,1]

返回值：

5

说明：

在第3天(股票价格 = 2)的时候买入，在第6天(股票价格 = 7)的时候卖出，最大利润 = 7-2 = 5 ，不能选择在第2天买入，第3天卖出，这样就亏损7了；同时，你也不能在买入前卖出股票。

🏳??🌈2.题目分析

由题目描述可知，我们是求给定数组prices 中 prices[j] - prices[i] 的最大值，但是必须保证 j > i

最容易想到暴力法，使用两层循环，并使用一个变量max来记录后面 - 前面的最大值,代码如下：

import java.util.*;
public class Solution {
    /**
     * 
     * @param prices int整型一维数组 
     * @return int整型
     */
    public int maxProfit (int[] prices) {
        
        //记录最大值，初始值为0
        int max = 0;
        
        int n = prices.length;
        
            //遍历数组记录所遍历过的价格的最小值  
        for(int i = 0;i < n; i++){
            
          for(int j = i+1; j< n;j++){
              if(prices[j] > prices[i]){
                  max = Math.max(max,prices[j] - prices[i]);
              }
          }
            
        }
        
        return max;
        
    }
}

时间复杂度为O(N^2)，提交后发现超时，排除暴力法

思路1：动态规划

既然暴力法超时，那我们就想办法降低算法的时间复杂度，最常用的就是动态规划来降低时间复杂度。由于题目要求只能买卖一次，因此对于每天来说有两种状态 持有股票 没有持有股票

dp[i][0] //表示第 i+1天没有持有股票  (i是从0开始)
dp[i][1] //表示第 i+1天持有股票  

推导状态转移方程：

• 对于dp[i][0] 可能有两种情况：

1. dp[i-1][0] 前一天没有持有股票，当天也不购买股票

2. dp[i-1][1] +prices[i] 前一天持有股票，当天卖出

dp[i][0] 就是 两种情况的最大值

• 对于dp[i][1] 有两种情况：

1. 由于只能买卖一次，所以当天购买股票就是 -prices[i]

2. 前一天持有股票，当天不进行任何操作 dp[i-1][1]

dp[i][1] 就是 两种情况的最大值

 //动态转移方程
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1] + prices[i]);
            
 dp[i][1] = Math.max(-prices[i],dp[i-1][1]);

结果是最后一天不持有股票的值 dp[n-1][0]

思路2：贪心（一次遍历）

因为我们在卖出股票之前必须先买入，所以我们可以使用一个变量 min 记录下之前所有天股票的最低价格，使用另一个变量max记录到当前为止最大收益，然后每遍历到一天就计算 这一天如果卖出股票所获得收益 并与max比较更新max

   //每次使用当天的价格减去之前天数的最小价格 更新max
max = Math.max(max,prices[i] - min);
            
 min = Math.min(min,prices[i]);

🏳??🌈3.代码实现

动态规划 代码实现：

import java.util.*;


public class Solution {
    /**
     * 
     * @param prices int整型一维数组 
     * @return int整型
     */
    public int maxProfit (int[] prices) {
         
        int n = prices.length;
        
        //下标i是从0开始
        //dp[i][0] 表示第i+1天不持有股票 从第一天到第i+1天的收益
        //dp[i][1] 表示第i+1天持有股票 从第一天到第i+1天的收益
      int[][] dp = new int[n][2];
        //初始化第一天不持有股票的收益0
        dp[0][0] = 0;
        //初始化第一天持有股票的收益 就是第一天买了当天的股票 -prices[0]
        dp[0][1] = -prices[0];
       
        //从第二天开始
        for(int i = 1;i < n; i++){
            
            dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1] + prices[i]);
            
            dp[i][1] = Math.max(-prices[i],dp[i-1][1]);
        }
        
        //最后一天不持有股票此时的值就是最大收益
        return dp[n-1][0];
    }
}

贪心 代码实现：

import java.util.*;
public class Solution {
    /**
     * 
     * @param prices int整型一维数组 
     * @return int整型
     */
    public int maxProfit (int[] prices) {
        
        //记录最小值 初始值为数据范围最大+1
        int min = 10001;
        //记录最大值，初始值为0
        int max = 0;
        
        int n = prices.length;
        
            //遍历数组记录所遍历过的价格的最小值  
        for(int i = 0;i < n; i++){
            
            //每次使用当天的价格减去之前天数的最小价格 更新max
            max = Math.max(max,prices[i] - min);
            
            min = Math.min(min,prices[i]);
         
        }   
        return max;
        
    }
}

🚩二、买卖股票的最好时机(二)

原题传送门

🏳??🌈1.题目描述

假设你有一个数组prices，长度为n，其中prices[i]是某只股票在第i天的价格，请根据这个价格数组，返回买卖股票能获得的最大收益

1.你可以多次买卖该只股票，但是再次购买前必须卖出之前的股票

2. 如果不能获取收益，请返回0

3. 假设买入卖出均无手续费

数据范围： 1≤n≤1×10^5 ， 1≤ prices ≤10^4

要求：空间复杂度 O(n)，时间复杂度 O(n)

进阶：空间复杂度 O(1)，时间复杂度 O(n)

示例1

输入：

[8,9,2,5,4,7,1]

返回值：

7

说明：

在第1天(股票价格=8)买入，第2天(股票价格=9)卖出，获利9-8=1
在第3天(股票价格=2)买入，第4天(股票价格=5)卖出，获利5-2=3
在第5天(股票价格=4)买入，第6天(股票价格=7)卖出，获利7-4=3 总获利1+3+3=7，返回7

🏳??🌈2.题目分析

在第一题的基础上增加了可以多次买卖该只股票，那我们就不能用只买卖一次的思路思考，多次进行买卖然后求最大值，我们不能使用简单暴力法了，因为我们不知道总共需要进行多少次买卖。那我们就还使用动态规划模拟所有情况

思路1：动态规划

与第一题分析思路类似

dp[i][0] //表示第 i+1天没有持有股票  (i是从0开始)
dp[i][1] //表示第 i+1天持有股票  

推导状态转移方程：

• 对于dp[i][0] 可能有两种情况：

1. dp[i-1][0] 前一天没有持有股票，当天也不购买股票

2. dp[i-1][1] +prices[i] 前一天持有股票，当天卖出

dp[i][0] 就是 两种情况的最大值

• 对于dp[i][1] 有两种情况：

1. 可以多次买卖(注意和第一题的区别)，前一天没有持有股票，当天购买股票就是 dp[i-1][0]-prices[i]

2. 前一天持有股票，当天不进行任何操作 dp[i-1][1]

dp[i][1] 就是 两种情况的最大值

 //动态转移方程
dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1] + prices[i]);
            
 dp[i][1] = Math.max(dp[i-1][0]-prices[i],dp[i-1][1]);

结果是最后一天不持有股票的值 dp[n-1][0]

思路2：贪心（一次遍历）

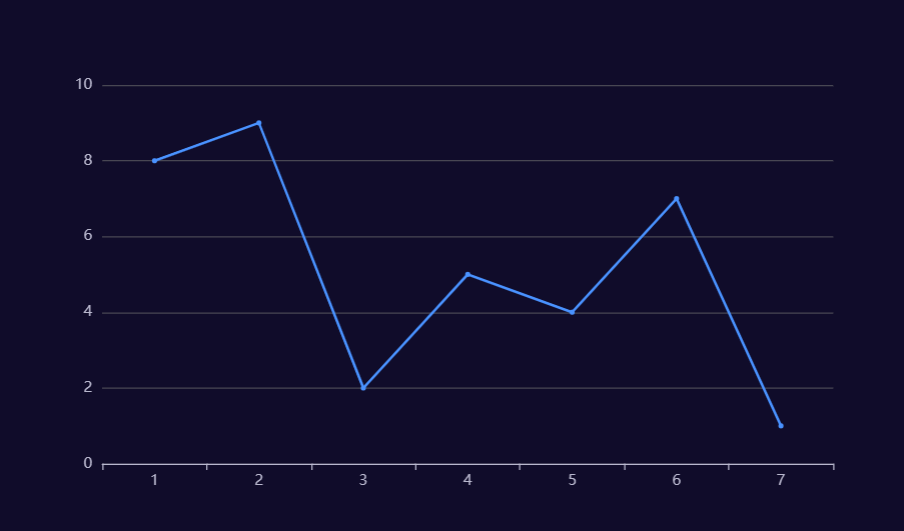
股票的变化是光滑的直线，由图可知每次买卖都是 极小值买入 极大值卖出，根据极小值极大值定义，极小值之后一定是递增的，那么在遇到极大值之前这之间的每个值 - 前面的值 就是最终 极大值 - 极小值（类似于差分，把一段上升直线的分成若干小段，每一小段增加的量累加到一起，就是整个上升直线的最大差值）

转化成编程思路 就是 如果 某一天比前一天股票的价格高，那么就进行买卖

    if(prices[i] > prices[i-1]){
       sum += prices[i] - prices[i-1];
         }

🏳??🌈3.代码实现

动态规划 代码实现：

import java.util.*;
public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * 计算最大收益
     * @param prices int整型一维数组 股票每一天的价格
     * @return int整型
     */
    public int maxProfit (int[] prices) {
          int n = prices.length;
        
        //下标i是从0开始
        //dp[i][0] 表示第i+1天不持有股票 从第一天到第i+1天的收益
        //dp[i][1] 表示第i+1天持有股票 从第一天到第i+1天的收益
      int[][] dp = new int[n][2];
        //初始化第一天不持有股票的收益0
        dp[0][0] = 0;
        //初始化第一天持有股票的收益 就是第一天买了当天的股票 -prices[0]
        dp[0][1] = -prices[0];
       
        //从第二天开始
        for(int i = 1;i < n; i++){
            
            dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1] + prices[i]);
            
            dp[i][1] = Math.max(dp[i-1][0]-prices[i],dp[i-1][1]);
        }
        
        //最后一天不持有股票此时的值就是最大收益
        return dp[n-1][0];
    }
}

贪心 代码实现：

import java.util.*;

public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * 计算最大收益
     * @param prices int整型一维数组 股票每一天的价格
     * @return int整型
     */
    public int maxProfit (int[] prices) {
          int n = prices.length;
        int sum = 0;
        
        for(int i = 1; i < n; i++){
            if(prices[i] > prices[i-1]){
                sum += prices[i] - prices[i-1];
            }
        }
     return sum;
    }
}

以上两道题目皆来源于牛客网，牛客网——程序员刷题、面试、找工作必备网站，超多大厂面试真题，面试高频题免费在线刷，直接对接大厂真题，专项专题训练，高效刷题、少走弯路。
👉牛客网👈

阅读世界，共赴山海

423全民读书节，邀你共读