图的拓扑排序
简介
AOV网
在一个表示工程(例如拍戏、教学安排)的有向图中,用顶点表示活动(每个阶段该做的事情),用弧表示活动之间的优先关系,这样的有向图为顶点表示活动的网叫做AOV网(Activity On vertex NetWord)。AOV网中的弧表示活动之间存在某种制约关系。并且AOV网中不能出现回路。
举个例子:拍戏这个工程,必须先把剧本给定好,然后再开始挑演员,选场地,进行拍摄,一步一步来,不能在拍摄过程中场地还没安排好就开始拍摄,也就是说拍摄的前提必须时场地给选好了。
拓扑序列
设G=(V,E)是一个具有n个顶点的有向图,V中的顶点序列V1,V2,V…满足若从顶点Vi到Vj有一条路径,则在顶点序列中顶点Vi比在顶点Vj之前。则经这样一个序列成为拓扑序列。
在任何有向无环图中,拓扑排序满足这样一种条件:对于有向图中任意两个顶点u和v,若存在一条有向边从u指向v,则在拓扑排序中u一定出现在v前面。
例如:
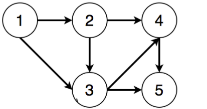
结点1必须在结点2、3之前
结点2必须在结点3、4之前
结点3必须在结点4、5之前
结点4必须在结点5之前
则一个满足条件的拓扑序列为[1, 2, 3, 4, 5]
而这样的序列可能不止一条。
拓扑排序
拓扑排序就是对一个有向图构造拓扑序列的过程。
拓扑排序的前提
必须是一个有向无环图(directed acyclic graph,DAG)
为什么说必须是有向无环图呢,看如下例子
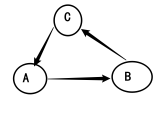
假设想从A开始,而根据拓扑排序原理,C在A的前面,那应该从C开始,而不是A,同样的B又排在C的前面,那也应该是从B开始而不是A或C…这样就分不清到底是从哪个点开始的,也就导致分不清顶点优先级。
基本思路
为了说明如何得到一个有向无环图的拓扑排序,我们首先需要了解有向图结点的入度(indegree)和出度(outdegree)的概念。
假设有向图中不存在环,也就是不存在起点和重点为统一结点的有向边。
入度: 设有向图中有一结点v,其入度即为当前所有从其他结点出发,终点为v的的边的数目。也就是所有指向v的有向边的数目。
出度: 设有向图中有一结点v,其出度即为当前所有起点为v,指向其他结点的边的数目。也就是所有由v发出的边的数目。
- 基本思路
(1)选择一个入度为0的顶点并输出
(2)从AOV网中删除此顶点及所有出边。
代码实现
- 链表实现
//拓扑排序
public ArrayList<String> topSort(){
//该数组存储各个顶点的入度值
int[] inDegree = new int[numOfVertex];
EdgeNode v;
//初始化所有入度值
for(VertexNode vertex : headVertex){
v = vertex.firstEdge;
while(v!=null){
inDegree[v.EdgeData]++;
v = v.nextEdge;
}
}
//定义一个队列,存储入度为0的结点数据值
Deque<String> deque = new ArrayDeque<>();
//定义一个集合,存储出栈的值
ArrayList<String> list = new ArrayList<>();
//将所有入度为0的结点入队
for(int i = 0; i<numOfVertex; i++){
if(inDegree[i] == 0){
deque.offer(headVertex[i].vertexData);
}
}
//当队列中存在元素时
while(!deque.isEmpty()){
//让最先入队的出队
String curr = deque.poll();
//出队后的元素用集合接收
list.add(curr);
//根据结点数据域获取入队为0的顶点的下标
int index = getIndexByString(curr);
//利用下标获取对应顶点
VertexNode vertex = headVertex[index];
EdgeNode e = vertex.firstEdge;
//遍历该顶点的邻接表
while(e != null){
int k = e.EdgeData;
//每次父节点弹出队列后,其直接子节点的入度减少
inDegree[k]--;
if(inDegree[k] == 0){
deque.offer(headVertex[k].vertexData);
}
e = e.nextEdge;
}
}
//如果list集合元素个数等于顶点个数,表示拓扑排序完成,没有环存在,反之不等于时表示图中存在环,则返回空集合
return list.size() == numOfVertex ? list : new ArrayList<>();
}
