1 栈

参考文章：
https://zhuanlan.zhihu.com/p/346164833
https://zhuanlan.zhihu.com/p/120965372#:~:text=%E6%A0%88%E6%98%AF%E4%B8%80%E7%A7%8D%20%E5%90%8E%E8%BF%9B%E5%85%88%E5%87%BA%EF%BC%88LIFO%EF%BC%89,%E7%9A%84%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%20%E8%BF%9B%E6%A0%88%E7%9A%84%E9%A1%BA%E5%BA%8F%E4%B8%BAa1%2Ca2%2Ca3%2Ca4%2Ca5%EF%BC%8C%E5%87%BA%E6%A0%88%E7%9A%84%E9%A1%BA%E5%BA%8F%E4%B8%BAa5%2Ca4%2Ca3%2Ca2%2Ca1

栈是一种特殊的线性表，仅允许在一端进行插入和删除。被允许插入和删除的一端为栈顶（top），另一端称为栈底（bottom），栈底是固定的，不允许进行插入和删除
在这里插入图片描述
栈的主要基本操作有：

InitStack(&S)：初始化栈
StackEmpty(S)：判断一个栈是否为空
Push(&S,x)：进栈，若栈未满，则将x加入到栈顶
pop(&S,&x)：出栈，若栈非空，则将栈顶元素出栈，并用x返回

栈的顺序存储

采用顺序存储的栈称为顺序栈，用数组实现。
栈的定义为：

#define STACK_SIZE 100

typedef int ElmType;

typedef struct{
    int top;    /* 栈顶指针 */
    ElmType data[STACK_SIZE];   /* 顺序栈 */
}SqStack;

栈顶指针：S.top，初始时设置S.top = -1；栈顶元素：S.data[top]；
进栈操作：先判断S.top==STACK_SIZE-1，若栈不满，S.top加1，然后将值送到栈顶。
出栈操作：栈非空时，先去栈顶元素值，然后再将栈顶指针减1
栈空条件：S.top==-1
栈满条件：S.top==STACK_SIZE-1
栈长：S.top+1

栈的链式存储

采用链式存储的栈称为链栈，链栈的优点是便于多个栈共享存储空间和提高其效率，且不存在栈满上溢的情况。通常采用单链表实现，并规定所有操作都是在单链表的表头进行的。这里规定链栈没有头结点，top指向栈顶元素，
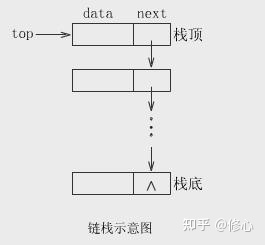
请添加图片描述
链栈的存储可定义为：

typedef int ElemType;
typedef struct LinkNode{
    ElemType data;
    struct LinkNode *next;
}LinkStack;

2 队列

队列是只允许在一端进程插入操作，在另一端进行删除操作的线性表。被允许插入的一端叫队尾（rear），被允许删除的一端叫队头（front）。

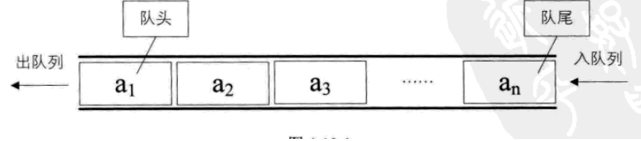
请添加图片描述
队列的主要基本操作有：

InitQueue(&Q)：初始化队列
QueueEmpty(Q)：判断队列是否为空
QueueLenght(Q)：判断队列中元素的个数
push(&Q,x)：入队，如果队列没有满，就在队尾插入x
pop(&Q,&x)：出队，如果队列非空，就在队首删除一个元素，并用x返回

队列的顺序存储

类型定义为：

#define QUEUE_SIZE 100
typedef int ElemType;
typedef struct 
{
    ElemType data[QUEUE_SIZE];  /* 队列 */
    int front;  /* 队首 */
    int rear;   /* 队尾 */
}SqQueue;

由于普通队列存在溢出问题，所以我们用循环队列，循环队列的定义和普通队列定义一样。
请添加图片描述

说明：这里浪费一个存储空间

初始化：rear=front=0
添加一个元素：如果队列没有满，则插入，即Q[rear] = x,rear= （rear+1）%QUEUE_SIZE
删除一个元素：如果队列非空，则删除，即*x=Q[front]，front = （front+1）% QUEUE_SIZE
判断队列是否为空：rear==front
判断队列是否满：(rear+1)%QUEUE_SIZE==front
队列元素个数：(rear-front+QUEUE_SIZE)%QUEUE_SIZE

队列的链式存储

队列的数组实现比较麻烦，需要考虑各种边界情况，所以通常使用链表形式来实现队列。

使用单向链表来实现链式队列，链式队列中存储front和rear即可。

typedef int ElemType;
typedef struct node
{
    int date;
    struct node *next;
}LinkNode;
typedef struct queue{
    LinkNode *front;
    LinkNode *rear;
}LinkQueue;

3 栈和队列的应用

用栈实现队列

参考文章：https://cloud.tencent.com/developer/article/1643318

LeedCode题目位置：232. 用栈实现队列

队列的特性是新加入的元素在队尾，最先入队的元素排在队首，按队首到队尾的顺序依次出栈。用栈实现队列，需要把新加入的元素保留在栈底，保证栈顶是队列最先加入的元素。

所以我们用两个栈A、B来实现，每次入队时，先把存放数据的栈A弹出到另一个栈B，然后把数据存到A，最后把B中的元素依次弹出压入A栈中，这样保证了新加入的元素在栈底。
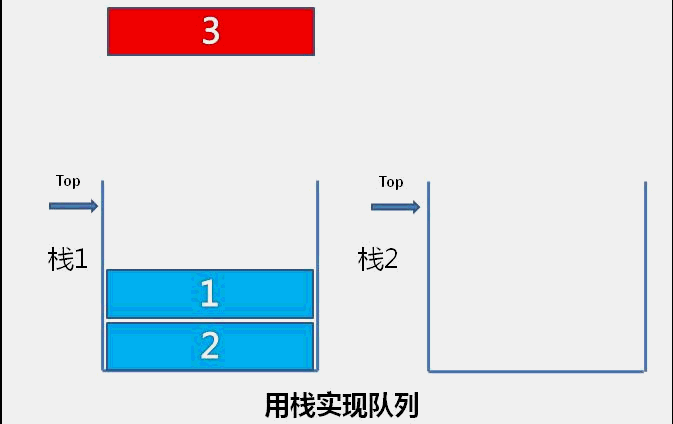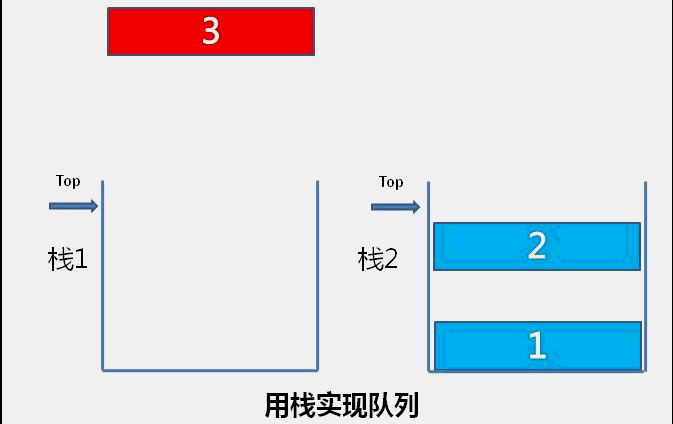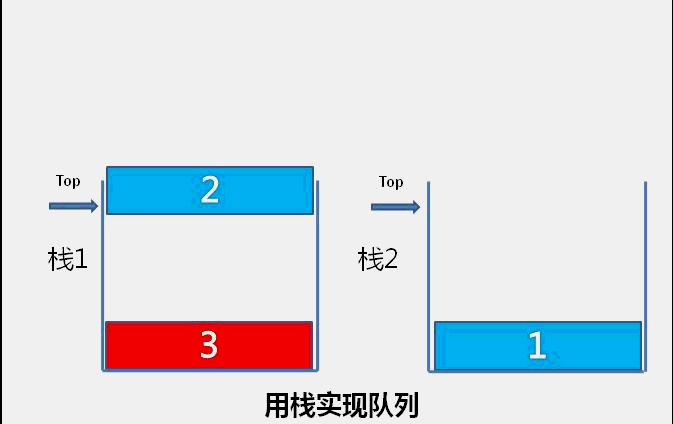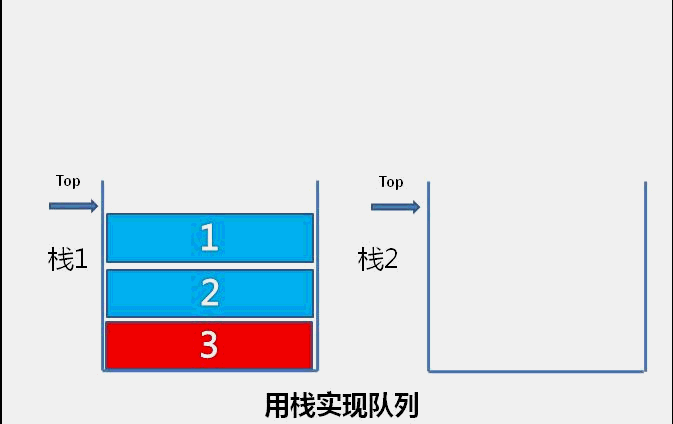
请添加图片描述
队列出队是把队列队首的删除，对应栈是把栈A的栈顶元素删除。

实现代码如下：

#include <stdlib.h>

typedef char bool;

#define SIZE 100
#define false 0
#define true 1
/* 栈的定义 */
typedef struct{
    int length;
    int data[SIZE];
}Stack;

/* 初始化栈 */
Stack *initStack()
{
    Stack * ret = malloc(sizeof(Stack));
    ret->length=-1;
    return ret;
}

/* 判断栈是否为空 */
bool StackEmpty(Stack *s)
{
    return s->length==-1;
}

/* 入栈操作 */
bool stackPush(Stack *s,int x)
{
    if(s->length==SIZE-1)
    {
        return false;
    }
    s->length++;
    s->data[s->length]=x;
    return true;
}
/* 出栈操作 */
bool stackPop(Stack *s,int *x)
{
    if(s->length==-1)
    {
        return false;
    }
    *x = s->data[s->length];
    s->length--;
    return true;
}

/* 释放栈 */
void freeStack(Stack *s)
{
    free(s);
}

typedef struct {
    Stack *inStack;
    Stack *outStack;
} MyQueue;

/* 创造队列 */
MyQueue* myQueueCreate() {
    MyQueue *ret = (MyQueue *)malloc(sizeof(MyQueue));
    ret->inStack = initStack();
    ret->outStack = initStack();
    return ret;
}

void myQueuePush(MyQueue* obj, int x) {
    int y;
    /* 先把栈A的元素依次弹出放到栈B */
    while(stackPop(obj->inStack,&y))
    {
        stackPush(obj->outStack,y);
    }
    /* 把入队的元素放到栈A的栈底 */
    stackPush(obj->inStack,x);
    /* 依次弹出栈B的元素放到栈A */
    while(stackPop(obj->outStack,&y))
    {
        stackPush(obj->inStack,y);
    }
}

int myQueuePop(MyQueue* obj) {
    int x;
    /* 删除栈A的栈顶元素 */
    stackPop(obj->inStack,&x);
    return x;
}

int myQueuePeek(MyQueue* obj) {
    return obj->inStack->data[obj->inStack->length];
}

bool myQueueEmpty(MyQueue* obj) {
    return StackEmpty(obj->inStack);
}

void myQueueFree(MyQueue* obj) {
    free(obj->inStack);
    free(obj->outStack);
    free(obj);
}

/**
 * Your MyQueue struct will be instantiated and called as such:
 * MyQueue* obj = myQueueCreate();
 * myQueuePush(obj, x);
 
 * int param_2 = myQueuePop(obj);
 
 * int param_3 = myQueuePeek(obj);
 
 * bool param_4 = myQueueEmpty(obj);
 
 * myQueueFree(obj);
*/

在这里插入图片描述

用队列实现栈

参考文章：https://cloud.tencent.com/developer/article/1643318
LeedCode题目位置：225. 用队列实现栈
栈的特性是新加入的元素出现在栈顶，删除的元素也在栈顶，队列的特性是新加入的特性在队尾，删除的元素在队首。
我们可以让数据先入队列，然后把队列的以前的数据依次出队再入队，这样保证了新压入的数据在队首，对应栈的栈顶。
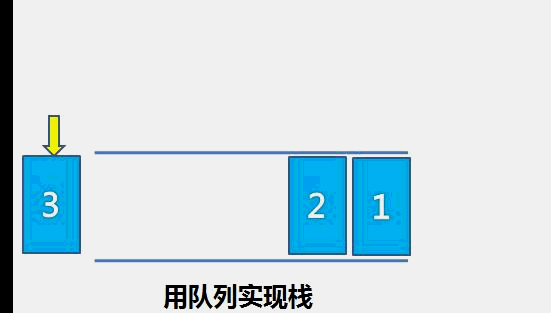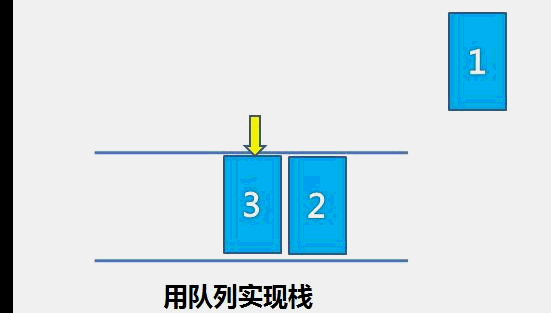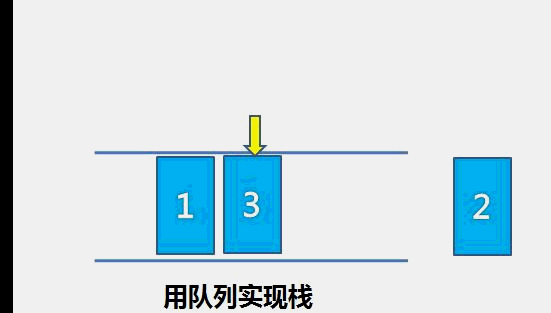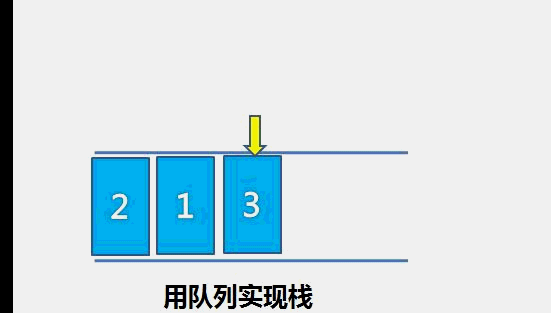
请添加图片描述
出栈的话，对应队列的操作就是把队首的元素删除即可。
实现代码如下：

#include <stdlib.h>

#define false 0
#define true 1
#define SIZE 101



typedef struct{
    int front;  // 队首
    int rear;   //队尾
    int data[SIZE];
}Queue;

/* 初始化队列 */
Queue * initQueue()
{
    Queue * ret = (Queue *)malloc(sizeof(Queue));
    ret->front=0;
    ret->rear=0;
    return ret;
}
/* 判断队列是否为空 */
bool QueueEmpty(Queue *q)
{
    if(q->front==q->rear)
    {
        return true;
    }else
        return false;
}

/* 入队 */
bool queuePush(Queue *q,int x)
{
    /* 队满 */
    if(q->front == (q->rear+1)%SIZE)
    {
        return false;
    }
    q->data[q->rear]=x;
    q->rear =(q->rear+1)%SIZE;
    return true;
}
/* 出队 */
bool QueuePop(Queue *q,int *x)
{
    /* 队列是否为空 */
    if(q->front==q->rear)
        return false;
    *x = q->data[q->front];
    q->front = (q->front+1)%SIZE;
    return true;
}
/* 获取队首元素 */
int getQueueTop(Queue *q)
{
    return q->data[q->front];
}
typedef struct {
    Queue *q;
} MyStack;


MyStack* myStackCreate() {
    MyStack *ret = (MyStack *)malloc(sizeof(MyStack));
    ret->q = initQueue();
    return ret;
}

void myStackPush(MyStack* obj, int x) {
    int y;
    /* 计算现在有多少个元素 */
    int length = (obj->q->rear-obj->q->front+SIZE)%SIZE;
    /* x入队 */
    queuePush(obj->q,x);
    for(int i=0;i<length;i++)
    {
        /* 出队 */
        QueuePop(obj->q,&y);
        /* 入队 */
        queuePush(obj->q,y);
    }
}
/* 只需将队首元素删除 */
int myStackPop(MyStack* obj) {
    int x;
    QueuePop(obj->q,&x);
    return x;
}

int myStackTop(MyStack* obj) {
    return getQueueTop(obj->q);
}

bool myStackEmpty(MyStack* obj) {
    return QueueEmpty(obj->q);
}

void myStackFree(MyStack* obj) {
    free(obj->q);
    free(obj);
}

/**
 * Your MyStack struct will be instantiated and called as such:
 * MyStack* obj = myStackCreate();
 * myStackPush(obj, x);
 
 * int param_2 = myStackPop(obj);
 
 * int param_3 = myStackTop(obj);
 
 * bool param_4 = myStackEmpty(obj);
 
 * myStackFree(obj);
*/

在这里插入图片描述

最小栈

LeedCode位置：155. 最小栈
题目要求在常数时间内检索到最小元素的栈，所以我们在栈里面设置一个变量min来记录最小元素的位置。

当插入元素，如果插入的元素比栈内的元素都要小，这个时候需要更新min；当删除元素时，如果此时最小的元素在栈顶，也需要更新min值。

代码实现如下：

#include <stdlib.h>

#define SIZE 30000

typedef struct {
    int length;    //记录元素个数,始终指向栈顶元素
    int min;    //记录最小元素的位置
    int data[SIZE];
} MinStack;

int getStackMin(MinStack *s)
{
    int min =0;
    for(int i=1;i<=s->length;i++)
    {
        if(s->data[min]>s->data[i])
        {
            min = i;
        }
    }
    return min;
}

MinStack* minStackCreate() {
    MinStack *ret = (MinStack *)malloc(sizeof(MinStack));
    ret->length = -1;
    ret->min = 0;
    return ret;
}

void minStackPush(MinStack* obj, int val) {
    obj->data[++obj->length]=val;
    /* 插入的元素比栈内的元素都要小，这个时候需要更新min */
    if(val<obj->data[obj->min])
        obj->min = obj->length;
}

void minStackPop(MinStack* obj) {
    obj->length--;
    /* 删除元素时，如果此时最小的元素在栈顶，也需要更新min值 */
    if(obj->min==(obj->length+1))
    {
        obj->min = getStackMin(obj);
    }
}

int minStackTop(MinStack* obj) {
    return obj->data[obj->length];
}

int minStackGetMin(MinStack* obj) {
    return obj->data[obj->min];
}

void minStackFree(MinStack* obj) {
    free(obj);
}

/**
 * Your MinStack struct will be instantiated and called as such:
 * MinStack* obj = minStackCreate();
 * minStackPush(obj, val);
 
 * minStackPop(obj);
 
 * int param_3 = minStackTop(obj);
 
 * int param_4 = minStackGetMin(obj);
 
 * minStackFree(obj);
*/