[数据结构与算法]C. Make it Increasing

https://codeforces.com/contest/1668/problem/C

input

5
1 2 3 4 5

output

4

input

7
1 2 1 2 1 2 1

output

10

input

8
1 8 2 7 3 6 4 5

output

16

题意

给定 $n$ 以及 n 个数表示为 $a_i$ ，现你需要通过最小操作数将 $b$ 数组变成严格递增的数组，其中 $b$ 数组内元素一开始都是 0 ，每次操作中，对于 $b_i$ 可以 变成 $b_i+a_i$ $or$ $b_i?a_i$
注：$n$ 为 $5e3$

思路
对于一开始都相等的序列，选定某个特殊点，则其左边都减小，右边都增大

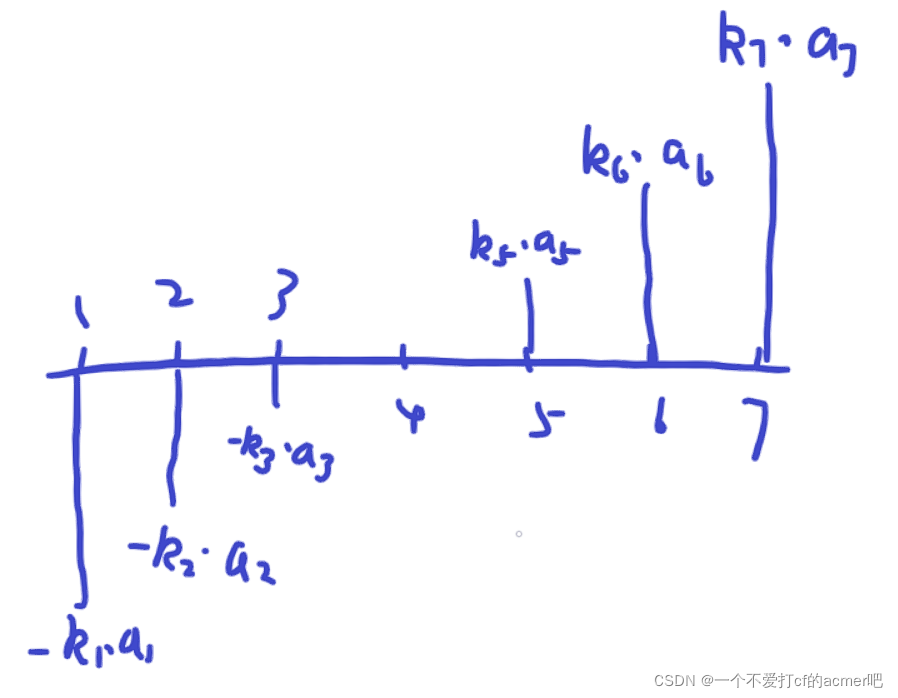
我们可以想一下，最终构造的方法是不是特殊点一定是是 $0$ ，即不用动
（如下图）（并不严格的证明）
假设一下 $b_5$ 先 $+a_5$
对于 $b_{6?10}$ 都需要使用至少 1 次步数来平衡，如果其中 $a_{6?10}$某一个小于$a_5$则需要两步或更多等 ，而换来的只是$b_4$ 不用动，而$b_{1?3}$ 仍需正常的偏移构造递增序列，实际上非常亏

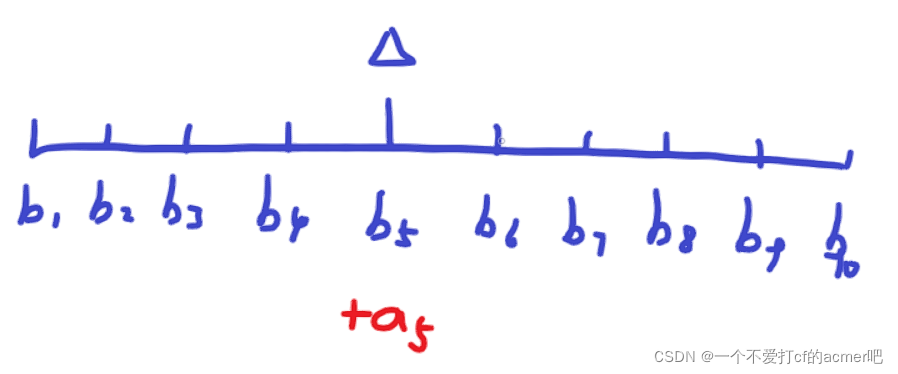
综上，我们只需要枚举 $1?n$ 作为特殊点，然后计算对应的步数去最小即可

AC代码

#include <bits/stdc++.h>
#define endl '\n'
#define AC return 0;
using namespace std;
//#define ll long long
#define int long long

int e[5005];
int b[5005];
void slove()
{
    int n;
    cin >> n;
    for(int i = 1; i <= n; i++)
        cin >> e[i];
    int ans = 1e18;
    for(int pos = 1; pos <= n; pos++)
    {
        int res = 0;
        for(int i = 1; i <= n; i++)
            b[i] = 0;
        // cout << pos << endl;
        //left
        for(int i = pos - 1; i >= 1; i--)
        {
            int c = b[i + 1] - b[i];
            int k = (c + e[i]) / e[i];
            // cout << k << endl;
            b[i] = k * e[i];
            res += k;
        }

        //rig
        for(int i = pos + 1; i <= n; i++)
        {
            int c = b[i - 1] - b[i];
            int k = (c + e[i]) / e[i];
            b[i] = k * e[i];
            res += k;
        }
        // for(int i = 1; i <= n; i++)
        //     cout << b[i] << " " ;
        // cout << endl;
        ans = min(ans,res);
    }    
    cout << ans << endl;
    
    
}

signed main()
{
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    //int T;cin >> T; while(T--)
    slove();
    AC
}

发现我的题解都好多画图（

阅读世界，共赴山海

423全民读书节，邀你共读