[数据结构与算法] 算法：选择排序及优化

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 算法：选择排序及优化 -> 正文阅读

[数据结构与算法]算法：选择排序及优化

前言

如果想深入了解的话建议先看看算法概述

为了方便用来测试的数组一成不变，我们可以来一个随机数组

const arr = []
const arrLength = 11 //可以随机长度 Math.floor(Math.random() * 30) + 1
for (let i = 0; i < arrLength; i++) {
    arr.push(Math.floor(Math.random() * 99) + 1)
}
console.log(arr, 'arr')

算法描述

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

动图演示

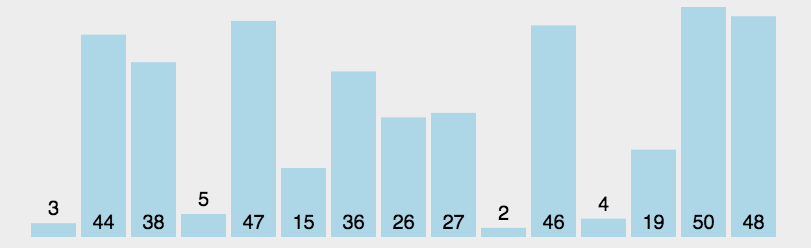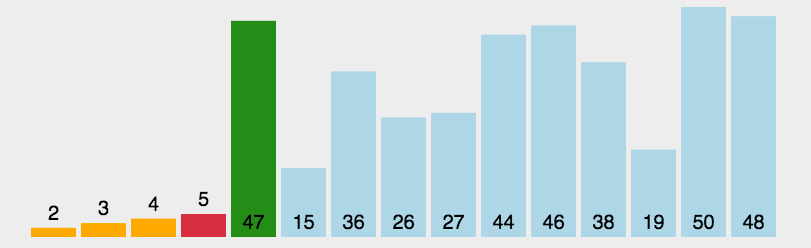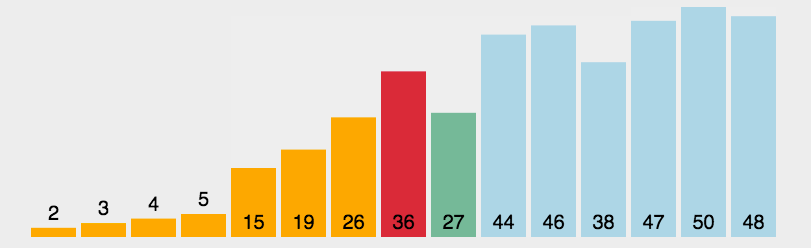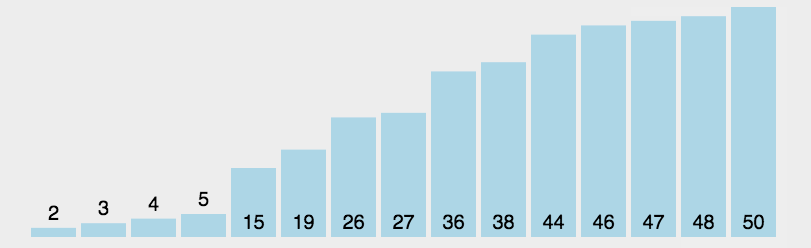
在这里插入图片描述

代码实现

// 选择
function selectionSort(arr){
    const len = arr.length
    for(let i=0;i<len-1;i++){
        let min = i
        for(let j=i+1;j<len;j++){
            if(arr[j]<arr[min]){
                min = j
            }
        }
        const tem = arr[i]
        arr[i] = arr[min]
        arr[min] = tem
    }
    return arr
}
console.log(selectionSort(arr),'selectionSort arr')

优化思考

上面的代码对比次数是固定的，如果还记得高中数学中的排列组合的话会发现次数 count 和数组长度 length 的关系：

count = (length-1)*length/2

那么上面要怎么优化呢？

试想，上述方案中的主要思路是，每次遍历剩余元素，找出其中最小值，只排定最小值。
我们这样，每次遍历剩余元素的时候，找出其中最小值和最大值，并排定最小值和最大值。
因为有可能数组第一个元素是最大值，所以数组的头尾元素也要参与遍历。

function selectionSort(arr) {
  const len = arr.length
  let count = 0
  for (let left = 0,right=len-1; left < right; left++,right--) {
    let min = left
    let max = right
    for (let j = left; j <= right; j++) {
      count++
      if (arr[j] < arr[min]) {
        min = j
      }
      if (arr[j] > arr[max]) {
        max = j
      }
    }
    if(left !== min){
      const tem = arr[left]
      arr[left] = arr[min]
      arr[min] = tem
    }
    if(max===left){// 此处是先排最小值的位置，所以得考虑最大值在最小位置的情况
      max=min
    }
    if(right !== max){
      const tem = arr[right]
      arr[right] = arr[max]
      arr[max] = tem
    }
  }
  console.log(count, 'selectionSort count')
  return arr
}