[数据结构与算法]【数学建模】—— 层次分析法（AHP）

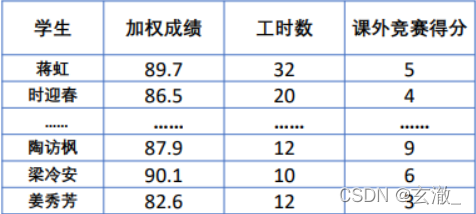
层次分析法

The analytic hierarchy process (AHP)
建模比赛中最基础的算法之一，主要用于解决评价类的

解决评价类问题，首先要想到以下三个问题：

1. 我们评价的目标是什么？
2. 我们为了达到这个目标有哪几种可以选择的方案？
3. 评价的标准或者是指标是什么？（我们根据什么东西来评价好坏）

判断矩阵

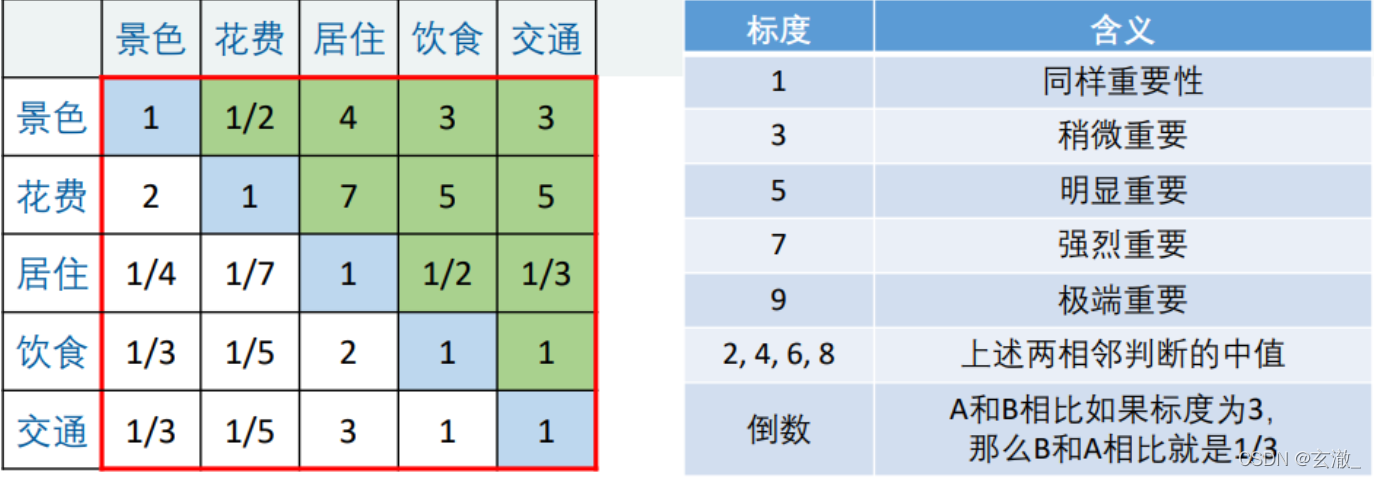
总结：上面这是一个 5 × 5 的矩阵，我们记为 A， 对应的元素为 $a_{ij}$

1. $a_{ij}$表示的意义是，与指标 j 相比， i 的重要程度
2. 当 i = j 时，两个指标相同，因此同等重要记为 1，这就解释了主对角元素为 1
3. $a_{ij}$ > 0 且满足 $a_{ij}$ × $a_{ji}$ = 1(我们称满足这一条件的矩阵为正互反矩阵)

实际上，上面这个矩阵就是层次分析法中的**判断矩阵**

一致矩阵

矩阵中每个元素$a_{ij}$ > 0且满足$a_{ij}$ × $a_{ji}$ = 1 ，则我们称该矩阵为正互反矩阵。

在层次分析法中，我们构造的判断矩阵均是正互反矩阵。

若正互反矩阵满足$a_{ij}$ × $a_{jk}$ = $a_{ik}$，则我们称其为一致矩阵。

一致性检验

引理：A为n阶方阵，且r(A) = 1,则A有一个特征值tr(A),其余特征值为0

因此，一致矩阵的各行成比例，所以一致矩阵的特征值为1

由引理可知：一致矩阵有一个特征值为n，其余特征值均为0

若正互反矩阵（判断矩阵）满足$a_{ij}$ × $a_{jk}$ = $a_{ik}$，则我们称其为一致矩阵

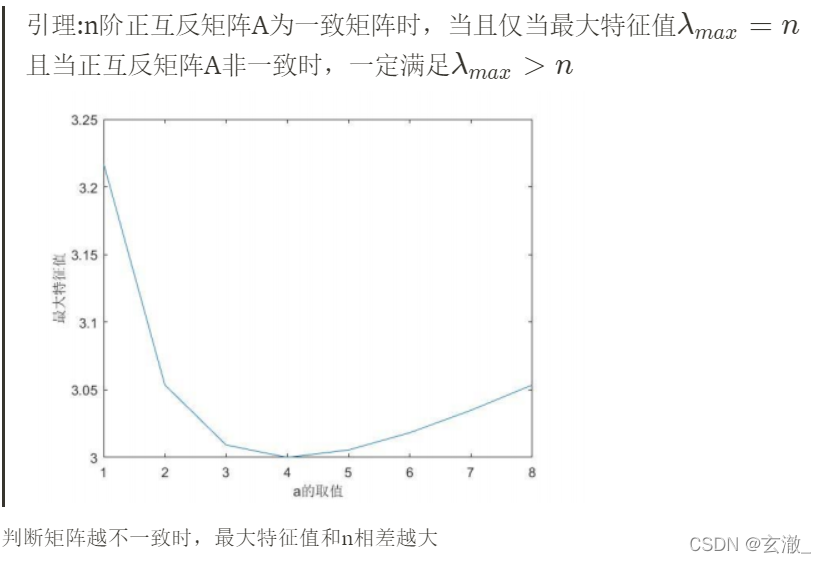
引理:n阶正互反矩阵A为一致矩阵时，当且仅当最大特征值${\lambda }_{max}=n$
且当正互反矩阵A非一致时，一定满足${\lambda }_{max}>n$

判断矩阵越不一致时，最大特征值和n相差越大

一致性检验的步骤

第一步：计算一致性指标CI

$CI=\frac{{\lambda }_{max}?n}{n?1}$

第二步：查找对应的平均随机一致性指标RI

第三步：计算一致性比例CR

$CR=\frac{CI}{RI}$

如果 CR < 0.1 ,则可认为判断矩阵的一致性可以接受；否则需要对矩阵进行修正

方法1：算术平均法求权重

第一步：将判断矩阵按照列归一化（每一个元素除以其所在的列）

第二步：将归一化的各列相加（按行求和）

第三步：将相加后得到的向量中每一个元素除以n即可得到权重向量

几何平均法求权重

第一步：将A的元素按照行相乘得到一个新的列向量

第二步：将新的向量的每个分量开n次方

第三步：对该列向量进一步归一化即可得到权重向量

层次分析法

层次分析法（The Analytic Hierarchy Process即 AHP)是由美国运筹学家、 匹兹堡大学教授T . L. Saaty于20世纪70年代创立的一种系统分析与决策的综合 评价方法，是在充分研究了人类思维过程的基础上提出来的，它较合理地解 决了定性问题定量化的处理过程。

AHP的主要特点是通过建立递阶层次结构，把人类的判断转化到若干因 素两两之间重要度的比较上，从而把难于量化的定性判断转化为可操作的重 要度的比较上面。在许多情况下，决策者可以直接使用AHP进行决策，极大 地提高了决策的有效性、可靠性和可行性，但其本质是一种思维方式，它把 复杂问题分解成多个组成因素，又将这些因素按支配关系分别形成递阶层次 结构，通过两两比较的方法确定决策方案相对重要度的总排序。整个过程体 现了人类决策思维的基本特征，即分解、判断、综合，克服了其他方法回避 决策者主观判断的

决评价类问题，大家首先要想到以下三个问题：
①我们评价的目标是什么
②我们为了达到这个目标有哪几种可选的方案？
③价的准则或者说指标是什么？（我们根据什么东西来评价好坏）

层次分析法第一步

分析系统中各因素之间的关系，建立系统的递阶层次结构.

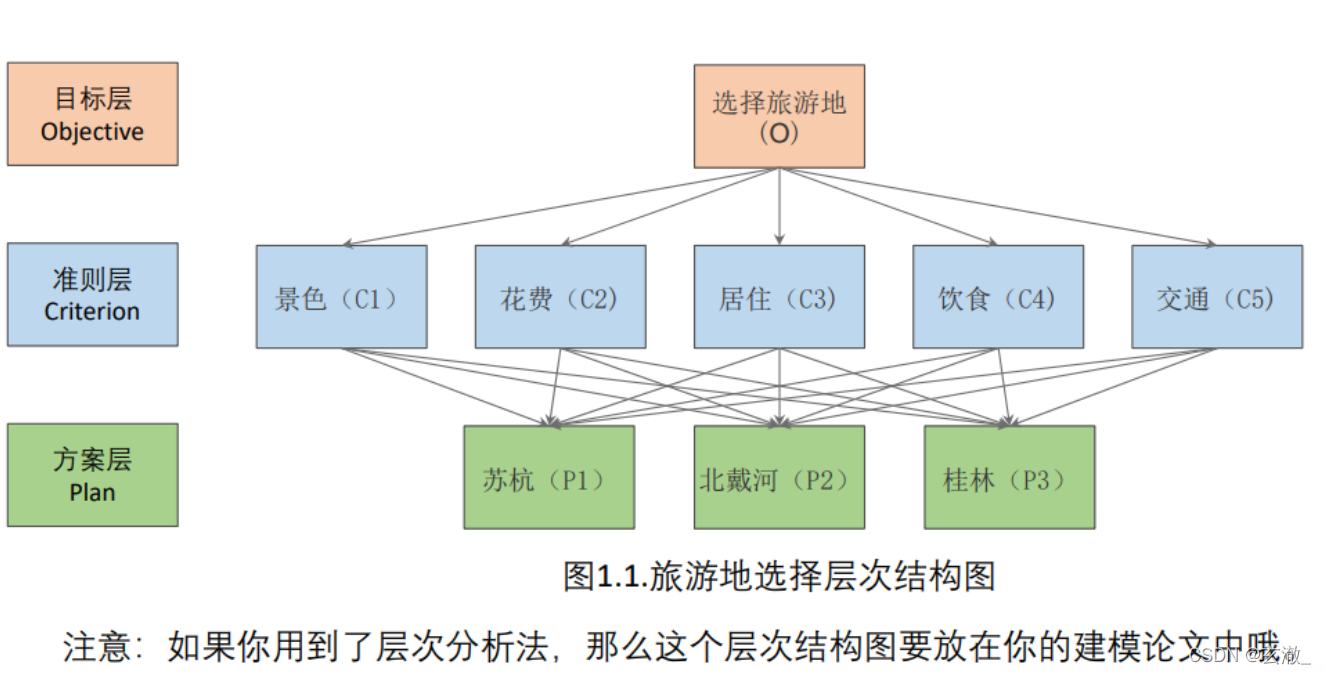
层次分析法第二步

对于同一层次的各元素关于上一层次中某一准则的重要 性进行两两比较，构造两两比较矩阵（判断矩阵）

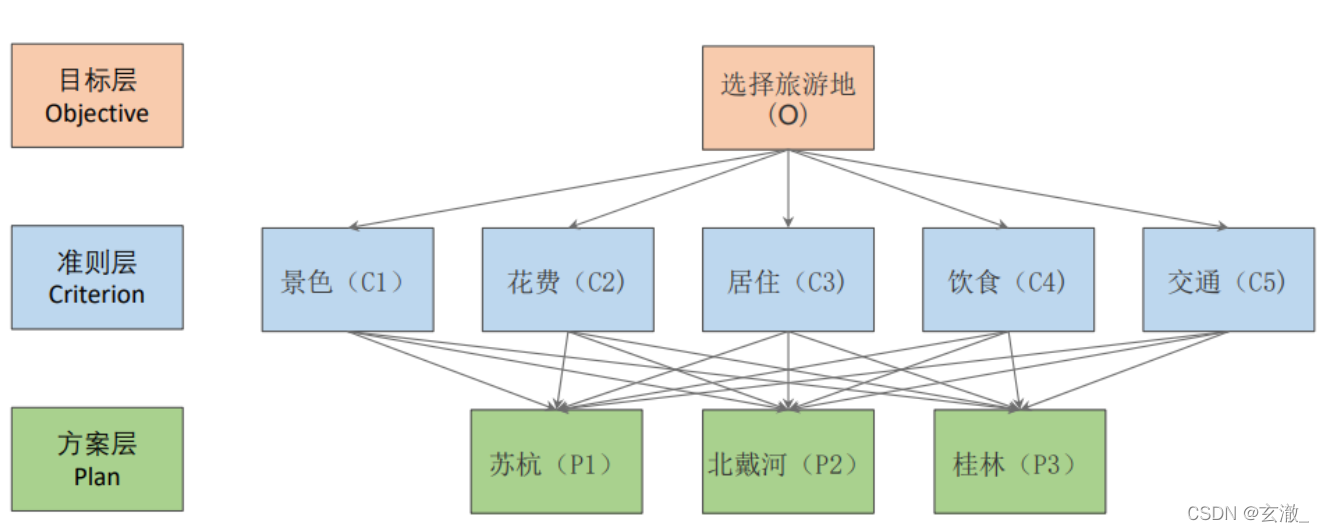
构造判断矩阵

层次分析法第三步

由判断矩阵计算被比较元素对于该准则的相对权重， 并进行一致性检验（检验通过权重才能用）。

三种方法计算权重

1. 算术平均法
2. 几何平均法
3. 特征值法

强烈建议大家在比赛时三种方法都使用

以往的论文利用层次分析法解决实际问题时，都是采用其中某一种方法 求权重，而不同的计算方法可能会导致结果有所偏差。为了保证结果的 稳健性，本文采用了三种方法分别求出了权重后计算平均值，再根据得 到的权重矩阵计算各方案的得分，并进行排序和综合分析，这样避免了 采用单一方法所产生的偏差，得出的结论将更全面、更有效

注：（1）一致矩阵不需要进行一致性检验，只有非一致矩阵的判断矩阵才需要进 行一致性检验；（2）在论文写作中，应该先进行一致性检验，通过检验后再计算 权重，视频中讲解的只是为了顺应计算过程。

层次分析法第四步

根据权重矩阵计算得分，并进行排序。

层次分析法的一些局限性

(1)评价的决策层不能太多，太多的话n会很大，判断矩阵和一致矩阵差异 可能会很大。

(2)如果决策层中指标的数据是已知的，那么我们如何利用这些数据来使得 评价的更加准确呢？

阅读世界，共赴山海

423全民读书节，邀你共读