[数据结构与算法]【玩转九大排序①】插入排序 + 希尔排序（思想与算法实现）

一、插入排序基本介绍

①基本思想

?插入排序的核心思想是：维护一个有序的区间。举个生活的例子，我们如何将一副凌乱的扑克牌从大到小有序排列呢？假设我们已经有一个有序区间 [3, 5, 6]，现有一张大小为4的牌，显然我们应该插入到[3, 5]之间，但是计算机不能像人脑一样一看就知道，所以需要从大到小与我们手上已经有序的牌一一比较，进而得到我们应当插入的位置。

②代码呈现

void Insertsort(int* arr, int sz)
{
	for (int i = 1; i < sz; i++)  // (1)
	{
		int end = i;
		int tmp = arr[i];
		while (end)
		{
			if (tmp < arr[end - 1]) 
			{
				arr[end] = arr[end - 1]; //(2)
				end--;
			}
			else
				break;
		}
		arr[end] = tmp;  //(3)
	}
}

【代码细节剖析】

1. 从i = 0时相当于只有一张牌，自然就是有序的，所以就从 i = 1开始遍历，即从第二张牌开始进行比较插入的过程
2. arr[end] < arr[end - 1]，所以end的位置应该由end - 1的数来占。往后覆盖后留出新的位置 end - 1。继续往后比较，知道找到应当插入的位置。
3. 跳出循环的时候，即tmp > arr[end - 1]，所以不用再往前比，end位置就是tmp要插入的位置。

【时间复杂度分析】
最坏情况为原序列逆序，时间复杂度为 O(N^2)。

【10万数据量测试用时单位（ms）】

③错误代码辨析

void Insertsort(int* arr, int sz)
{
	for (int i = 1; i < sz; i++) 
	{
		int end = i;
		int tmp = arr[i];
		while (end)
		{
			if (tmp < arr[end - 1])
			{
				arr[end] = arr[end - 1];
				end--;
			}
			else
			{
				arr[end] = tmp;
				break;
			}
		}
	}
}

Q：可以将arr[end]的赋值放在while循环里面吗？
?不可以。看下面的有序数列【1， 2， 3】，插入数字0，显然我们要插在头部，但此时end = 0，循环结束，我们也就没有机会插入了。

二、希尔排序基本介绍

①基本思想

?希尔排序的基本思想仍然是插入排序的思想，但是通过一些方式来加快排序的速度。我们先来看这样一组序列 【6， 5， 4， 3， 2， 1】，显然在每一次插入的时候待插入的数据都要比较到头才截止，这可是致命的，如果待排序的数量级比较大，排序的速度就会很慢。所以，我们能不能尽可能的让大的数据更快的往后移动， 小的数据更快的往前移动呢？这就是希尔排序核心的问题。
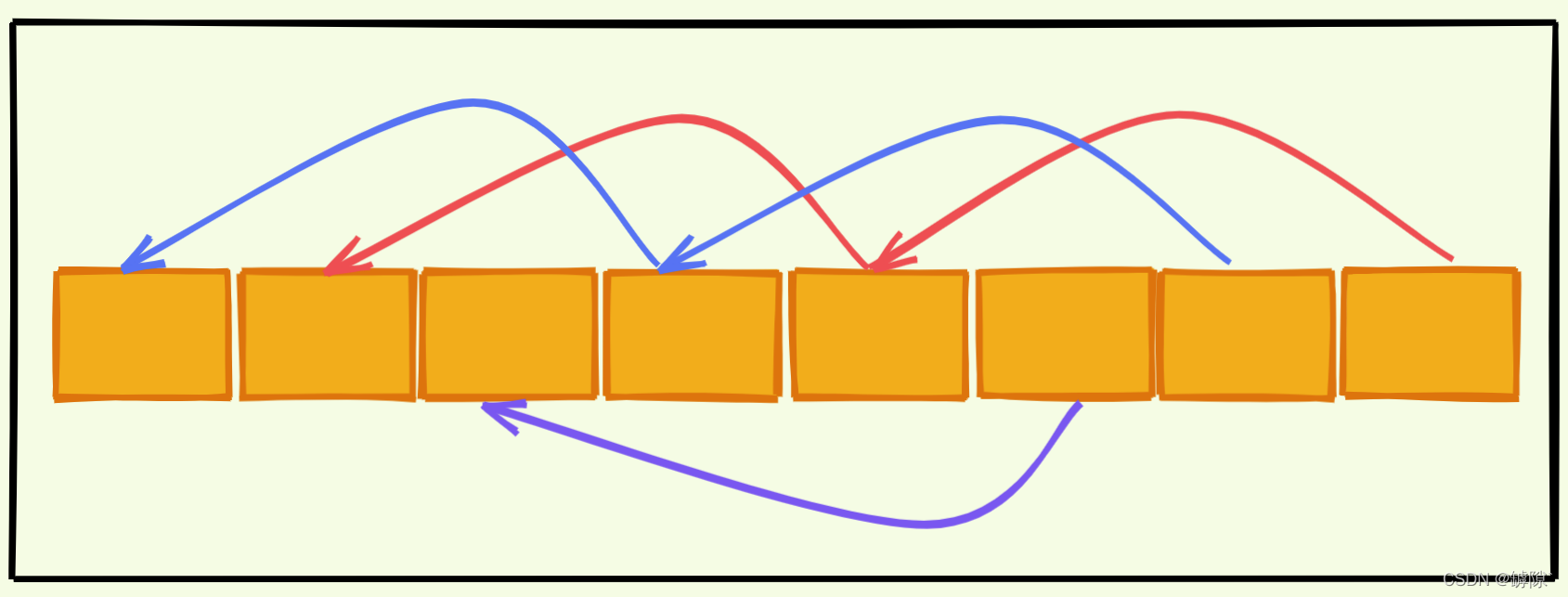
?为了实现更快速的移动，我们不再是相邻的数据之间进行比较，而是隔位比较，当然交换也是隔位交换。

显然我们可以得出以下的关系（记间隔大小为gap）：

• gap越大，数据移动越快
• gap越小， 数据更接近有序

?所以在插入排序的基础之上，我们只需增加 预排序" 的过程即可。即先进行有gap的预排序，使得大数尽快往后移动，小数尽快往前移动，最后再来一次gap为1的排序，实现数组的最终有序即可。
?你可能会有疑问，这样希尔排序的次数更多了，排序时间不会更长吗。我们最后拿测试数据说话。

②代码呈现

void Shellsort(int* arr, int sz)
{
	int gap = sz;
	while (gap > 1)
	{
		gap = gap / 3 + 1;             //(1)
		for (int i = gap; i < sz; i++) //(2)
		{
			int end = i;
			int tmp = arr[end];
			while (end >= gap)         //(3)
			{
				if (tmp < arr[end - gap])
				{
					arr[end] = arr[end - gap];
					end -= gap;
				}
				else
					break;
			}
			arr[end] = tmp;
		}
	}
}

【代码细节剖析】

1. +1保证了gap = 1的情况一定会出现。gap > 1时进行预排序，gap = 1时进行标准的插入排序。我们就此巧妙的统一了预排序和标准排序的代码。
2. 这里 i 的增长方式是+1，而不是加gap， 也就不必要写成双重循环了。
3. 注意别写成while(end)了，这样会存在越界的风险。

【时间复杂度分析】
希尔排序的时间复杂度是最难算的，这里就不做数学推导：
平均时间复杂度：O(Nlog2N)
时间复杂度范围：（O(N^1.3) ~ O(N^2)）

【10万数据量测试时间（单位ms）】
?从上面的数据我们可以看出，虽然希尔排序进行了多次的预排序，但是正是这些预排序使得原数据更加趋近于有序，从而极大的加快了排序的速度。

阅读世界，共赴山海

423全民读书节，邀你共读