二叉树的遍历
- 前(根)序遍历:先输出父节点,再遍历左子树和右子树
- 中(根)序遍历:先输出左子树,再输出父节点,在输出右子树
- 后(根)序遍历:先输出左子树,在输出右子树,最后输出父结点
- 三种遍历方式的区别在于根节点的输出时机
代码实现
/***
* 二叉树
* @author laowa
*
*/
class BinaryTree{
/**
* 根节点
*/
Node root;
public BinaryTree(Node root) {
this.root = root;
}
/**
* 先序遍历
*/
public void preOrder() {
if(this.root==null) {
System.out.println("二叉树为空");
}
this.root.preOrder();
}
/**
* 中序遍历
*/
public void infixOrder() {
if(this.root==null) {
System.out.println("二叉树为空");
}
this.root.infixOrder();
}
/**
* 后序遍历
*/
public void postOrder() {
if(this.root==null) {
System.out.println("二叉树为空");
}
this.root.postOrder();
}
}
/**
* 树的节点
* @author laowa
*
*/
class Node{
int no;
String name;
/**
* 左子节点
*/
Node left;
/**
* 右子节点
*/
Node right;
public Node(int no,String name) {
this.no = no;
this.name = name;
}
@Override
public String toString() {
return "[no="+no+"\tname="+name+"]";
}
/**
* 先序遍历
*/
public void preOrder() {
//1.打印当前节点
System.out.println(this);
//2.如果左子树不为空,则向左递归遍历
if(this.left!=null) {
this.left.preOrder();
}
//3.如果有子树不为空,则向右递归遍历
if(this.right!=null) {
this.right.preOrder();
}
}
/**
* 中序遍历
*/
public void infixOrder() {
//1.如果左子树不为空,则向左递归遍历
if(this.left!=null) {
this.left.infixOrder();
}
//2.打印当前节点
System.out.println(this);
//3.如果右子树不为空,则向右递归遍历
if(this.right!=null) {
this.right.infixOrder();
}
}
/**
* 后序遍历
*/
public void postOrder() {
//1.如果左子树不为空,则向左递归遍历
if(this.left!=null) {
this.left.postOrder();
}
//2.如果右子树不为空,则向右递归遍历
if(this.right!=null) {
this.right.postOrder();
}
//3.打印当前节点
System.out.println(this);
}
}
二叉树的查找
二叉树的查找和遍历一样,也分前、中、后序查找;根据比对树中节点的顺序来区分
代码实现
/***
* 二叉树
*
* @author laowa
*
*/
class BinaryTree {
/**
* 根节点
*/
Node root;
public BinaryTree(Node root) {
this.root = root;
}
/**
* 先序遍历
*/
public void preOrder() {
if (this.root == null) {
System.out.println("二叉树为空");
}
this.root.preOrder();
}
/**
* 中序遍历
*/
public void infixOrder() {
if (this.root == null) {
System.out.println("二叉树为空");
}
this.root.infixOrder();
}
/**
* 后序遍历
*/
public void postOrder() {
if (this.root == null) {
System.out.println("二叉树为空");
}
this.root.postOrder();
}
/**
* 前序查找
* @param no 目标节点编号
* @return 目标节点
*/
public Node preSearch(int no) {
Node helper = this.root.preSearch(no);
if(helper==null) {
throw new RuntimeException("没有找到目标节点");
}
return helper;
}
/**
* 中序查找
* @param no 目标节点编号
* @return 目标节点
*/
public Node infixSearch(int no) {
Node helper = this.root.infixSearch(no);
if(helper==null) {
throw new RuntimeException("没有找到目标节点");
}
return helper;
}
/**
* 后序查找
* @param no 目标节点编号
* @return 目标节点
*/
public Node postSearch(int no) {
Node helper = this.root.postSearch(no);
if(helper==null) {
throw new RuntimeException("没有找到目标节点");
}
return helper;
}
}
/**
* 树的节点
*
* @author laowa
*
*/
class Node {
int no;
String name;
/**
* 左子节点
*/
Node left;
/**
* 右子节点
*/
Node right;
public Node(int no, String name) {
this.no = no;
this.name = name;
}
@Override
public String toString() {
return "[no=" + no + "\tname=" + name + "]";
}
/**
* 先序遍历
*/
public void preOrder() {
// 1.打印当前节点
System.out.println(this);
// 2.如果左子树不为空,则向左递归遍历
if (this.left != null) {
this.left.preOrder();
}
// 3.如果有子树不为空,则向右递归遍历
if (this.right != null) {
this.right.preOrder();
}
}
/**
* 中序遍历
*/
public void infixOrder() {
// 1.如果左子树不为空,则向左递归遍历
if (this.left != null) {
this.left.infixOrder();
}
// 2.打印当前节点
System.out.println(this);
// 3.如果右子树不为空,则向右递归遍历
if (this.right != null) {
this.right.infixOrder();
}
}
/**
* 后序遍历
*/
public void postOrder() {
// 1.如果左子树不为空,则向左递归遍历
if (this.left != null) {
this.left.postOrder();
}
// 2.如果右子树不为空,则向右递归遍历
if (this.right != null) {
this.right.postOrder();
}
// 3.打印当前节点
System.out.println(this);
}
/**
* 前序查找
*
* @param no
* 目标节点的编号
* @return 目标节点
*/
public Node preSearch(int no) {
// 辅助节点,存储找到的目标节点
Node helper = null;
// 1.判断当前节点是否是目标节点
if (this.no == no) {
helper = this;
}
// 2.如果左子树不为空,且目标节点还没有找到,则向左子树递归查找
if (this.left != null && helper == null) {
helper = this.left.preSearch(no);
}
// 3.如果右子树不为空,且目标节点还没有找到,则向右子树递归查找
if (right != null && helper == null) {
helper = this.right.preSearch(no);
}
// 返回最终结果
return helper;
}
/**
* 中序查找
*
* @param no
* 目标节点的编号
* @return 目标节点
*/
public Node infixSearch(int no) {
// 辅助节点,存储找到的目标节点
Node helper = null;
// 1.如果左子节点不为空,则向左递归查找
if (this.left != null) {
helper = this.left.infixSearch(no);
}
// 2.如果左子树没找到目标节点,判断当前是否是目标节点
if (helper == null && this.no == no) {
helper = this;
}
// 3.如果左子树和当前当前节点都没有找到,则向右递归查找
if (helper == null && this.right != null) {
helper = this.right.infixSearch(no);
}
return helper;
}
/**
* 后序查找
*
* @param no
* 目标节点的编号
* @return 目标节点
*/
public Node postSearch(int no) {
// 辅助节点,存储找到的目标节点
Node helper = null;
// 1.如果左子节点不为空,则向左递归查找
if (this.left != null) {
helper = this.left.postSearch(no);
}
// 3.如果左子树和当前当前节点都没有找到,则向右递归查找
if (helper == null && this.right != null) {
helper = this.right.postSearch(no);
}
// 2.如果左子树没找到目标节点,判断当前是否是目标节点
if (helper == null && this.no == no) {
helper = this;
}
return helper;
}
}
二叉树的简单删除
- 如果删除的是叶子节点,将该叶子节点的父节点的指针置空
- 如果删除的是非叶子节点,删除该节点为根节点的整颗子树
代码实现
/***
* 二叉树
*
* @author laowa
*
*/
class BinaryTree {
/**
* 根节点
*/
Node root;
public BinaryTree(Node root) {
this.root = root;
}
/**
* 先序遍历
*/
public void preOrder() {
if (this.root == null) {
System.out.println("二叉树为空");
return;
}
this.root.preOrder();
}
/**
* 中序遍历
*/
public void infixOrder() {
if (this.root == null) {
System.out.println("二叉树为空");
return;
}
this.root.infixOrder();
}
/**
* 后序遍历
*/
public void postOrder() {
if (this.root == null) {
System.out.println("二叉树为空");
return;
}
this.root.postOrder();
}
/**
* 前序查找
* @param no 目标节点编号
* @return 目标节点
*/
public Node preSearch(int no) {
Node helper = this.root.preSearch(no);
if(helper==null) {
throw new RuntimeException("没有找到目标节点");
}
return helper;
}
/**
* 中序查找
* @param no 目标节点编号
* @return 目标节点
*/
public Node infixSearch(int no) {
Node helper = this.root.infixSearch(no);
if(helper==null) {
throw new RuntimeException("没有找到目标节点");
}
return helper;
}
/**
* 后序查找
* @param no 目标节点编号
* @return 目标节点
*/
public Node postSearch(int no) {
Node helper = this.root.postSearch(no);
if(helper==null) {
throw new RuntimeException("没有找到目标节点");
}
return helper;
}
/**
* 删除节点
* @param no 待删除的节点编号
*/
public void delete(int no) {
if(this.root==null) {
System.out.println("树为空");
return;
}
//如果待删的是根节点,则根节点置空
if(root.no==no) {
root = null;
return;
}
this.root.delete(no);
}
}
/**
* 树的节点
*
* @author laowa
*
*/
class Node {
int no;
String name;
/**
* 左子节点
*/
Node left;
/**
* 右子节点
*/
Node right;
public Node(int no, String name) {
this.no = no;
this.name = name;
}
@Override
public String toString() {
return "[no=" + no + "\tname=" + name + "]";
}
/**
* 先序遍历
*/
public void preOrder() {
// 1.打印当前节点
System.out.println(this);
// 2.如果左子树不为空,则向左递归遍历
if (this.left != null) {
this.left.preOrder();
}
// 3.如果有子树不为空,则向右递归遍历
if (this.right != null) {
this.right.preOrder();
}
}
/**
* 中序遍历
*/
public void infixOrder() {
// 1.如果左子树不为空,则向左递归遍历
if (this.left != null) {
this.left.infixOrder();
}
// 2.打印当前节点
System.out.println(this);
// 3.如果右子树不为空,则向右递归遍历
if (this.right != null) {
this.right.infixOrder();
}
}
/**
* 后序遍历
*/
public void postOrder() {
// 1.如果左子树不为空,则向左递归遍历
if (this.left != null) {
this.left.postOrder();
}
// 2.如果右子树不为空,则向右递归遍历
if (this.right != null) {
this.right.postOrder();
}
// 3.打印当前节点
System.out.println(this);
}
/**
* 前序查找
*
* @param no
* 目标节点的编号
* @return 目标节点
*/
public Node preSearch(int no) {
// 辅助节点,存储找到的目标节点
Node helper = null;
// 1.判断当前节点是否是目标节点
if (this.no == no) {
helper = this;
}
// 2.如果左子树不为空,且目标节点还没有找到,则向左子树递归查找
if (this.left != null && helper == null) {
helper = this.left.preSearch(no);
}
// 3.如果右子树不为空,且目标节点还没有找到,则向右子树递归查找
if (right != null && helper == null) {
helper = this.right.preSearch(no);
}
// 返回最终结果
return helper;
}
/**
* 中序查找
*
* @param no
* 目标节点的编号
* @return 目标节点
*/
public Node infixSearch(int no) {
// 辅助节点,存储找到的目标节点
Node helper = null;
// 1.如果左子节点不为空,则向左递归查找
if (this.left != null) {
helper = this.left.infixSearch(no);
}
// 2.如果左子树没找到目标节点,判断当前是否是目标节点
if (helper == null && this.no == no) {
helper = this;
}
// 3.如果左子树和当前当前节点都没有找到,则向右递归查找
if (helper == null && this.right != null) {
helper = this.right.infixSearch(no);
}
return helper;
}
/**
* 后序查找
*
* @param no
* 目标节点的编号
* @return 目标节点
*/
public Node postSearch(int no) {
// 辅助节点,存储找到的目标节点
Node helper = null;
// 1.如果左子节点不为空,则向左递归查找
if (this.left != null) {
helper = this.left.postSearch(no);
}
// 3.如果左子树和当前当前节点都没有找到,则向右递归查找
if (helper == null && this.right != null) {
helper = this.right.postSearch(no);
}
// 2.如果左子树没找到目标节点,判断当前是否是目标节点
if (helper == null && this.no == no) {
helper = this;
}
return helper;
}
/**
* 删除节点
* @param no 待删除节点编号
*/
public void delete(int no) {
//1.判断左节点是否是目标节点
if(this.left!=null&&this.left.no==no) {
this.left=null;
return;
}
//2. 如果左子树不为空,则向左递归删除
if(this.left!=null) {
this.left.delete(no);
}
//3. 判断右节点是否是目标节点
if(this.right!=null&&this.right.no==no) {
this.right=null;
return;
}
//4.如果有子树不为空则向右递归删除
if(this.right!=null) {
this.right.delete(no);
}
}
}
顺序存储二叉树
从数据存储来看,数组存储方式和树存储方式可以相互转换;顺序存储的数组在遍历的时候使用树的遍历方式
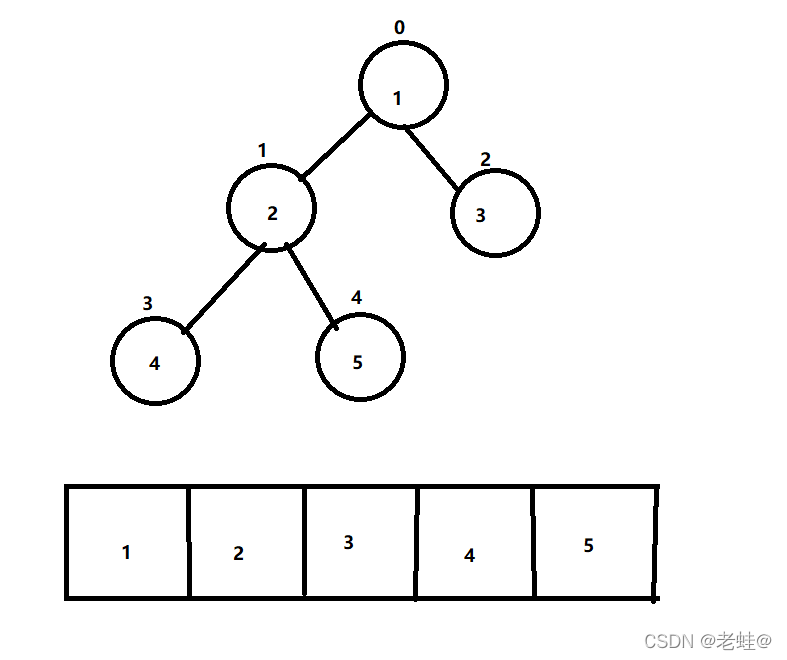
特点
- 顺序二叉树通常只考虑完全二叉树
- 第n个元素的左子节点为2n+1
- 第n个元素的右子节点为2n+2
- 第n个元素的父节点为(n-1)/2
代码实现
/***
* 顺序存储二叉树
* @author laowa
*
*/
class ArrayBinaryTree{
/**
* 存储数据节点的数组
*/
private int []arr;
public ArrayBinaryTree(int[] arr) {
this.arr = arr;
}
/**
* 先序遍历
*/
public void preOrder() {
preOrder(0);
}
/**
* 中序遍历
*/
public void infixOrder() {
infixOrder(0);
}
/**
* 后序遍历
*/
public void postOrder() {
postOrder(0);
}
/**
* 先序遍历
* @param index 根节点的索引
*/
private void preOrder(int index) {
//判空
if(arr==null||arr.length==0) {
System.out.println("空树");
return;
}
//输出当前元素
System.out.println(arr[index]);
//向左递归遍历,2*index+1即左子节点的索引
if((2*index+1)< arr.length) {
preOrder(2*index+1);
}
//向右递归遍历,2*index+2即右子节点的索引
if((2*index+2)<arr.length) {
preOrder(2*index+2);
}
}
/**
* 中序遍历
* @param index 根节点的索引
*/
private void infixOrder(int index) {
//向左子节点递归遍历
if((2*index+1)<arr.length) {
infixOrder(2*index+1);
}
//输出当前节点
System.out.println(arr[index]);
//向右子节点递归遍历
if((2*index+2)<arr.length) {
infixOrder(2*index+2);
}
}
/**
* 后序遍历
* @param index 根节点的索引
*/
private void postOrder(int index) {
//向左子节点递归遍历
if((2*index+1)<arr.length) {
postOrder(2*index+1);
}
//向右子节点递归遍历
if((2*index+2)<arr.length) {
postOrder(2*index+2);
}
//输出当前节点
System.out.println(arr[index]);
}
}
线索化二叉树
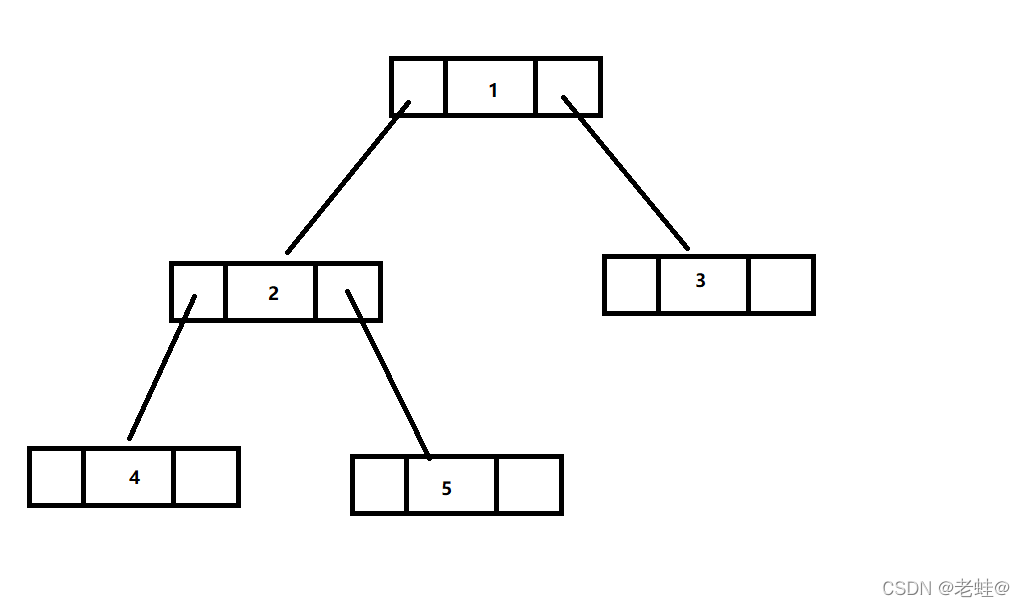
- 如上,在含有n个节点的二叉链表中含有n+1个空指针域(上方3,4,5三个节点的左右指针域),利用二叉链表中的空指针域,存放指向节点在某种遍历次序下的前驱和后继节点的指针(这种附加的指针称作线索),即二叉树的线索化
- 这种加上了线索的二叉链表称为线索链表,相应的二叉树称为线索二叉树。根据线索性质的不同,可以分为前序线索二叉树、中序线索二叉树、后序线索二叉树三种
- 在遍历中,某个节点前一个遍历的节点称为前驱节点,后一个称为后继节点
示意图
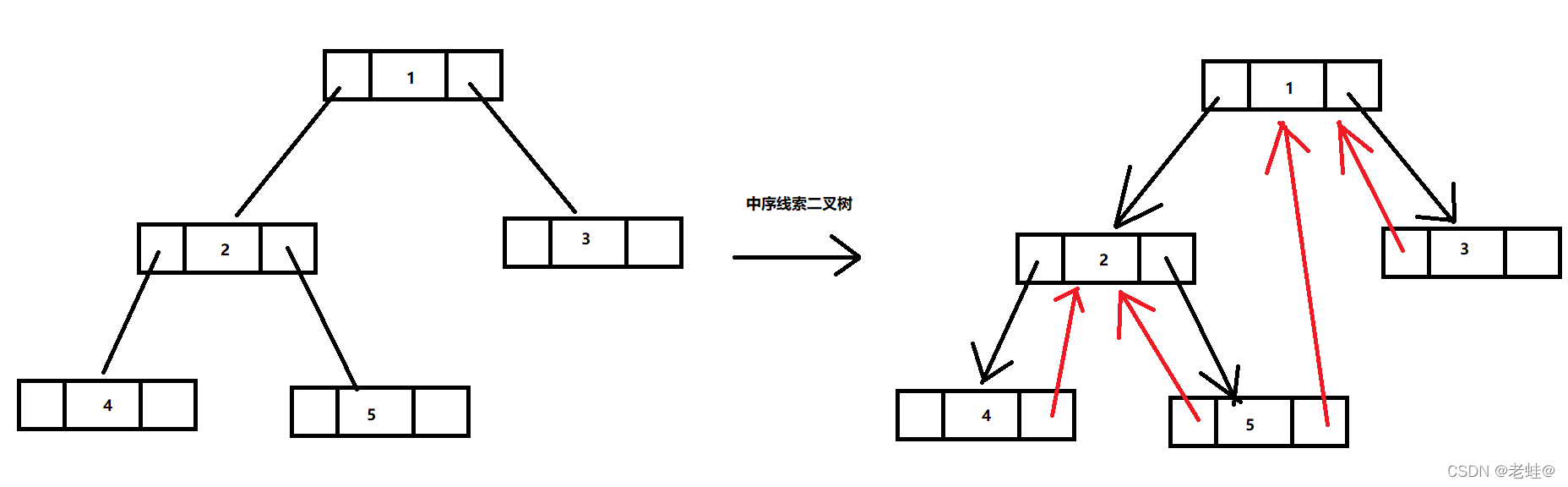
如上,线索化二叉树之后,Node节点的left和right有两种情况:
- left指向的是左子树,也有可能是指向前驱节点,比如1节点的left指向左子树,而5节点的left指向前驱节点
- right指向的是右子树,也有可能指向后继节点,比如1节点的right指向的是右子树,而5节点的right指向的是后继节点
代码实现(中序线索化)
/***
* 线索化二叉树
* @author laowa
*
*/
class ThreadBinaryTree{
/**
* 根节点
*/
Node root;
/**
* 为了实现线索化的辅助节点
* 因为二叉树是单向的,在进行线索化时,pre总是指向当前节点的前驱节点
*/
Node pre = null;
public ThreadBinaryTree(Node root) {
this.root = root;
}
/**
* 中序线索化二叉树
*/
public void infixThread() {
infixThreadNodes(root);
}
/**
* 对节点进行中序线索化
* @param node 需要线索化的节点
*/
public void infixThreadNodes(Node node) {
//判空,节点为null不能线索化
if(node==null) {
System.out.println("节点为空,不可线索化");
return;
}
//1. 向左递归线索化
if(node.left!=null) {
infixThreadNodes(node.left);
}
//2. 线索化当前节点
//如果当前节点的左指针为空,则将左指针指向前驱节点,然后将左指针的类型改为节点
if(node.left==null) {
node.left=pre;
node.leftType = Node.NODE;
}
//如果当前节点的前驱节点的右指针为空,则将前驱节点的后继节点指向当前节点,并且将右指针类型改为节点
if(pre!=null&&pre.right==null) {
pre.right = node;
pre.rightType = Node.NODE;
}
//每处理一个节点后,让pre指向当前节点,遍历到下一个节点后,pre就是前驱节点了
pre = node;
//3. 向右递归线索化
if(node.right!=null) {
infixThreadNodes(node.right);
}
}
}
/**
* 树的节点
*
* @author laowa
*
*/
class Node {
/**
* 表示指向子树
*/
public static final int CHILD_TREE=0;
/**
* 表示指向前驱或后继节点
*/
public static final int NODE=1;
int no;
String name;
/**
* 左子节点
*/
Node left;
/**
* 右子节点
*/
Node right;
/**
* 如果leftType为0,则表示指向的是左子树,如果leftType为1,表示指向前驱节点
*/
int leftType = Node.CHILD_TREE;
/**
* 如果rihgtType为0,则表示指向的是右子树,如果rightType为1,表示指向的是后继节点
*/
int rightType = Node.CHILD_TREE;
public Node(int no, String name) {
this.no = no;
this.name = name;
}
@Override
public String toString() {
return "[no=" + no + "\tname=" + name + "]";
}
}
中序线索化二叉树的遍历
/**
* 遍历中序线索化二叉树
*/
public void infixThreadList() {
// 辅助节点帮助遍历
Node helper = root;
// 当helper节点为空时退出循环
while (helper != null) {
// 向左找,一直找到leftType为node的节点,该节点就是最左侧叶子节点
while (helper.leftType == Node.CHILD_TREE) {
helper = helper.left;
}
// 输出当前节点
System.out.println(helper);
// 一直向右沿着线索化遍历,直到下一个节点的right非线索化
while (helper.rightType == Node.NODE) {
helper = helper.right;
System.out.println(helper);
}
// 当前节点的right非线索化,说明该节点不是叶子节点,且左侧的叶子节点已经遍历完了,直接向右移动一位
helper = helper.right;
}
}
前、中、后序线索化二叉树和遍历
/***
* 线索化二叉树
*
* @author laowa
*
*/
class ThreadBinaryTree {
/**
* 根节点
*/
Node root;
/**
* 为了实现线索化的辅助节点 因为二叉树是单向的,在进行线索化时,pre总是指向当前节点的前驱节点
*/
Node pre = null;
public ThreadBinaryTree(Node root) {
this.root = root;
}
/**
* 中序线索化二叉树
*/
public void infixThread() {
infixThreadNodes(root);
}
/**
* 前序线索化二叉树
*/
public void preThread() {
preThreadNodes(root);
}
/**
* 后序线索化二叉树
*/
public void postThread() {
postThreadNodes(root);
}
/**
* 遍历中序线索化二叉树
*/
public void infixThreadList() {
// 辅助节点帮助遍历
Node helper = root;
// 当helper节点为空时退出循环
while (helper != null) {
// 向左找,一直找到leftType为node的节点,该节点就是最左侧叶子节点
while (helper.leftType == Node.CHILD_TREE) {
helper = helper.left;
}
// 输出当前节点
System.out.println(helper);
// 一直向右沿着线索化遍历,直到下一个节点的right非线索化
while (helper.rightType == Node.NODE) {
helper = helper.right;
System.out.println(helper);
}
// 当前节点的right非线索化,说明该节点不是叶子节点,且左侧的叶子节点已经遍历完了,直接向右移动一位
helper = helper.right;
}
}
/**
* 遍历先序线索化二叉树
*/
public void preThreadList() {
// 辅助节点帮助遍历
Node helper = root;
// 当helper节点为空时停止遍历
while (helper != null) {
// 当左节点不为叶子节点时,先输出,然后左移
while (helper.leftType != Node.NODE) {
System.out.println(helper);
helper = helper.left;
}
// 循环结束后到了最左侧的叶子节点,输出当前节点
System.out.println(helper);
// 根据线索化,依次遍历节点
while (helper.rightType == Node.NODE) {
helper = helper.right;
System.out.println(helper);
}
// 当当前节点的right非线索化
helper = helper.right;
}
}
/**
* 遍历后序线索化二叉树
*/
public void postThreadList() {
postListNode(root);
}
/**
* 遍历后序线索化节点
* @param node
*/
private void postListNode(Node node) {
//向左递归直到叶子节点
if(node.leftType==Node.CHILD_TREE) {
postListNode(node.left);
}
//向右递归直到叶子节点
if(node.rightType==Node.CHILD_TREE) {
postListNode(node.right);
}
//输出当前节点
System.out.println(node);
}
/**
* 对节点进行中序线索化
*
* @param node
* 需要线索化的节点
*/
public void infixThreadNodes(Node node) {
// 判空,节点为null不能线索化
if (node == null) {
return;
}
// 1. 向左递归线索化
infixThreadNodes(node.left);
// 2. 线索化当前节点
// 如果当前节点的左指针为空,则将左指针指向前驱节点,然后将左指针的类型改为节点
if (node.left == null) {
node.left = pre;
node.leftType = Node.NODE;
}
// 如果当前节点的前驱节点的右指针为空,则将前驱节点的后继节点指向当前节点,并且将右指针类型改为节点
if (pre != null && pre.right == null) {
pre.right = node;
pre.rightType = Node.NODE;
}
// 每处理一个节点后,让pre指向当前节点,遍历到下一个节点后,pre就是前驱节点了
pre = node;
// 3. 向右递归线索化
infixThreadNodes(node.right);
}
/**
* 对节点进行前序线索化
*
* @param node
* 待线索化的节点
*/
public void preThreadNodes(Node node) {
// 判空
if (node == null) {
return;
}
//标志量,如果当前进行了左指针的线索化则不在向左递归
boolean toLeft = true;
//标志量,如果当前进行了右指针的线索化则不再向右递归
boolean toRight = true;
// 1.将当前节点线索化
if (node.left == null) {
node.left = pre;
node.leftType = Node.NODE;
toLeft = false;
}
if (pre != null && pre.right == null) {
pre.right = node;
pre.rightType = Node.NODE;
toRight = false;
}
pre = node;
// 2.向左递归线索化
if (toLeft) {
preThreadNodes(node.left);
}
// 3.向右递归线索化
if(toRight) {
preThreadNodes(node.right);
}
}
/**
* 对节点进行后序线索化
*
* @param node
* 待线索化的节点
*/
public void postThreadNodes(Node node) {
// 判空
if (node == null) {
return;
}
// 1.向左递归线索化
postThreadNodes(node.left);
// 2.向右递归线索化
postThreadNodes(node.right);
// 3.将当前节点线索化
if (node.left == null) {
node.left = pre;
node.leftType = Node.NODE;
}
if (pre != null && pre.right == null) {
pre.right = node;
pre.rightType = Node.NODE;
}
pre = node;
}
}
/**
* 树的节点
*
* @author laowa
*
*/
class Node {
/**
* 表示指向子树
*/
public static final int CHILD_TREE = 0;
/**
* 表示指向前驱或后继节点
*/
public static final int NODE = 1;
int no;
String name;
/**
* 左子节点
*/
Node left;
/**
* 右子节点
*/
Node right;
/**
* 如果leftType为0,则表示指向的是左子树,如果leftType为1,表示指向前驱节点
*/
int leftType = Node.CHILD_TREE;
/**
* 如果rihgtType为0,则表示指向的是右子树,如果rightType为1,表示指向的是后继节点
*/
int rightType = Node.CHILD_TREE;
public Node(int no, String name) {
this.no = no;
this.name = name;
}
@Override
public String toString() {
return "[no=" + no + "\tname=" + name + "]";
}
}
