Pre-hash数组 + component-DFS
前言
题目约束既是问题的出现,也是解决问题的钥匙。利用好问题条件和特性,拆解问题并优化解法。
通过解数独来完成困难题的拆解与题解优化。
一、解数独
归类:Pre-hash数组 + component-DFS类型的题。
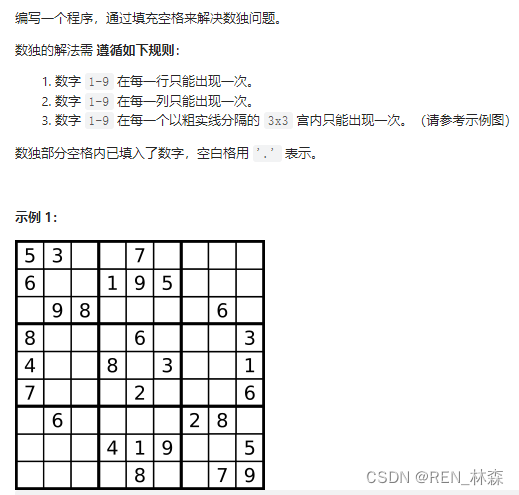

二、hash为DFS赋能
1、Pre-hash数组 + component-DFS
//解数独
public class SolveSudoku {
/*
target:在每一个为·的格子里填上一个1-9的数字,使其满足数独的条件。
数独成立条件:1-每个九宫格的数字为不重复的1-9;2-每行9个数分别为不重复的1-9;3-每列9个数分别为不重复的1-9.
问题刨析:那么一个位置就可以根据该位置所处九宫格、所处行、所处列,计算出该位置可选的值。
拿到可选的值开始DFS,dfs至最后一个空格完成没有返回false,说明该方案成功。否则退回重新规划路线。
M1:设置三个数组来记录每个格子的条件hash数组,然后一行一行的进行DFS。有点的位置被填充完值,回溯完应该赋值为点。
*/
public void solveSudoku(char[][] board) {
int[][] row = new int[9][9];
int[][] col = new int[9][9];
int[][][] grid = new int[3][3][9];
//设置hash数组的值
setHash(board, row, col, grid);
//DFS开始遍历
dfs(board, row, col, grid, 0, 0);
}
/**
* 进行模拟求解
*
* @param board
* @param row
* @param col
* @param grid
* @param i
* @param j
*/
private boolean dfs(char[][] board, int[][] row, int[][] col, int[][][] grid, int i, int j) {
int m = board.length, n = board[0].length;
//填充成功
if (i == m - 1 && j == n) return true;
//判断上一行是否遍历完
if (j == n) {
j = 0;
i = i + 1;
}
//填值
//非点的情况
boolean flag = false;
if (board[i][j] != '.') flag = dfs(board, row, col, grid, i, j + 1);
//是点,需要填值的情况。
else {
//用1-9来填
for (int k = 0; k < 9; k++) {
if (row[i][k] == 0 && col[j][k] == 0 && grid[i / 3][j / 3][k] == 0) {
board[i][j] = (char) (k + 1 + '0');
row[i][k] = 1;
col[j][k] = 1;
grid[i / 3][j / 3][k] = 1;
flag = dfs(board, row, col, grid, i, j + 1);
if (flag) return true;
//复原
board[i][j] = '.';
row[i][k] = 0;
col[j][k] = 0;
grid[i / 3][j / 3][k] = 0;
}
}
}
return flag;
}
/**
* 设置hash数组的值
*
* @param board
* @param row
* @param col
* @param grid
*/
private void setHash(char[][] board, int[][] row, int[][] col, int[][][] grid) {
int m = board.length, n = board[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] != '.') {
row[i][board[i][j] - '1']++;
col[j][board[i][j] - '1']++;
grid[i / 3][j / 3][board[i][j] - '1']++;
}
}
}
}
}
2、1-9二进制状态压缩
//用9位的二进制表示1-9是否出现过。
class SolveSudoku2 {
/*
M2:状态压缩--用9位的二进制表示1-9是否出现过。
左移运算 + 或运算 来得到该二进制。判断时通过位运算 + 与运算来判断该位是否为1,表示其出现过。
*/
public void solveSudoku(char[][] board) {
int[] row = new int[9];
int[] col = new int[9];
int[][] grid = new int[3][3];
//设置hash数组的值
setHash(board, row, col, grid);
//DFS开始遍历
dfs(board, row, col, grid, 0, 0);
}
/**
* 进行模拟求解
*
* @param board
* @param row
* @param col
* @param grid
* @param i
* @param j
*/
private boolean dfs(char[][] board, int[] row, int[] col, int[][] grid, int i, int j) {
int m = board.length, n = board[0].length;
//填充成功
if (i == m - 1 && j == n) return true;
//判断上一行是否遍历完
if (j == n) {
j = 0;
i = i + 1;
}
//填值
//非点的情况
boolean flag = false;
if (board[i][j] != '.') flag = dfs(board, row, col, grid, i, j + 1);
//是点,需要填值的情况。
else {
//用1-9来填
for (int k = 0; k < 9; k++) {
int val = 1 << k + 1;
if ((row[i] & val) == 0 && (col[j] & val) == 0 && (grid[i / 3][j / 3] & val) == 0) {
board[i][j] = (char) (k + 1 + '0');
row[i] |= val;
col[j] |= val;
grid[i / 3][j / 3] |= val;
flag = dfs(board, row, col, grid, i, j + 1);
if (flag) return true;
//复原
board[i][j] = '.';
row[i] -= val;
col[j] -= val;
grid[i / 3][j / 3] -= val;
}
}
}
return flag;
}
/**
* 设置hash数组的值
*
* @param board
* @param row
* @param col
* @param grid
*/
private void setHash(char[][] board, int[] row, int[] col, int[][] grid) {
int m = board.length, n = board[0].length;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] != '.') {
int val = 1 << board[i][j] - '0';
row[i] |= val;
col[j] |= val;
grid[i / 3][j / 3] |= val;
}
}
}
}
}
总结
1)利用问题的约束条件和目标来拆解问题。
2)利用问题的特性来完成题解的优化。
3)hash数组、DFS-递归回溯练习、二进制方式来状态压缩(新颖技巧)。
