区间问题
所谓区间问题,就是线段问题,让你合并所有线段、找出线段的交集等等。主要有两个技巧:
- 排序。常见的排序方法就是按照区间起点排序,或者先按照起点升序排序,若起点相同,则按照终点降序排序。当然,如果你非要按照终点排序,无非对称操作,本质都是一样的。
- 画图就是说不要偷懒,勤动手,两个区间的相对位置到底有几种可能,不同的相对位置我们的代码应该怎么去处理。
区间覆盖问题
Leetcode 1288 删除被覆盖区间

题目问我们,去除被覆盖区间之后,还剩下多少区间,那么我们可以先算一算,被覆盖区间有多少个,然后和总数相减就是剩余区间数。
对于这种区间问题,如果没啥头绪,首先排个序看看,比如我们按照区间的起点进行升序排序:
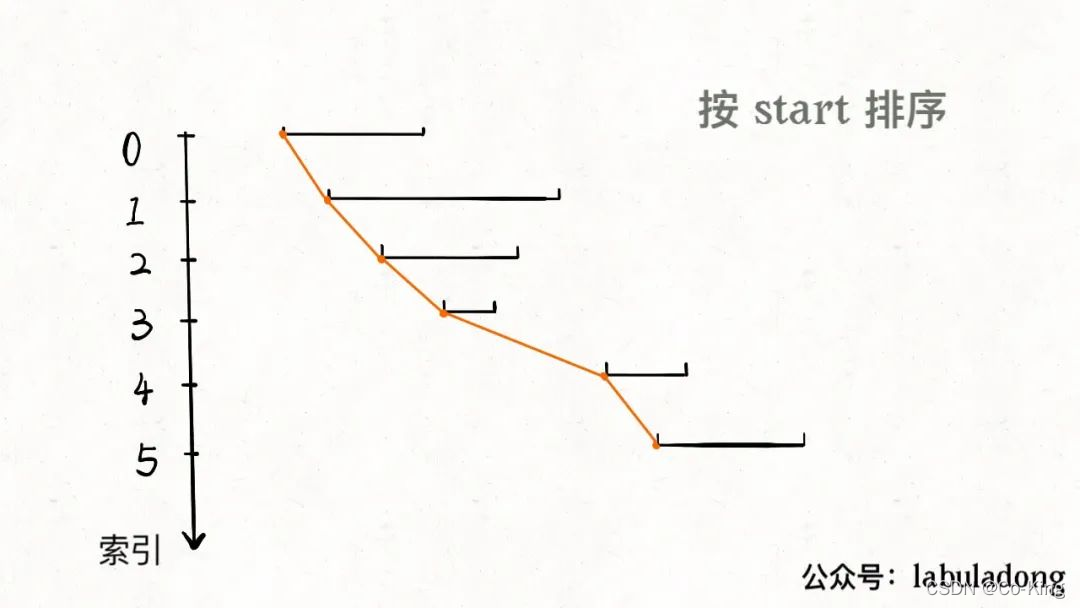
排序之后,两个相邻区间可能有如下三种相对位置:
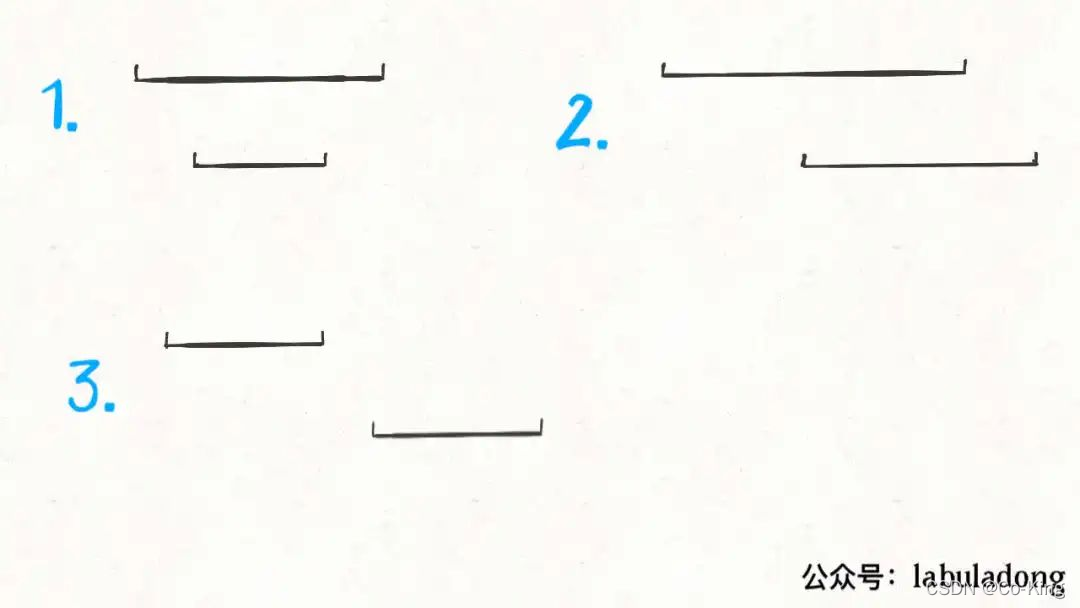
对于上面三种情况,我们应该进行如下处理:
- 情况一,找到了覆盖区间。
- 情况二,两个区间可以合并,成一个大区间。
- 情况三,两个区间完全不相交。
根据上面几种情况,我们可以写出如下代码:
int removeCoveredIntervals(int[][] intvs) {
// 按照起点升序排列,起点相同时降序排列
Arrays.sort(intvs, (a, b) -> {
if (a[0] == b[0]) {
return b[1] - a[1];
}
return a[0] - b[0];
});
// 记录合并区间的起点和终点
int left = intvs[0][0];
int right = intvs[0][1];
int res = 0;
for (int i = 1; i < intvs.length; i++) {
int[] intv = intvs[i];
// 情况一,找到覆盖区间
if (left <= intv[0] && right >= intv[1]) {
res++;
}
// 情况二,找到相交区间,合并
if (right >= intv[0] && right <= intv[1]) {
right = intv[1];
}
// 情况三,完全不相交,更新起点和终点
if (right < intv[0]) {
left = intv[0];
right = intv[1];
}
}
return intvs.length - res;
}
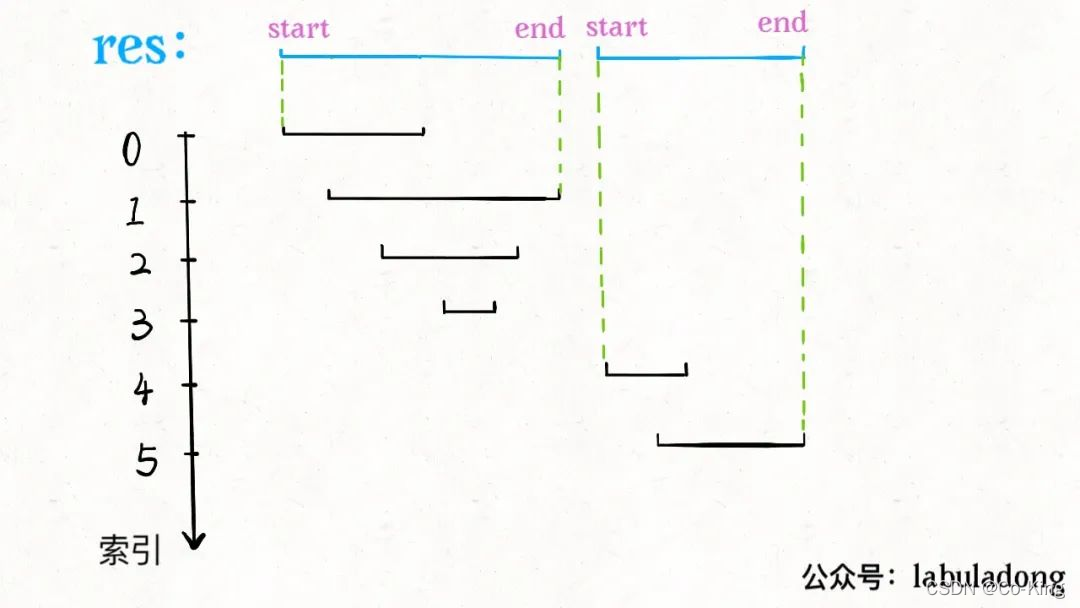
上面是本题的解法代码, 起点升序排列,终点降序排列的目的是防止如下情况的发生
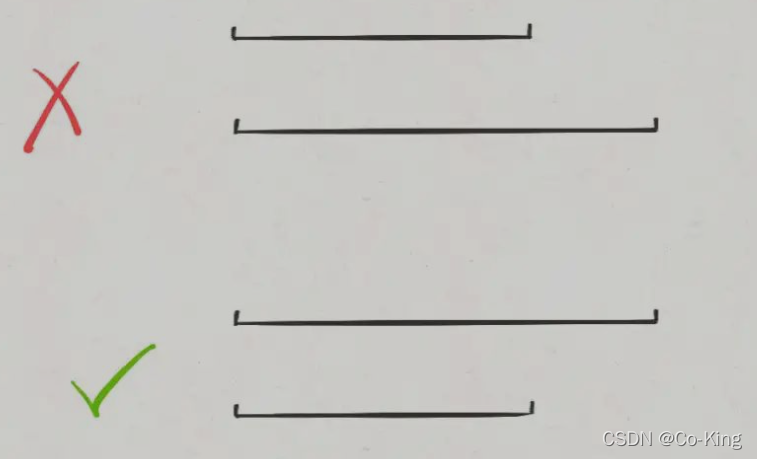
对于这两个起点相同的区间,我们需要保证长的那个区间在上面(按照终点降序),这样才会被判定为覆盖,否则会被错误地判定为相交,少算一个覆盖区间。
关于java当中二维数组的一些操作
// java创建一个二维数组
int[][] arr = {{1, 4}, {3, 6}, {2, 8}};
System.out.println(Arrays.toString(data)); // 使用这个方法可以打印出这个二维数组里面的每一个数组到底是什么
System.out.println(arr.length); // 3
int[] arr1 = arr[1];
System.out.println(arr1[0]); // arr1本身是一个地址值,但是通过取值里面的具体元素,可以得到的是数组里面的具体值
java当中的lambda函数
lambda函数表达式主要有四个例子
* - 1、不需要参数,返回值为5 () -> 5
* - 2、接收一个参数(数字类型),返回其2倍的值
* - 3、接收2个参数(数字),并返回他们的差值 (x, y) -> x – y
* - 4、接收2个int型整数,返回他们的和 (int x, int y) -> x + y
* - 5、接受一个 string 对象,并在控制台打印,不返回任何值(看起来像是返回void) (String s) -> System.out.print(s)
区间合并问题
Leetcode 56题,合并区间

解决区间问题的一般思路是先排序,然后观察规律。
一个区间可以表示为**[start, end]**,前文聊的区间调度问题,需要按end排序,以便满足贪心选择性质。而对于区间合并问题,其实按end和start排序都可以,不过为了清晰起见,我们选择按start排序。
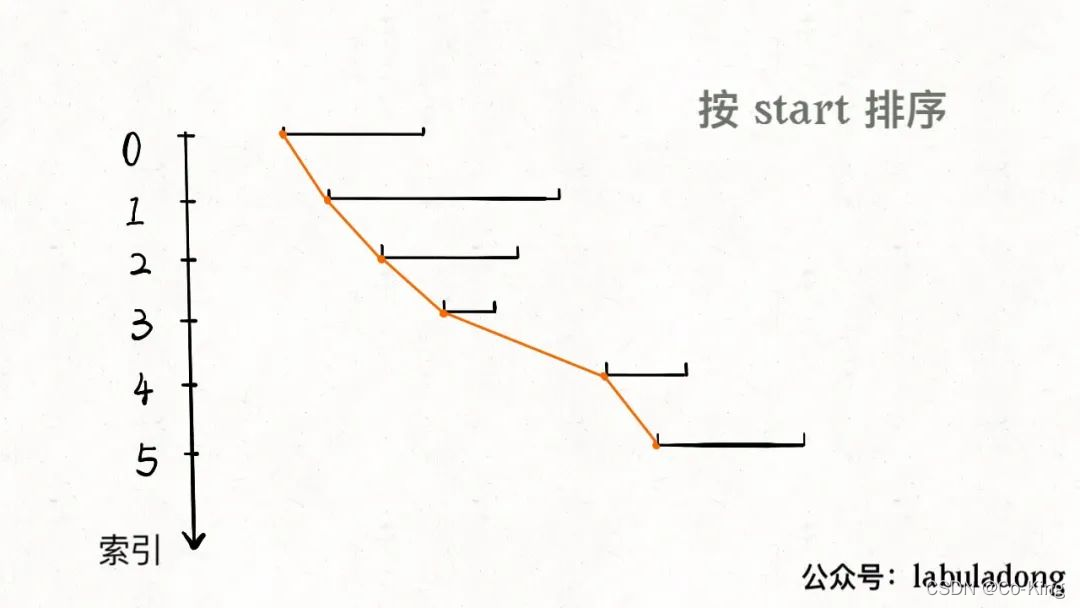
显然,对于几个相交区间合并后的结果区间x,x.start一定是这些相交区间中start最小的,x.end一定是这些相交区间中end最大的。
由于已经排了序,x.start很好确定,求x.end也很容易,可以类比在数组中找最大值的过程:
int max_ele = arr[0];
for (int i = 1; i < arr.length; i++)
max_ele = max(max_ele, arr[i]);
return max_ele;
完整代码 python
# intervals 形如 [[1,3],[2,6]...]
def merge(intervals):
if not intervals: return []
# 按区间的 start 升序排列
intervals.sort(key=lambda intv: intv[0])
res = []
res.append(intervals[0])
for i in range(1, len(intervals)):
curr = intervals[i]
# res 中最后一个元素的引用
last = res[-1]
if curr[0] <= last[1]:
# 找到最大的 end
last[1] = max(last[1], curr[1])
else:
# 处理下一个待合并区间
res.append(curr)
return res
java版本
class Solution {
public int[][] merge(int[][] intervals) {
LinkedList<int[]> res = new LinkedList<>();
// 按区间的 start 升序排列
Arrays.sort(intervals, (a, b) -> {
return a[0] - b[0];
});
res.add(intervals[0]);
for (int i = 1; i < intervals.length; i++) {
int[] curr = intervals[i];
// res 中最后一个元素的引用
int[] last = res.getLast();
if (curr[0] <= last[1]) {
last[1] = Math.max(last[1], curr[1]);
} else {
// 处理下一个待合并区间
res.add(curr);
}
}
// return res.toArray(new int[0][0]);
return res.toArray(new int[res.size()][];
}
}
toArray() 将一个集合转换为一个数组

区间交集问题
区间列表交集

题目很好理解,就是让你找交集,注意区间都是闭区间
解决区间问题的思路一般先排序,以便操作,不过题目说已经排好序了,那么可以用两个索引指针在A和B中游走,把交集找出来,
代码大概是这样的:
# A, B 形如 [[0,2],[5,10]...]
def intervalIntersection(A, B):
i, j = 0, 0
res = []
while i < len(A) and j < len(B):
# ...
j += 1
i += 1
return res
不难,我们先老老实实分析一下各种情况。
首先,对于两个区间,我们用[a1,a2]和[b1,b2]表示在A和B中的两个区间,那么什么情况下这两个区间没有交集呢:
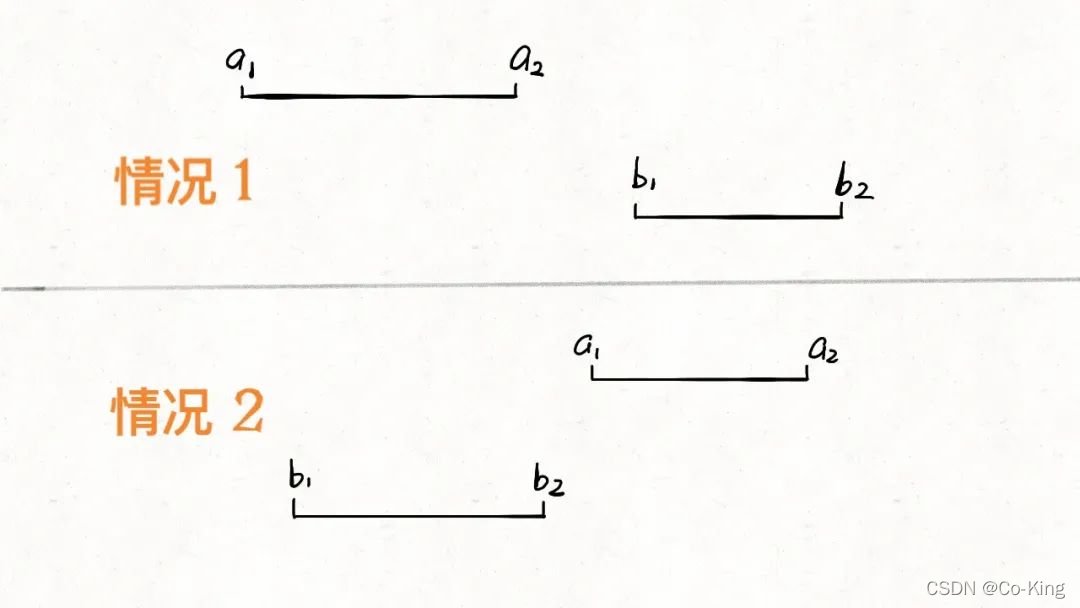
只有这两种情况,写成代码的条件是:
if b2 < a1 or a2 < b1:
[a1,a2] 和 [b1,b2] 无交集
那么,什么情况下,两个区间存在交集呢?根据命题的否定,上面逻辑的否命题就是存在交集的条件:
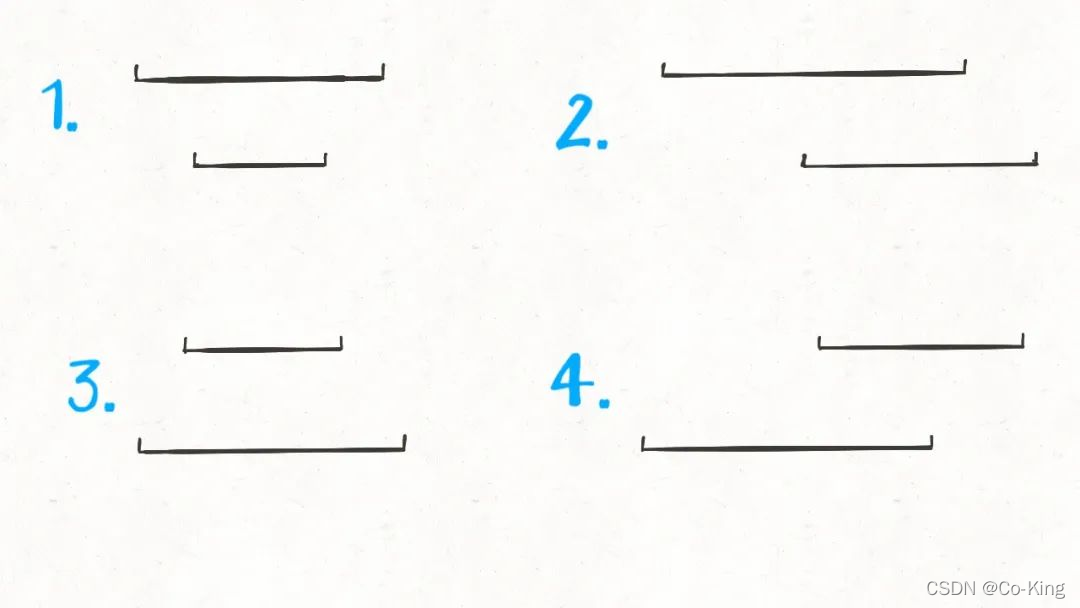
这很简单吧,就这四种情况**而已。那么接下来思考,这几种情况下,交集是否有什么共同点呢?
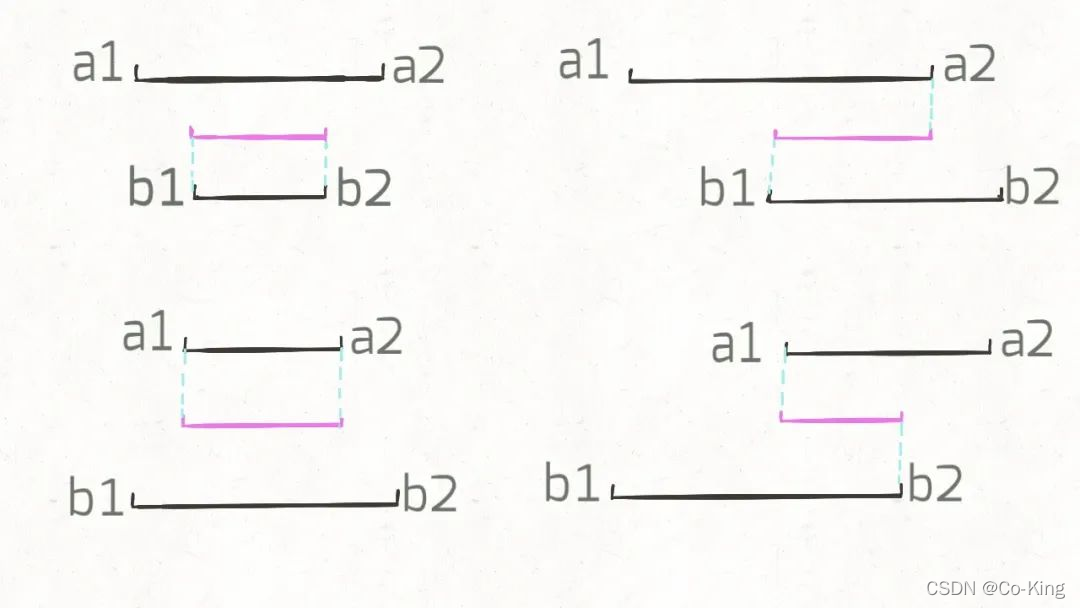
我们惊奇地发现,交集区间是有规律的! **如果交集区间是[c1,c2],那么c1=max(a1,b1),c2=min(a2,b2)!**这一点就是寻找交集的核心,我们把代码更进一步:
while i < len(A) and j < len(B):
a1, a2 = A[i][0], A[i][1]
b1, b2 = B[j][0], B[j][1]
if b2 >= a1 and a2 >= b1:
res.append([max(a1, b1), min(a2, b2)])
# ...
最后一步,我们的指针i和j肯定要前进(递增)的,什么时候应该前进呢?

结合动画示例就很好理解了,是否前进,只取决于a2和b2的大小关系:
while i < len(A) and j < len(B):
# ...
if b2 < a2:
j += 1
else:
i += 1
综上所述,代码实现
Python代码实现
# A, B 形如 [[0,2],[5,10]...]
def intervalIntersection(A, B):
i, j = 0, 0 # 双指针
res = []
while i < len(A) and j < len(B):
a1, a2 = A[i][0], A[i][1]
b1, b2 = B[j][0], B[j][1]
# 两个区间存在交集
if b2 >= a1 and a2 >= b1:
# 计算出交集,加入 res
res.append([max(a1, b1), min(a2, b2)])
# 指针前进
if b2 < a2: j += 1
else: i += 1
return res
Java代码实现
class Solution {
public int[][] intervalIntersection(int[][] A, int[][] B) {
List<int[]> res = new LinkedList<>();
int i = 0, j = 0;
while (i < A.length && j < B.length) {
int a1 = A[i][0], a2 = A[i][1];
int b1 = B[j][0], b2 = B[j][1];
if (b2 >= a1 && a2 >= b1) {
res.add(new int[]{
Math.max(a1, b1), Math.min(a2, b2)
});
}
if (b2 < a2) {
j++;
} else {
i++;
}
}
return res.toArray(new int[0][0]);
}
}
总结:
- 区间类问题看起来都比较复杂,情况很多难以处理,但实际上通过观察各种不同情况之间的共性可以发现规律,用简洁的代码就能处理。
