[数据结构与算法] leetcode222、完全二叉树的节点个数

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> leetcode222、完全二叉树的节点个数 -> 正文阅读

[数据结构与算法]leetcode222、完全二叉树的节点个数

题目描述

示例：
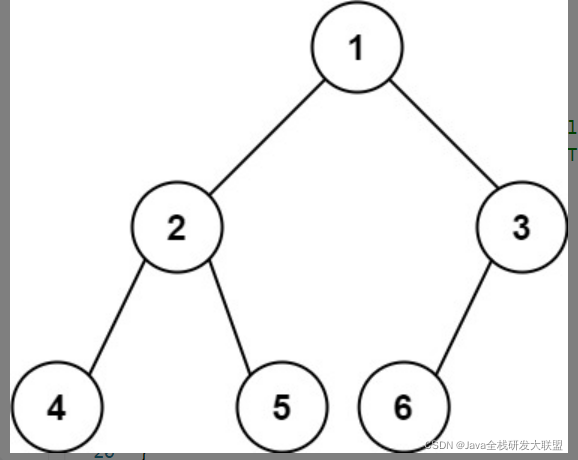
在这里插入图片描述

输入：root = [1,2,3,4,5,6]
输出：6

解法一：递归

凡是看到这种求二叉树的节点个数的问题，首先想到能不能用递归，然后如果能用递归的话，我们找出递归的逻辑。比如本题：
先确定单层循环逻辑: 先求它的左子树的节点数量，再求它的右子树的节点数量，最后取总和再加一（加1是因为算上当前中间节点）就是目前节点为根节点的节点数量。

int leftnum=_countNodes(root->left);
int rightnum=_countNodes(root->right);
int treenum=leftnum+rightnum+1;
return treenum;

然后我们要知道递归的终止条件,对于本题而言，终止的情况就是

if(root==nullptr)
{
  return 0;
}

所以很容易就能写出本题的答案代码

class Solution {
public:
    int countNodes(TreeNode* root) {
     if(root==nullptr)
     {
         return 0;
     }
     int left=countNodes(root->left);
     int right=countNodes(root->right);
     return left+right+1;
    }
};

时间复杂度：O(n) 空间复杂度：O(log n)

解法二：迭代，层序遍历

因为本题的树形结构比较特殊，是完全二叉树，所以我们可以想到通过层序遍历来解决，从树的根节点开始，一层一层的往下遍历，遍历到最后一层就可以数完所有的节点个数

代码如下: (注：层序遍历的实现方式一般使用queue队列来实现)

class Solution {
public:
    int countNodes(TreeNode* root) {
     if(root==nullptr)
     {
         return 0;
     }
     queue<TreeNode*> q;
     q.push(root);
     int result=0;
     while(!q.empty())
     {
         int size=q.size();
         for(int i=0;i<size;i++)
         {
             TreeNode* node=q.front();
             q.pop();
             result++;
             if(node->left) q.push(node->left);
             if(node->right) q.push(node->right);
         }
     }
     return result;
    }
};

时间复杂度：O(n) 空间复杂度：O(n)

如果本题要我们计算“满二叉树”的节点个数，那就更简单。
因为满二叉树的节点个数很容易通过树的高度来计算。满二叉树的节点个数= $2^n-1)$
代码也很好写：

int countNodes(TreeNode* root) {
    int h = 0;
    // 计算树的高度
    while (root != null) {
        root = root.left;
        h++;
    }
    // 节点总数就是 2^h - 1
    return (int)Math.pow(2, h) - 1;
}