“ Ctrl AC!一起 AC!”
对不起,本蒟蒻只会背模板...qwq
dijkstra一般用来解决单源最短路径问题,可以通过堆优化省去第二层找最近的那个点的循环。
pair版堆优化
开始用队列存储起点,然后利用优先队列对dis自动排序的功能,取出队头即为所要的最近点
typedef pair<int, int> PII; //first->distance; second->u;
priority_queue<PII, vector<PII>, greater<PII>> q;链式前向星
拿一个head数组存邻接表的头,也就是说head[u]存的是以连着u的所有边的一个链表的表头。
大概长这个样子(?)
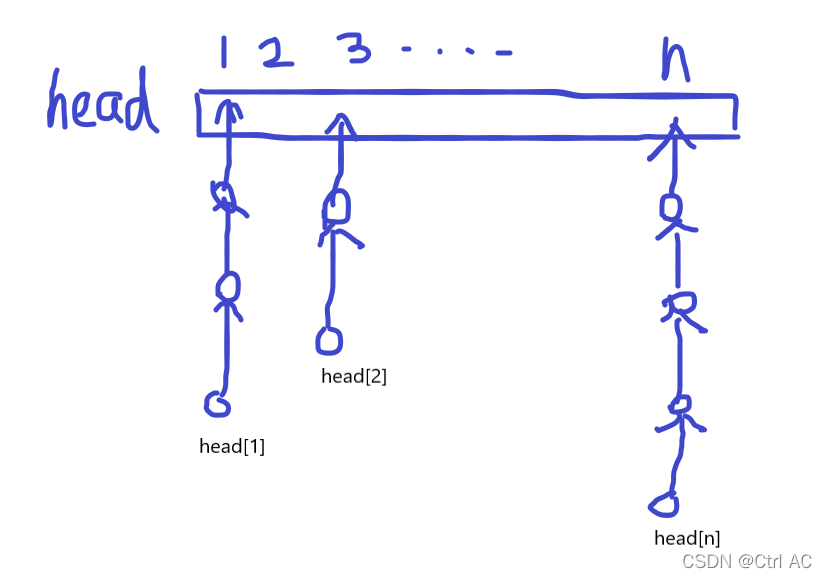
每个线段都是结点n的相关边,head[n]指的是最近加入的相关边(可以根据代码理解)
struct edge {
int v, w, nxt;
}e[M];
int head[N];
void addEdge(int u, int v, int w) {
static int cnt = 0;
e[++cnt] = { v,w,head[u] };
head[u] = cnt;
}全模板
配套题目:【洛谷】P4779 【模板】单源最短路径(标准版)
#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
typedef long long ll;
typedef pair<int, int> PII; //first->distance; second->u;
const int N = 100005;
const int M = 200005;
const int INF = 0x3f3f3f3f;
struct edge {
int v, w, nxt;
}e[M];
int head[N], dis[N];
void addEdge(int u, int v, int w) {
static int cnt = 0;
e[++cnt] = { v,w,head[u] };
head[u] = cnt;
}
priority_queue<PII, vector<PII>, greater<PII>> q;
void dij(int s) {
fill(dis, dis + N, INF);
dis[s] = 0;
q.push({ 0,s });
while (!q.empty() ){
int u = q.top().second, d = q.top().first; q.pop();
if (d != dis[u]) continue; //当且仅当d==dis[u]时,这个点u才是加入预备点!
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].v, w = e[i].w;
if (dis[u] + w < dis[v]) {
dis[v] = dis[u] + w;
q.push({ dis[v],v });
}
}
}
}
int main() {
int n, m, s; cin >> n >> m >> s;
for (int i = 1; i <= m; i++) {
int u, v, w; cin >> u >> v >> w;
addEdge(u, v, w);
}
dij(s);
for (int i = 1; i <= n; i++) cout << dis[i] << " ";
return 0;
}感谢阅读!!!
