用randX 实现 randY(X < Y)
其中,randN表示等概生成[1,N]的数
从一个力扣上的例子来引入吧
470. 用 Rand7() 实现 Rand10()
最直观的想法是用rand7()+rand7()-1去生成[1, 13]的数,然后只取[1, 10],但实际上这里的每个数并不是等概的,例如1的概率是1/49(1+1),但10的概率是4/49(4+7,5+6,6+5,7+4)。所以该方法并不可行。
事实上,可以把第一个rand7()和第二个rand7()分别看成两个独立的随机变量,假设分别为A和B,那么对于A∈[1,7]和B∈[1,7],可以作成一张二维表,一共有7*7=49种等概情况。
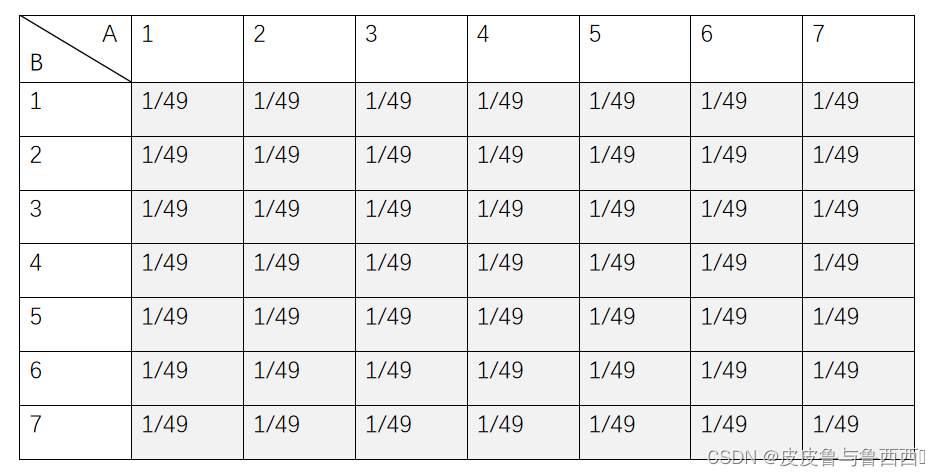
那么实际上我们只需在这49种情况中取出10种,其他的设为拒绝域(即不符合要求就重新采样)。但是这样设置,接收域概率太小了,可能导致我们的多次尝试。因此可以考虑对现有的49种情况归类,因为共10类,49/10=4…9,因此每类可以包含4种情况,剩下多出来的9类为拒绝域。
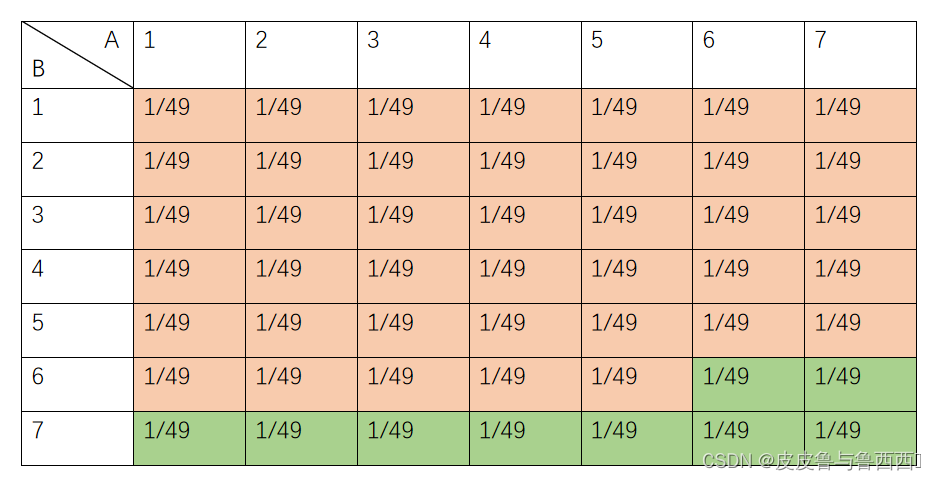
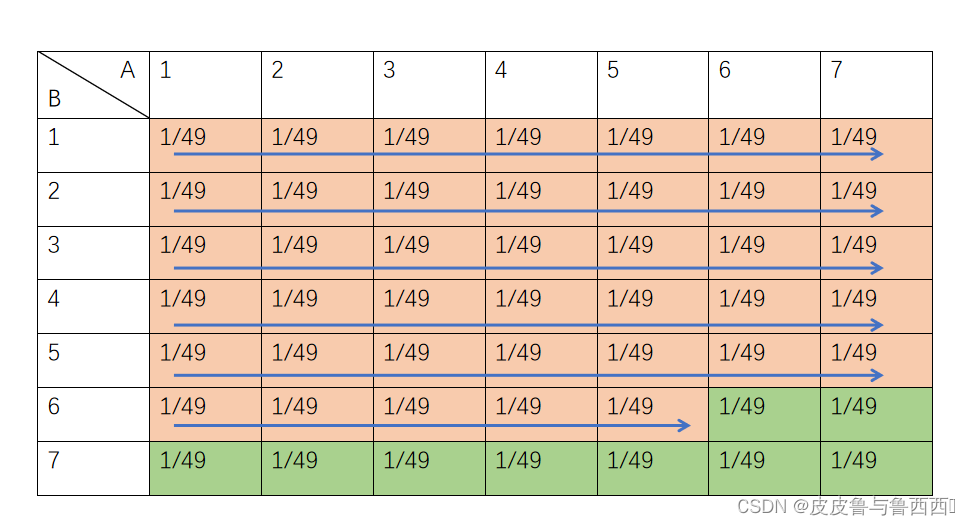
对于每种情况,我们需要进行一个编号,最简单的编号方法就是逐行从左到右编号。可以理解为,对于A=a,B=b,编号f(a,b)的映射为
f(a,b) = (a-1)*7 + b ∈[1,49]
这样就把所有情况映射到了区间[1,40]内(大于40的被舍弃)。
接着再对10取余,余数[0, 9]分别对应10种情况。
通过这种方式,可以最大化的利用出现概率。
深入分析
该问题的本质是对二元随机分布共7*7=49种情况去找一个合适的映射,等概地映射到10类。前面最直观的想法用rand7()+rand7()-1,实际上是找到映射f(a,b)=a+b ∈[2, 14],但这里值域的每个值的概率并不相等,所以这种映射是错误的。而用f(a,b)=(a-1)*7 + b 这种编号映射,十分直观,又可以最大化的利用概率。
合理映射不止一种,具体看如何设计了,例如,力扣某大佬设计出的下面这种,也是可以的(虽然多了一些拒绝域):

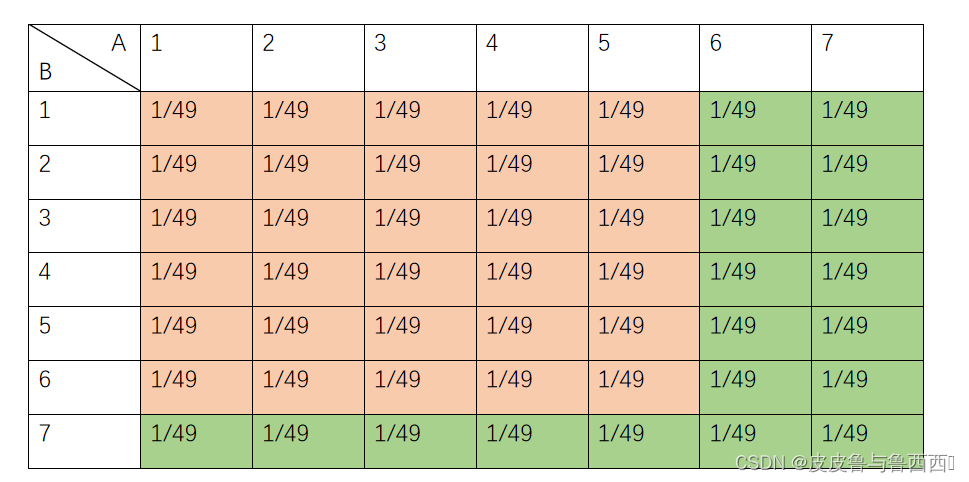
推广:用randX 和 randY实现 randXY(X < Y)
对于任意两个随机器 randX 和 randY,总共对应有XY种情况,可以组合成一个 randXY 的随机器,具体地:
randX*Y = (randX-1) * Y + randY
而任意的 randX,可以由其整数倍的随机器 randY = k*X 通过 下式得到
randX = randY % X + 1
用randY 实现 randX(Y>X)
若Y恰好是X的整数倍,则用上式即可;
若非整数倍,则先设置接收域和拒绝域,接收域为X的整数倍。那么取能够使得k*X<=Y的最大整数值k,充分扩大接收域范围。
例如在上面的例子中 rand49 -> rand10 ,取k=Y//10=3。
优化:充分利用拒绝域
在前面的例子中,对于位于拒绝域[41, 49]的元素,是采用直接抛弃的策略,重新生成随机数,这样效率是比较低的。但实际上,我们可以利用这个拒绝域,做一些延伸性的工作,尽可能提高命中概率。
对于不幸落于拒绝域的情况(元素超过40),可以认为其是一个rand9的随机生成器,那么可以再利用rand7,生成[1,63],然后取[1,60]为接收域,[61,63]为拒绝域。若再次不幸落于这个拒绝域中,我们又可以重复上一步的思路,认为这是一个rand3的随机器,利用rand7,生成[1,21],取[1,20]为接收域,[21,21]为拒绝域。此时若又不幸落于拒绝域21中,那么就是一个特定的数不再是随机数了。那么只能重头来过。
通过以上操作,我们可以算一下概率,三次都不命中的概率为:
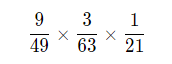
而如果不利用拒绝域,三次都不命中的概率为:
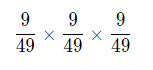
前者明显更小!!!
附一张官方题解计算的命中需调用rand7()次数的期望:
优化后:
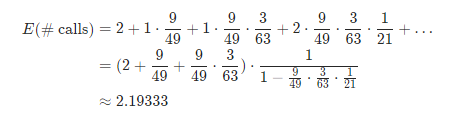
优化前:
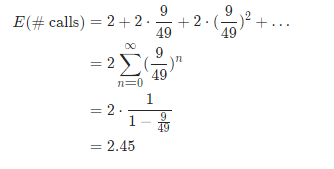
但这个是否是一个普适的结论,仍需严谨考证,也欢迎大家在下面留言一起讨论~
—————————————————————————————————————————————
参考:
从最基础的讲起如何做到均匀的生成随机数
官方题解:用 Rand7() 实现 Rand10()
