文章目录
实验一 后序非递归遍历
top=-1
//定义结构体
typedef struct satck
{
bintree data[100];
int tag[100];//定义一个标识
int top;
}seqstack;
//算法实现
void preorder1(bintreet)
{
seqsatck s;//在已经定义栈的情况下
init(&t);//置空栈
while(t||s.top!=-1)
{
if(t){//当前子树不为空的情况
push(&s,t);//入栈
s.tag[s.top]=0;//栈顶的标识改为0
t=t->lchild;//进入栈顶的左子树
}
else{
if(s.tag[s.top]==1)//右子树访问完成
{
t=pop(&s);//出栈
printf("%c",t->data);
t->NULL;//输出后,指针指向的还是这个结点,就变成了指针非空,但是前面指针非空是优先处理指针,所以主动将指针置为空,让它去栈里再取结点
}
else{//栈顶的标识是0,访问右指针
t=s.data[s.top];//去栈顶元,记录进入的右子树,栈顶地址
s.tag[s.top]=1;
t=t->rchild;
}
}
}
}
top=0
void preorder1(bintreet)
{
seqsatck s;//在已经定义栈的情况下
s.top=0;
while(t||s.top!=-1)
{
if(t){//当前子树不为空的情况
s.data[s.top]=t//第一三语句代表入栈,相当于push(&s,t);
s.tag[s.top]=0;//栈顶的标识改为0
s.top++;//因为top一开始是0,所以先入栈,栈顶元再加一
t=t->lchild;//进入栈顶的左子树
}
else{
if(s.tag[s.top-1]==1)//右子树访问完成,
//先入栈,栈顶元再加一,所以栈顶元总是多一个
{
s.top--;// 第一二语句代表出栈,相当于t=pop(&s)
t=s.data[s.top];
printf("%c",t->data);
t->NULL;//输出后,指针指向的还是这个结点,就变成了指针非空,但是前面指针非空是优先处理指针,所以主动将指针置为空,让它去栈里再取结点
}
else{//栈顶的标识是0,访问右指针
t=s.data[s.top-1];//去栈顶元,记录进入的右子树,栈顶地址
s.tag[s.top-1]=1;
t=t->rchild;
}
}
}
}
总结
定义一个栈并初始化,在指针不为空或栈顶不为空的情况下,分为子树不为空和子树为空。如果子树不为空,先进栈使top=0,然后将栈顶标识改为0,最后指向左子树。如果子树为空也要分两种情况。如果右子树访问完就出栈在打印,最后将指针赋值为空,否则将栈顶标识改为1,并指向右子树
实验二 前序非递归遍历
void preorder1(bintreet)
{
seqsatck s;//在已经定义栈的情况下
init(&s);
while(t||s.top!=-1)
{
if(t){
printf("%c",t->data);
push(&s,t);//入栈
t=t->lchild;//指向左指针
}
else{
t=pop(&s);//出栈
t=t->rchild;//指向右指针
}
}
}
总结
定义栈并初始化,在指针不为空或栈顶不为空的情况下,若子树不为空,先打印,再进栈,接着指向左子树,否则出栈指向右子树
实验三 中序非递归遍历
void preorder1(bintreet)
{
seqsatck s;//在已经定义栈的情况下
init(&s);
while(t||s.top!=-1)
{
if(t){//当前子树不为空的情况
push(&s,t);//入栈
t=t->lchild;//指向左指针
}
else{
t=pop(&s);//出栈
printf("%c",t->data);
t=t->rchild;//指向右指针
}
}
}
总结
与前序区别在于进入栈前不打印,出栈才打印
实验四 二叉树的层次遍历
/*
编写算法函数void levelbintree(bintree t),实现二叉树的层次遍历。
*/
#include "bintree.h"
char *a="ABC##D#E##F##"; /*扩充二叉树序树t的前序序列*/
void levelbintree(bintree t)
{
bintree quene[100];//定义数组
int f=0,r=1;
if(t)
{
quene[0]=t;//根结点
while(f<r)// 当f==r时,遍历到了最后子树,遍历结束
{
t=quene[f++];
printf("%c",t->data);
if(t->lchild)
{
quene[r++]=t->lchild;
}
if(t->rchild)
{
quene[r++]=t->rchild;
}
}
}
}
int main()
{ bintree t;
t=creatbintree(); /*建立二叉树t的存储结构*/
printf("二叉树的层次序列为:\n");
levelbintree(t); /*层次遍历二叉树*/
return 0;
}
总结
当树不为空,前面数组小标小于后面时循环,r记录叶子结点,最后遍历可以分别遍历每一层的左右结点
实验五 返回前序遍历下的最后一个结点地址和后序遍历下的第一个结点地址
/*
编写函数bintree prelist(bintree t),bintree postfirst(bintree t),
分别返回二叉树t在前序遍历下的最后一个结点地址和后序遍历下的第一个结点地址。
*/
#include "bintree.h"
char *a="ABC##D##EF#G###"; /*扩充二叉树序树t的前序序列*/
bintree prelast(bintree t)
{//递归
if(!t)
{
return t;//没找到结点
}
else if(t->lchild==NULL&&t->rchild==NULL)//找到
{
return t;
}
else
{
if(t->rchild)//右子树非空
{
prelast(t->rchild);
}
else
{
prelast(t->lchild);
}
}
}
bintree postfirst(bintree t)
{//非递归
bintree p;
p=t;//非递归会改变t的
if(p)
{
while(p->rchild||p->lchild)
{
if(p->lchild)
{
p=p->lchild;
}
else if(p->rchild)
{
p=p->rchild;
}
}
}
return p;
}
int main()
{ bintree t,p,q;
t=creatbintree(); /*建立二叉树t的存储结构*/
p=prelast(t);
q=postfirst(t);
if (t!=NULL)
{ printf("前序遍历最后一个结点为:%c\n",p->data);
printf("后序遍历第一个结点为:%c\n",q->data);
}
else printf("二叉树为空!");
return 0;
}
总结
- 递归遍历先判断树是否为空,是否为叶子结点,因为找最后一个结点地址,所以 先看是否有左结点,否则再去找右结点
- 非递归遍历在树不空的基础上看左右子树是否都存在,因为是后序第一个结点,所以先往左找,没有再往右找。当都不存在就是找到了
实验六 链式存储二叉树,求值为x的结点在二叉树中的层次
递归算法
/*
假设二叉树采用链式方式存储,t为其根结点,编写一个函数int Depth(bintree t, char x),求值为x的结点在二叉树中的层次。
*/
#include "bintree.h"
char *a="ABC##D##EF#G###"; /*扩充二叉树序树t的前序序列*/
/*
函数Depth,功能:求结点x所在的层次
*/
int Depth1(bintree t,char x)
{
if(!t) return -1;//递归根结点,此路不通
if(t->data==x) return 1;//找到了
int hl=Depth1(t->lchild,x);
int hr=Depth1(t->rchild,x);
if(hl!=-1) return hl+1;
if(hr!=-1) return hr+1;
return -1;
}
int main()
{ bintree root;
char x;
int k=0;
root=creatbintree();
printf("请输入树中的1个结点值:\n");
scanf("%c",&x);
k=Depth1(root,x);
printf("%c结点的层次为%d\n",x,k);
}
总结
只要为空就返回-1,然后在左右子树递归寻找,若找到返回的就不是-1,那么这个时候不停+1得到最终层数
非递归算法
/*
假设二叉树采用链式方式存储,t为其根结点,编写一个函数int Depth(bintree t, char x),求值为x的结点在二叉树中的层次。
*/
#include "bintree.h"
char *a="ABC##D##EF#G###"; /*扩充二叉树序树t的前序序列*/
/*
函数Depth,功能:求结点x所在的层次
*/
int Depth2(bintree t,char x)
{
seqstack s;
int tag[100];
while(t||s.top!=-1)
{
if(t)
{
push(&s,t);
s.tag[s.top]=0;
t=t->lchild;
}
else
{
if(s.tag[s.top]==1)
{
t=pop(&s);
if(t->data==x)
{
return s.top+2;//本来是+1,但是top=-1
}
t=NULL;
}
else
{
t=s.data[s.top];
s.tag[s.top]=1;
t=t->rchild;
}
}
}
}
int main()
{ bintree root;
char x;
int k=0;
root=creatbintree();
printf("请输入树中的1个结点值:\n");
scanf("%c",&x);
k=Depth2(root,x);
printf("%c结点的层次为%d\n",x,k);
}
总结
后序非递归遍历中,在出栈的时候判断是否为选的结点,如果是,将栈顶+2就是层数。
出栈后本来应该是栈减了一位,所以先+1,又因为top一开始定义-1,所以+2
实验七-输出叶子结点
void leaf(bintreet)
{
seqsatck s;
init(&t);
while(t||s.top!=-1)
{
if(t){
if(!t->lchild&&!t->rchild)
{
printf("%c",t->data);//输出叶子
}
push(&s,t);
s.tag[s.top]=0;
t=t->lchild;
}
else{
if(s.tag[s.top]==1)
{
t=pop(&s);
printf("%c",t->data);
t->NULL;
}
else{
t=s.data[s.top];
s.tag[s.top]=1;
t=t->rchild;
}
}
}
}
总结
在后序非递归遍历中只用在入栈前加个条件判断是否左右指针都为空,然后输出,则为叶子结点
实验八-穿线二叉树
创建并进行线索化
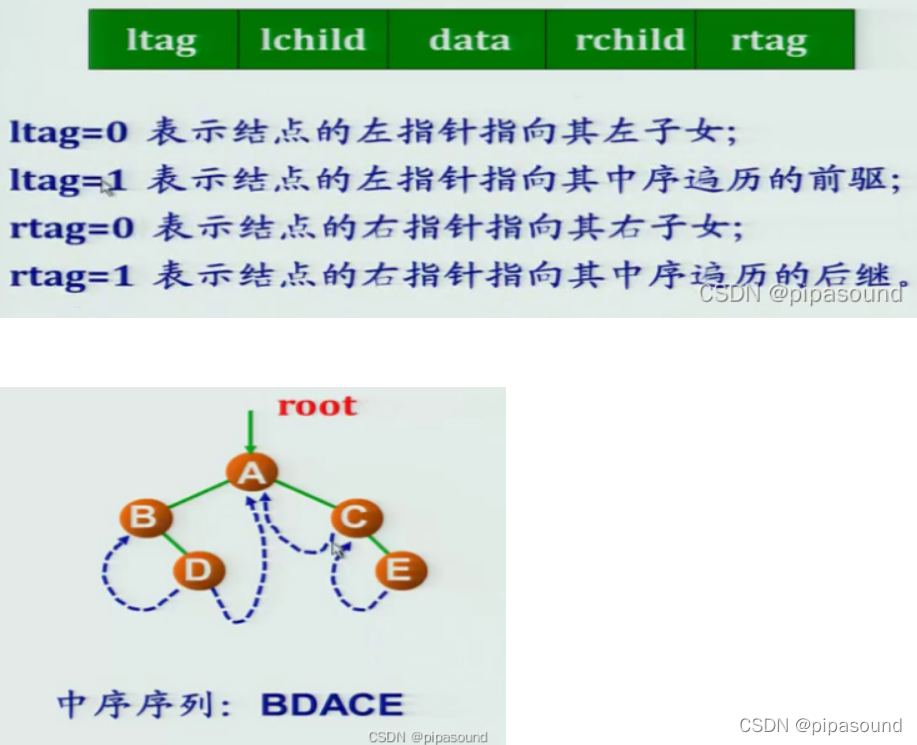
typedef char datatype;//结点属性值的类型
typedef struct node{//二叉树节点类型
datatype data;
int ltag,rlag;//增加左右指针标识
struct node *lchild,*rchild;
}bintnode;//二叉树
typedef bintnode *binthrtree;//指向二叉树结点的指针类型
//bintnode *等价struct node*
/********创建中序穿线二叉树*********/
binthrtree pre=NULL;//我们需要两个指针,这个指针代表遍历这个结点的前驱结点。因为每次递归都要调用,设为全局变量
binthrtree createbinthrtree()
{
char ch;
binthrtree t;
if((ch=getchar())=='#')
t=NULL;
else{
t=(bintnode *)malloc(sizeof(bintnode));
t->data=ch;//建立子树根结点
t->lchild=createbinthrtree();
t->rchild=createbinthrtree();
}
return t;
}
/****对二叉树进行线索化****/
void inthreading(binthrtree *p)
{
if(*p)//只要不是空树
{
inthreading(&((*p)->lchild));//先遍历左子树
(*p)->ltag=((*p)->lchild)?0:1;//判断左子树是否空后把0or1赋给标识
(*p)->rtag=((*p)->rchild)?0:1;
if(pre)//前驱结点存在
{
if(pre->rtag==1) pre->rchild=*p;//指向后继
if((*p)->ltag==1) (*p)->lchild=pre;//指向前驱
}
inthreading(&((*p)->rchild));//再遍历右子树
}
}
找中序首点
void inthrtree(binthtree p)
{
if(p)
{
while(p->ltag==0)
p=p->lchild;
}
}
总结
从根结点出发,沿着左指针不断往下走,直到左指针为空,到达“”最左下“的结点即可
找中序后继结点
binthtree insuccnode(binthrtree p)
{
binthrtree q;
if(p->rtag==1) return p->rchild;//当标识为1,后面的结点就是中序后继结点,看图一
else{//标识不为1,证明还有右子树,如图2
q=p->rchild;//进入右子树,右子树的首结点就是后继结点
while(q->ltag==0)//向左往下滑,直到左指针为空,到达右子树首点
{
q=q->lchild;
}
return q;
}
}
总结
找后继结点分两种情况,一种是右标识为1,后面结点就是后继结点,另一种是右标识不为0,说明还有右子树,那就遍历右子树找到其首点,这个点才是后继结点
-
图1
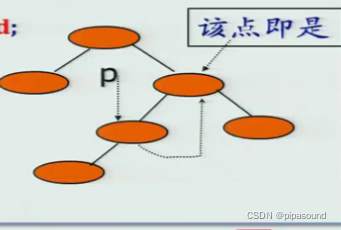
-
图2
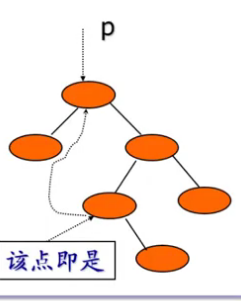
中序遍历中序穿线二叉树
void inthrtree(binthtree p)
{
if(p)
{
while(p->ltag==0)
p=p->lchild;
do
{
printf("%c",p->data);
p=insuccnode(p);
}while(p)
}
}
总结
先找到首点,打印后递归输出后继结点,实现遍历
穿线二叉树完整过程
typedef char datatype;//结点属性值的类型
typedef struct node{//二叉树节点类型
datatype data;
int ltag,rlag;//增加左右指针标识
struct node *lchild,*rchild;
}bintnode;//二叉树
typedef bintnode *binthrtree;//指向二叉树结点的指针类型
//bintnode *等价struct node*
/********创建中序穿线二叉树*********/
binthrtree pre=NULL;//我们需要两个指针,这个指针代表遍历这个结点的前驱结点。因为每次递归都要调用,设为全局变量
binthrtree createbinthrtree()
{
char ch;
binthrtree t;
if((ch=getchar())=='#')
t=NULL;
else{
t=(bintnode *)malloc(sizeof(bintnode));
t->data=ch;//建立子树根结点
t->lchild=createbinthrtree();
t->rchild=createbinthrtree();
}
return t;
}
/****对二叉树进行线索化****/
void inthreading(binthrtree *p)
{
if(*p)//只要不是空树
{
inthreading(&((*p)->lchild));//先遍历左子树
(*p)->ltag=((*p)->lchild)?0:1;//判断左子树是否空后把0or1赋给标识
(*p)->rtag=((*p)->rchild)?0:1;
if(pre)//前驱结点存在
{
if(pre->rtag==1) pre->rchild=*p;//指向后继
if((*p)->ltag==1) (*p)->lchild=pre;//指向前驱
}
inthreading(&((*p)->rchild));//再遍历右子树
}
}
/************找中序后继结点************/
binthtree insuccnode(binthrtree p)
{
binthrtree q;
if(p->rtag==1) return p->rchild;//当标识为1,后面的结点就是中序后继结点,看图一
else{//标识不为1,证明还有右子树,如图2
q=p->rchild;//进入右子树,右子树的首结点就是后继结点
while(q->ltag==0)//向左往下滑,直到左指针为空,到达右子树首点
{
q=q->lchild;
}
return q;
}
}
/*************遍历*************/
void inthrtree(binthtree p)
{
if(p)
{
while(p->ltag==0)
p=p->lchild;
do
{
printf("%c",p->data);
p=insuccnode(p);
}while(p)
}
}
int main()
{
bintree t;
t=creatbintree();
printf("穿线二叉树的中序遍历为:\n");
inthrtree(t);
return 0
}
实验九 所有结点的左、右子女互换
/*
试编写一个函数,将一棵给定二叉树中所有结点的左、右子女互换。
*/
#include "bintree.h"
char *a="ABC##D##EF#G###"; /*扩充二叉树序树t的前序序列*/
/*请将本函数补充完整,并进行测试*/
void change(bintree t)
{
bintree tmp;
if(t)
{
tmp=t->lchild;
t->lchild=t->rchild;
t->rchild=tmp;
change(t->lchild);
change(t->rchild);
}
}
int main()
{ bintree root;
root=creatbintree();
change(root);
preorder(root);
}
总结
在树存在的情况下先将左右结点互换,然后再递归遍历左右子树
实验十 层次遍历寻找树的最大宽度
#include "bintree.h"
char *a="ABD##EH##I##CF##G##";
//利用层次遍历找树的最大宽度
//顺序队
typedef struct{
bintree qu[N];
int level[N];
int f,r;//定义首尾指针
}seqQuene;
//入队
void push1(seqQuene* q,bintree x)
{
q->qu[q->r++]=x;//指向后指针
}
//出队
bintree pop1(seqQuene* q)
{
return q->qu[q->f];//指向前指针
}
int wepth(bintree t)
{
int max=0;//最大宽度
seqQuene q;
q.f=q.r=NULL;//初始化
if(t)
{
//等同于q.qu[q.r++]=t;
push1(&q,t);
}
while(q.f<q.r)//里面有元素
{
int tm=q.r;
int stmax=0;
for(q.f;q.f<tm;q.f++)
{
bintree tmp=pop1(&q);
if(tmp->lchild)
{
//q.qu[q.r++]=q.qu[q.f]->rchild;
push1(&q,tmp->rchild);
}
stmax++;
}
if(stmax>max)
{
max=stmax;
}
q.f=tm;
}
return max;
}
int main()
{ bintree t;
t=creatbintree(); /*建立二叉树t的存储结构*/
printf("二叉树的度数为:\n");
wedth(t);
return 0;
}
bintree.h
#include <stdio.h>
#include <stdlib.h>
#define N 100
extern char *a; /*存放扩充二叉树的前序序列*/
typedef struct node /*二叉树结构定义*/
{
char data;
struct node *lchild,*rchild;
}binnode;
typedef binnode *bintree;
/*函数creatbintree (根据扩充二叉树的前序序列(字符串a)建立二叉树t的存储结构*/
bintree creatbintree()
{
char ch=*a++;
bintree t;
if (ch=='#') t=NULL;
else
{ t=(bintree)malloc(sizeof(binnode));
t->data=ch;
t->lchild=creatbintree();
t->rchild=creatbintree();
}
return t;
}
void preorder(bintree t) /*前序递归遍历二叉树*/
{
if (t)
{
printf("%c",t->data);
preorder(t->lchild);
preorder(t->rchild);
}
}
void postorder(bintree t) /*后序递归遍历二叉树*/
{
if (t)
{
postorder(t->lchild);
postorder(t->rchild);
printf("%c",t->data);
}
}
/*顺序栈定义*/
typedef struct
{
bintree data[N];
int top;
int tag[N];
}seqstack;
void init(seqstack *s) /*初始化空栈*/
{
s->top=-1;
}
int empty(seqstack *s) /*判断栈是否为空*/
{
if (s->top>-1) return 0;
else return 1;
}
int full(seqstack *s) /*判断栈是否为满*/
{
if (s->top==N-1) return 1;
else return 0;
}
void push(seqstack *s ,bintree x) /*进栈*/
{
if (!full(s))
s->data[++s->top]=x;
}
bintree pop(seqstack *s) /*出栈*/
{
if (!empty(s))
return s->data[s->top--];
}
