解题思路
1.题目描述
给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成。
示例1
输入: s = “abab”
输出: true
解释: 可由子串 “ab” 重复两次构成。
示例2:
输入: s = “aba”
输出: false
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/repeated-substring-pattern
2.题目分析
2.1 暴力枚举
假设有字符串fStr,它是由短字符串sStr重复组成的,而且fStr的长度为N,sStr的长度为n,那么就有以下等式成立。同理如果下面的规律满足则必然是由sStr重复而构成fStr。所以下面的条件是是否是重复子串构成的充要条件。
fStr[i] = fStr[i+n]
N % n == 0
以下图中的以子串"abc"重复构成的字符串为例,子串"abc"长度为3,字符串长度为9,所以有9%3==0,并且在不越界的情况下对于每个str[i]总有str[i]==str[i+3]。所以我们便可以根据这个规律进行枚举解题。
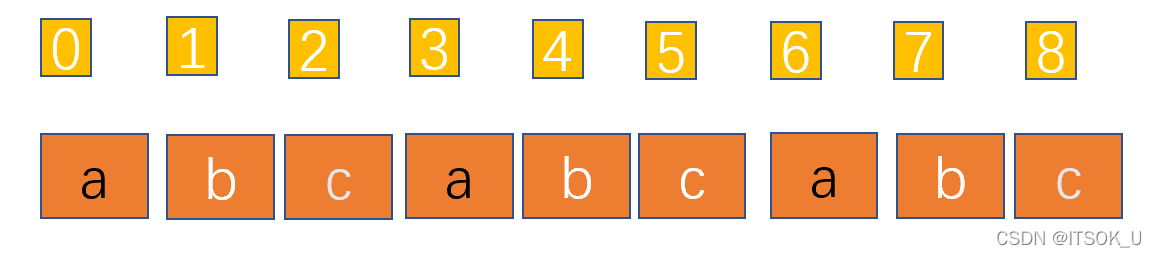
具体解题思路如下,我们首先从小到大假设出所有的可能组成字符串的子串的长度,然后通过上面的规律依次进行条件判断,如果是成立的,那么字符串就是由这个循环子串组成的,否则判断下一个长度的子串,直到长度不能满足构成重复的条件(也就是说子串长度最大为字符串的1/2)。
2.2 KMP算法解题
本题其实还是一个字符串匹配的问题。如果一个长度为len的字符串是由长度为w重复子串构成的,那么那么我们就可以得出重复子串的长度w等于len-(next[len-1]+1)。下面对这个公式做一个说明;
2.2.1 周期串必是多个重复字串
按照题目要求,我们可以知道一个周期穿必然是由多个重复子串组成的,以下面的这个字符串为例,我们可以得出其next[8]=6,我们可以计算出子串长度为9-(next[8])=3。这样我们就得出对于一个重复串必然有w=len-(next[len-1])

2.2.2 w=len-(next[len-1])–>是周期串
2.3 使用库函数
既然是判断字符串是否由重复子串组成,那么我们必然可以通过n次循环移位使得字符串又等于它本身,如上面的字符串进行循环移位的状态转移就会是
abcabcabc ---->bcabcabca—>cabcabcabcab—>abcabcabc
我们会发现这个次数n就是字符串的子串的长度。我们当然可以通过这种朴素的移位来进行判断是否满足题设条件,但是我们知道对于string与vector这两种数据结构来说,这样移动元素的开销极大,所以我们要尽可能的减少此类操作。
2.3.1 必要性
接着上面的分析,我们假设母串Str是由子串s重复N次而成, 则 Str+Str则有子串s重复2N次, 那么现在就有: Str=N*s, Str+Str=2N*s, 其中N>=2。 如果条件成立, Str+Str掐头去尾会破坏2个s, Str+Str中还包含2*(N-1)s, 又因为N>=2, 因此 Str在去掉首尾两个元素的(Str+Str)中必会出现一次以上。而且第一次出现必然是位于 Str+Str字符串的前半部分,最后一次出现必然是Str.size()位置开始的最后一个Str。这样我们就说明了必要性。

2.3.2 充分性
假设有一个一般串,我们对其进行上述的拼接,并掐去头部元素,然后我们发现我们寻找s串的时候下标位置在Str+Str的前半部分,有如下的结果,那么我们就可以得出s1==s3,s2==s1,所以s1==s3==s3,同理也可以得出s2与s3之间的字符串也必然是0个或者多个s1组成的字符串。这样充分性得以说明。
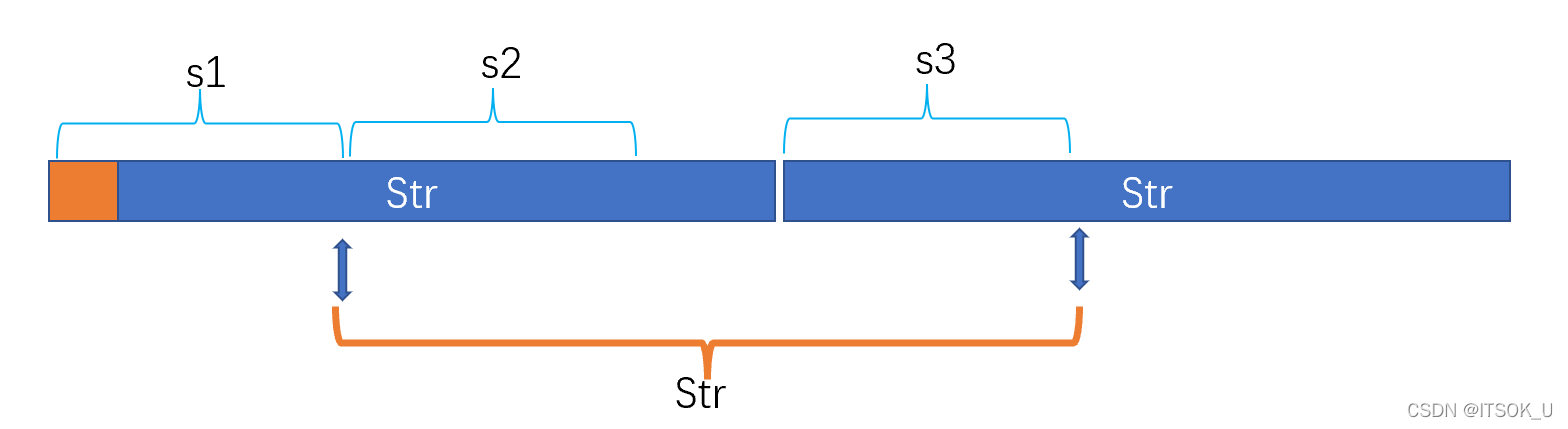
所以,对于字符串Str+Str而言,我们去掉首元素进行查找Str的话,其查找的下标返回值必然会在原本的Str+Str的前半部分。如果是在后半部分也就是下标Str.size()位置,就说明串不是重复的。如下图所示
如果还是不理解可以查看这篇博客再学习一下。
3.题目解答
3.1 穷举法
bool repeatedSubstringPattern(string s) {
int len = s.size();
//枚举子串的长度
for(int i=1;i<=len/2;i++){
bool flag = true;
//可以整除说明满足重复的前提
if(len % i==0){
for(int j=i;j<len;j++){
//如果是重复子串则必会循环
if(s[j]!=s[j-i]){
flag = false;
break;
}
}
if(flag) return true;
}
}
return false;
}
3.2 利用KMP算法解题
class Solution {
public:
//求next数组
void getNext(int *next,const string &s){
next[0]=0;
int j=0;
int len = s.size();
for(int i=1;i<len;i++){
while(j>0 && s[i]!=s[j]){
j=next[j-1];
}
if(s[i]==s[j]) j++;
next[i]=j;
}
}
//将问题转换为一般的求字符串匹配问题
bool repeatedSubstringPattern(string s) {
if(s.size()==0) return false;
int len = s.size();
int next[len];
getNext(next,s);
//
if(next[len-1]!=0 && len%(len-next[len-1])==0){
return true;
}
return false;
}
};
3.3 库函数
bool repeatedSubstringPattern(string s) {
return (s+s).find(s,1)!= s.size();
}
总结:这绝对不是简单题,方法2、3的充分必要性证明有点难
参考资料:
- https://writings.sh/post/algorithm-repeated-string-pattern
- https://programmercarl.com/
- https://leetcode-cn.com/problems/repeated-substring-pattern
