绪论
图的部分自最短路算法的三类算法介绍完毕之后就告一段落了,我们往回看Lecture 18。Lecture 18介绍的是算法思想中重要的一种思想——贪心思想,我当时认为先把图论部分的知识点介绍完全再介绍其他的知识点比较好,但是这个思想在Prim算法,Dijkstra算法(甚至于A*算法)等都有用到,不过课件上对贪心算法的概念介绍的不多,例子又比较抽象(没有直接体现出一个阶段到另一个阶段的扩展),再学习完上述的算法之后体会贪心思想我觉得也是很好的(个人觉得)。
Definition
关于贪心算法首先我们要理解贪心这个词的意义,比如“贪心”是什么?在什么地方“贪心”?为什么要“贪心”?
我们从字面意思上理解“贪心”认为是想要尽可能地获得最优的或者最多的东西,事实上我们现在学习的几乎所有算法都是为了求解某个角度上最优或最多的东西,这样解释“贪心”显然并不准确。
事实上贪心算法的“贪心”从算法表现出来的结果而言更倾向于“短视”:贪心算法适用的问题的任何一个解的求解过程可以分解成若干个阶段,将最后一个解看作一个集合,每个阶段求出这个集合的一个子集,每个阶段求解出来的子集之间可能是前后扩展的关系(Prim算法,Dijkstra算法),也可能是不存在关系的(子阶段对应的子集是最后解的划分而不是前一个阶段子集为后一个阶段子集的子集)。
贪心算法在每个阶段扩展到下一阶段的过程或者处理某个阶段时的问题总是专注于一个“特别的最优解”,并且只扩展该解到下一个阶段的可能,放弃其他所有可能的扩展。
因为不从整体考虑,只对于某个阶段(或者进行到当前的阶段)计算局部的最优解,会有一种不考虑后面影响的感觉,所以我称贪心算法的“贪心”为“短视”,从另一个角度考虑,贪心算法在一个阶段到下一个阶段扩展时放弃了其他所有的可能,只考虑一个“最优解”的情况和扩展,节省了对其他可能扩展花费的时间(这往往能节省很多的时间),又希望这个局部的最优解能够尽可能的接近实际的最优解,这种想法不能说不是“贪心”的(虽然我个人觉得这个greedy并不是我们一般认为的贪婪的意思)。
贪心算法一般按如下步骤进行(括号外是百度百科的内容,括号内是我个人的补充):
1.建立数学模型来描述问题。
2.把求解的问题分成若干个子问题(把求解的问题划分成若干个阶段)。
3.对每个子问题求解,得到子问题的局部最优解(对每个阶段局部最优的解扩展,扩展到下一个阶段,在下一个仅讨论最优解扩展出来的可能)。
4.把子问题的解局部最优解合成原来解问题的一个解(扩展到最后一个阶段得到最优解)。
例如我们的Prim算法,第k个阶段的问题就是求解包含初始点结点个数为k的最小生成树,然后扩展到结点个数为k+1的最小生成树(如果实际推理过Prim算法,会更倾向于从一个阶段下一个阶段扩展的说法,而不是简单的合并,因为阶段之间都是存在关联的)。
Dijkstra算法从一个阶段扩展到下一阶段体现的更加明显,这里就不多作赘述了。
下面是可以使用贪心算法处理的一系列经典问题。
Coin changing
存在若干种数量无限价值不同的硬币,希望你求出表示一个代价最少需要的硬币数(找钱给你的硬币最少)。

就是求解价值V最少能用多少枚硬币表示,朴素的想法是计算出价值V的所有表达方式,选取使用硬币最少的一种(也可以是小于等于V的所有表达方式,这样更符合阶段到阶段的扩展,但在第一次接触这个问题时不容易直接想到,我们在下一个问题中介绍这种想法的推理)。
从我们前面贪心的经验去考虑,选取50币值的硬币表示价值V使用的硬币个数一般要比选取1币值的硬币表示价值V,粗糙的想法是再不超过价值V的情况下尽可能选取币值大的硬币。
于是第i个阶段包含选取前i大的币种能够达到的小于等于V的价值,每个阶段求解前i大的币种能够达到的小于等于V的最大价值,然后以这个最大价值扩展到下一阶段的选取硬币,当进行至多(货币种类数-1)个阶段后,能够得到符合上述贪心思想求解出来的方案。
不过很遗憾的是上面求解出来局部最优解并不完全是实际上的最优解(可以找到反例),它只在部分的币种(欧元和美元都是)下是实际上的最优解。
如果单纯从前一个阶段向后一个阶段扩展的思路来看,能想到的是第i个阶段求解价值i能少能用多少枚硬币表示,可惜的是在这里按照这样设定的按阶段求解,前后两个阶段并不存在很明显的可以扩展的关系(只是前后不满足)。
Interval scheduling
区间调度问题(interval scheduling),换个大家可能更熟悉的名字,就是尽可能选取多个不相交的区间。
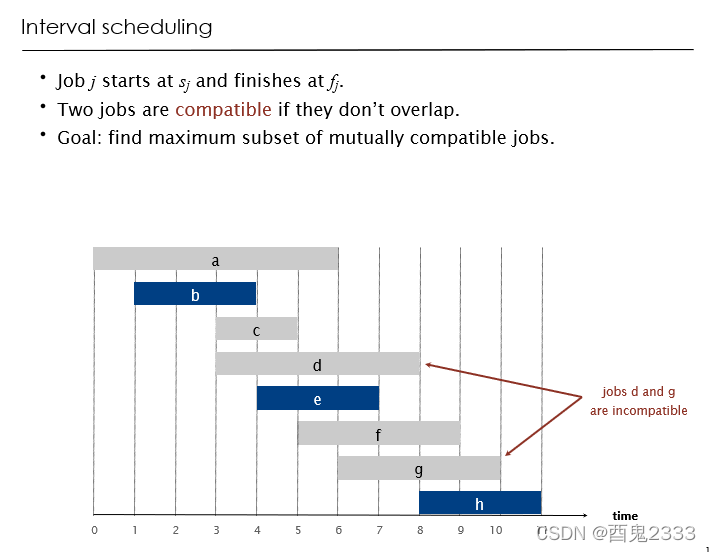
朴素的想法是求解出所有compatible的方案,寻找区间选取个数最多的方案。这里所有compatible的方案和coin changing问题中所有价值小于等于V的表达方式是类似的,所有compatible的方案可以按照选取区间的个数划分成若干个阶段,第i个阶段包含选取i个区间的compatible的方案,可以确定的是第i+1个阶段的某个方案一定是由第i个阶段的某个方案扩展得到的。
但是上述的扩展方向和被扩展的来源都不是固定的,对于一个选取了i+1个区间的方案,它的来源可以是去掉了i+1个区间的任一一个选取了i个区间的方案,同理对于一个选取了i个区间的方案有可能扩展出若干种选取了i+1个区间的方案。
我们固定扩展的方式是在选取了i个区间的方案最右的区间右边选取一个不相交的区间,从选取i个区间的方案扩展到选取i+1个方案,这样扩展的方式也可以保证没有一个方案在扩展的过程中被遗漏(反证法咯hhhh)。
因为每次扩展是在当前已经选取的区间的最右端加入新的区间,我们希望能够尽可能在右端空余的地方加入尽可能多的区间,有显然的结论是右端空余的越多,能够加入的新的区间就越可能的多。这样可以想到的贪心策略是从选取了i个区间的方案到i+1个区间的方案扩展时,尽可能地选取右边节点值小的区间(这里地f表示的就是区间右边的节点值)。

从阶段扩展的角度想,这里贪心算法得到实际最优解是必然的。
Interval partitioning
区间划分,就是多机调度问题,希望我们用尽可能少的机器在一段时间内完成若干个不同时间区间的任务,同一个机器在一个时间只能完成一个任务。
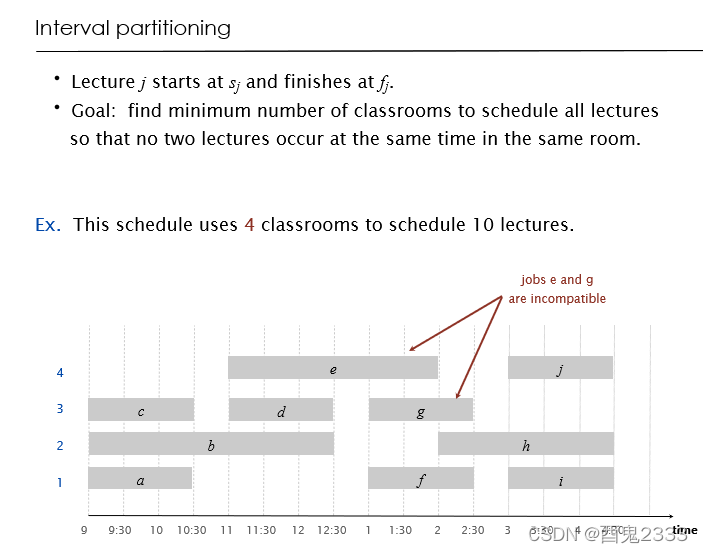
朴素的想法是从小到大的考虑:1个机器是否能完成所有的任务,2个机器是否能完成所有的任务,········对于i个机器能否所有的任务都进行检验。
首先能想到的贪心策略是和前面一样,将任务按照左端点的顺序从小到大排序,然后进行从左到右的扩展。
那么一个一个机器从左到右的扩展还是所有机器一起从左到右的扩展呢?考虑到如果存在k个任务在某个时间点重叠,那么至少需要k个机器,在这种情况下,任何一种方式无法扩展另一种方式也无法进行扩展,但是因为任务是按照左端点的顺序从小到大排序的,一个一个机器的扩展,可能会出现前面个机器选择工作的任务在后面的机器中工作能够节省的更多时间(前面机器的第一个任务左端点小且右端点大,后面机器的第一个任务左端点大右端点小),事实上在现实生活中也是有机器空余就去完成任务,第二种扩展方式更符合现实的逻辑。
我们确定i个机器是同时从左到右进行扩展,这就相当于上一个问题中区间的每个点能够被覆盖i次,我们从小大的考虑变为:能够被覆盖1次的区间能否选取给定的区间,能够被覆盖2次的区间能否选取给定的区间······
考虑能够被覆盖i次的区间能否选取所有的区间到考虑能否被覆盖i+1次的区间能否选取所有的区间不用重新考虑,只需要对覆盖i次的区间进行一次“扩容”,“扩容”到覆盖i+1次的区间即可,因为同时从左到右的扩展,覆盖i次的区间无法选取的区间,在覆盖i+1的区间的任意i个区间也无法选取成功。
流程如下:

从上面的角度来看和前面选取区间的问题是一样的。
Scheduling to minimize lateness
现在有n个任务需要你完成,这里的任务和前面的任务不一样,只告诉你完成需要的时长和希望完成的期限时间,如果没有在期限时间之前完成,实际完成的时间减去预期时间就是这个任务的lateness,所有任务lateness的最大值称为L,希望你能计算出最小的L。
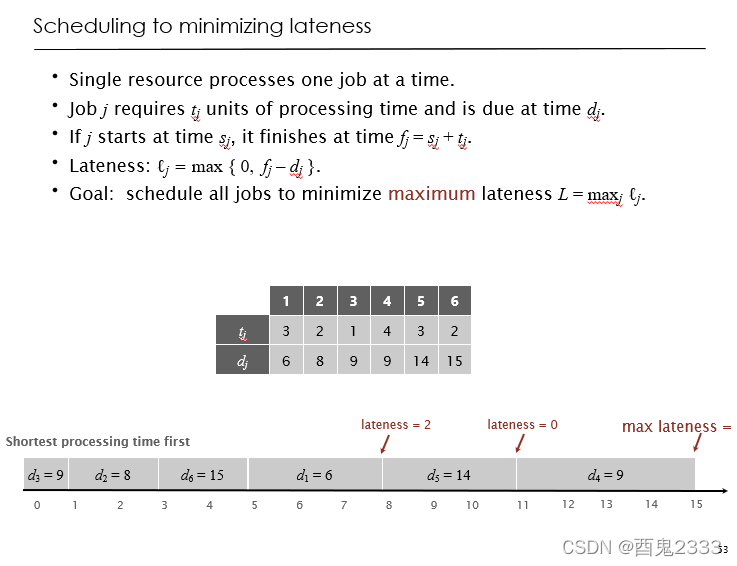
首先由一点可以显然确定,就是这些任务的完成一定是紧接着的,不会出现一个任务完成之后停若干时间再进行下一个任务。这样朴素的做法很容易想到,就是全排列枚举出所有完成任务的顺序,然后计算出最小的L。
和上个问题一样同理我们可以将n个任务的完成看作一个从左到右的扩展,第i个阶段完成i个任务,每个阶段计算出任务选择到当前L的值,第i个阶段扩展到第i+1就是在i个任务的基础上进行第i+1个任务。
前i个任务已经进行了一段时间,对于第i+1个任务不希望它的lateness过大,那么希望该任务的due值尽可能小,那么这个问题的贪心策略又可以得到了,就是每次扩展出当前预期时间最小的任务。

(证明过程考虑存在违反顺序情况的反证法,要具体证明出来还是比较麻烦的)
Optimal offline caching
给定一个缓存可以同时存储k个任务,m个指令每个指令需求一个任务,当进行一个指令时需要指令需求的任务存储在缓存中,将缓存中的任务拿出换一个别的任务的操作称为eviction(驱逐),求最少的驱逐次数。

阶段的划分很简单,将对每个指令进行的操作看作一个阶段(不变化也看做操作),求m个阶段后最少进行eviction操作的方案(朴素想法依旧是列举所有可行的方案)。
那什么时候一定要进行eviction操作呢?如果进行到一个阶段,当前缓存内的任务不能满足指令的需求,那么一定要进行eviction。
那么我们再没有出现必要进行eviction的阶段进行eviction能否降低后面eviction的次数呢?结果是不可能的,我们假设没有必要进行eviction的阶段距离需要进行eviction的第一个阶段k个阶段(k≥1,没有必要进行eviction的阶段在前),这k个阶段一定不会出现需要eviction操作替换之后的任务,但有可能需要eviction操作替换之前的任务,需要eviction操作替换之前的任务会带来更多的eviction操作。
所以初步的贪心策略已经确定:当第i个阶段的存储不满足第i条指令的需求再进行eviction。
那么还有一个问题,替换之后的任务我们可以确定是第i条指令需求的任务,那替换之前的任务呢?我们肯定不希望替换之前的任务在被替换之后后面的指令被立刻用到,所以被替换的任务被需要的阶段应该尽可能地靠后(我尽力了)。
于是有算法框架如下:
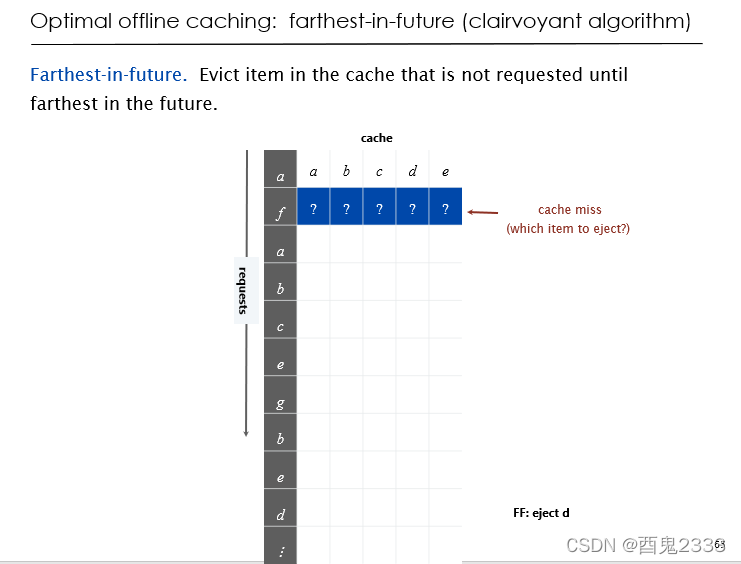
这个算法适用于我们对所有的指令已知,所以算法作用的背景为optimal(最优的) offline(离线的)。
总结
我们这章节讨论了贪心算法的思想,框架和经典案例。我没有过多的讨论贪心算法的背景(贪心选择性质,最优子结构性质),因为最优子结构性质不是贪心算法独有的背景,而贪心策略得到的解往往是一个局部最优解而不是整体最优解(我们往往只需要局部最优解而不需要整体最优解),强行记忆背景而不自己去探究框架并不是很好的做法。
框架是先考虑问题的朴素处理方法(暴力方法),将朴素的处理方法划分成若干个阶段,然后考虑阶段与阶段前后之间存在怎样的扩展关系(贪心算法一般都是前后两个阶段扩展),然后根据观察得到的“经验”指定策略来减少扩展的方向(阶段的求解)的可能,或者两者同时进行。
也就是说对于一个良好的贪心算法的设计,阶段扩展过程,问题朴素算法设计的认识和阶段求解过程经验的提取同时需要,同样重要,甚至前后存在一定的启发关系(从朴素算法的设计,阶段的划分的基础上提取贪心策略的经验)。
至于贪心策略得到的局部最优解是否是实际最优解往往需要很大的精力和良好的数学基础去证明,由于我们现在往往只是需要局部最优解,所以我找到另一个课件上的一段话来安慰无法证明的大家(也许只有我hhhh)。

