欢迎关注更多精彩
关注我,学习常用算法与数据结构,一题多解,降维打击。
曲率计算中的变量
领域面积计算
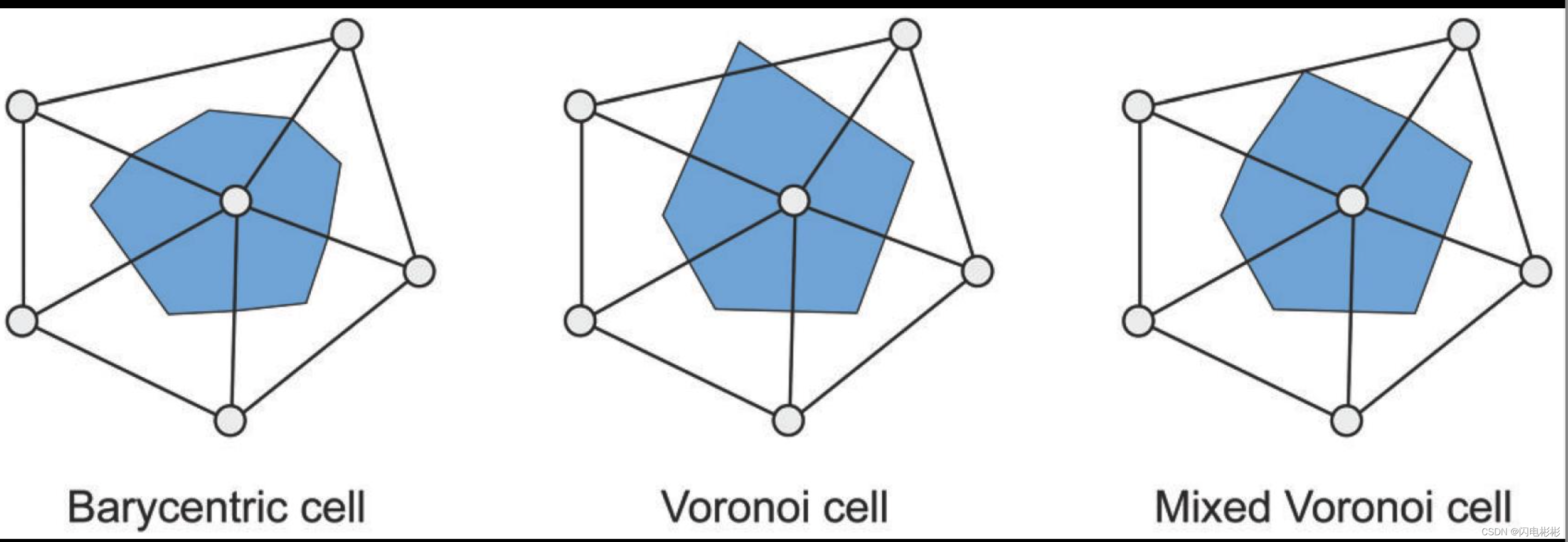
领域面积计算有三种形式
- 中点法,即取边的中点和三角形的中连线后形成的多边形区域。
- 泰森多边法,对每条1邻域边作中垂线,形成的多边形区域。
- 混合法,默认用方法2,当三角形是钝角三角形时,泰森多边法形成的区域会越界,此时,越界的三角形的中心点用钝角对边的中点代替。
绝对平均曲率
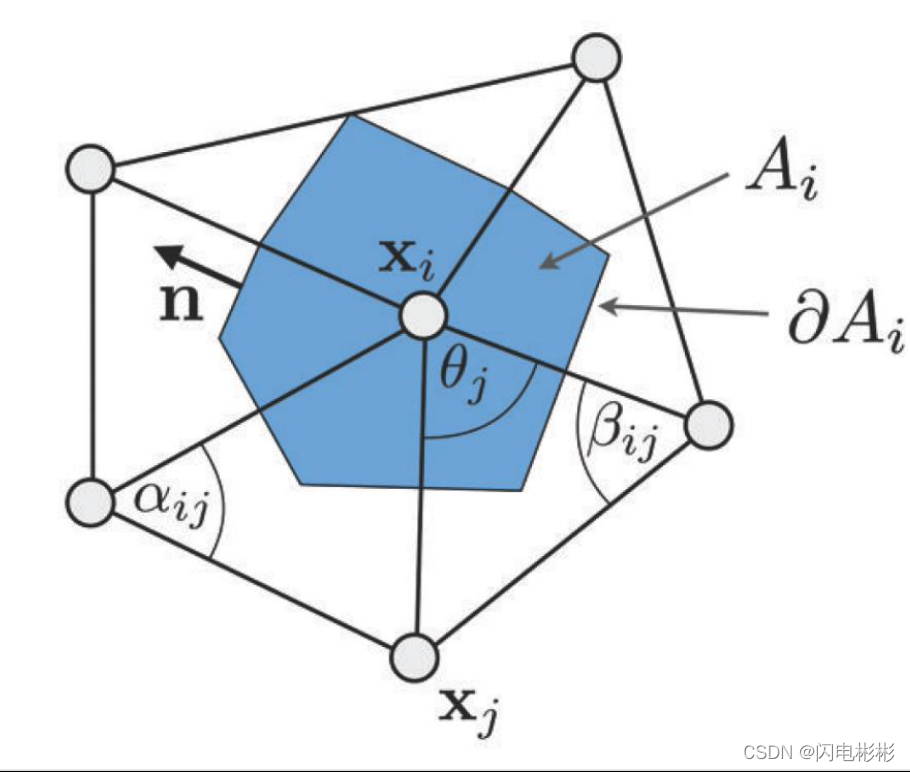
x
i
是
第
i
个
点
x_i 是第i个点
xi?是第i个点
A i 是 x i 1 邻 域 面 积 A_i是x_i1邻域面积 Ai?是xi?1邻域面积
x i 拉 普 公 式 为 Δ x i = 1 2 A i ∑ j ∈ Ω ( i ) ( cot ? α i j + cot ? β i j ) ( x j ? x i ) ) x_i拉普公式为\Delta{x_i}=\frac {1}{2A_i} \displaystyle \sum_{j\in \Omega(i)}(\cot \alpha_{ij} + \cot \beta_{ij})(x_j-x_i)) xi?拉普公式为Δxi?=2Ai?1?j∈Ω(i)∑?(cotαij?+cotβij?)(xj??xi?))
由于,cotx = 1/tanx,所以
Δ x i = 1 2 A i ∑ j ∈ Ω ( i ) ( 1 tan ? α i j + 1 tan ? β i j ) ( x j ? x i ) \Delta{x_i}=\frac {1}{2A_i} \displaystyle \sum_{j\in \Omega(i)}(\frac {1}{\tan \alpha_{ij}} + \frac {1}{\tan \beta_{ij}})(x_j-x_i) Δxi?=2Ai?1?j∈Ω(i)∑?(tanαij?1?+tanβij?1?)(xj??xi?)
绝 对 平 均 曲 率 H i = 1 2 ∣ ∣ Δ x i ∣ ∣ = 1 4 A i ∑ j ∈ Ω ( i ) ( 1 tan ? α i j + 1 tan ? β i j ) ( x j ? x i ) 绝对平均曲率H_i = \frac 1 2 ||\Delta x_i|| = \frac {1}{4A_i} \displaystyle \sum_{j\in \Omega(i)}(\frac {1}{\tan \alpha_{ij}} + \frac {1}{\tan \beta_{ij}})(x_j-x_i) 绝对平均曲率Hi?=21?∣∣Δxi?∣∣=4Ai?1?j∈Ω(i)∑?(tanαij?1?+tanβij?1?)(xj??xi?)
计算代码
github: https://github.com/LightningBilly/ACMAlgorithms/tree/master/图形学算法/三角网格算法/曲率可视化/
核心计算代码
MVector3 cal_circum_enter(const MVector3& a, const MVector3& b, const MVector3& c)
{
MVector3 ac = c - a, ab = b - a;
MVector3 abXac = cross(ab, ac), abXacXab = cross(abXac, ab), acXabXac = cross(ac, abXac);
return a + (abXacXab * ac.normSq() + acXabXac * ab.normSq()) / (2.0 * abXac.normSq());
}
// 计算邻域面积
void cal_local_ave_region(PolyMesh* const mesh, std::vector<double> &vertexLAR)
{
vertexLAR.assign(mesh->numVertices(), 0);
for(auto v:mesh->vertices()) {
auto ps = mesh->vertAdjacentPolygon(v);
if(ps.size()==0)continue;
auto n = ps[0]->normal();
for(int i=1;i<ps.size();i++) n+=ps[i]->normal();
n/=ps.size();
v->setNormal(n); // 更新点的normal
}
for (MPolyFace* fh : mesh->polyfaces())
{
// judge if it's obtuse
bool isObtuseAngle = false; // 是否为钝角三角形
MVert *obtuseVertexHandle;
MHalfedge *he = fh->halfEdge();
MHalfedge *he_next = he->next(), *he_prev = he->prev();
MVert *v_from_he = he->fromVertex(), *v_from_he_next = he_next->fromVertex(), *v_from_he_prev = he_prev->fromVertex();
MVector3 vec_he_nor = he->tangent(), vec_he_next_nor = he_next->tangent(), vec_he_prev_nor = he_prev->tangent();
if (vectorAngle(vec_he_nor, -vec_he_prev_nor) > M_PI / 2.0)
{
isObtuseAngle = true;
obtuseVertexHandle = v_from_he;
}
else if (vectorAngle(vec_he_next_nor, -vec_he_nor) > M_PI / 2.0)
{
isObtuseAngle = true;
obtuseVertexHandle = v_from_he_next;
}
else if (vectorAngle(vec_he_prev_nor, -vec_he_next_nor) > M_PI / 2.0)
{
isObtuseAngle = true;
obtuseVertexHandle = v_from_he_prev;
}
// calculate area
if (isObtuseAngle)
{ // 是钝角要采用中点法算面积
double faceArea = 0.5*norm(cross(v_from_he_next->position() - v_from_he->position(), v_from_he_prev->position() - v_from_he->position()));
for (MVert* fv : mesh->polygonVertices(fh))
{
if (fv == obtuseVertexHandle)
vertexLAR[fv->index()] += faceArea / 2.0;
else
vertexLAR[fv->index()] += faceArea / 4.0;
}
}
else
{ // 普通的采用泰森多边形法算面积
MVector3 cc = cal_circum_enter(v_from_he->position(), v_from_he_next->position(), v_from_he_prev->position());
for (MHalfedge* fhh : mesh->polygonHalfedges(fh))
{
MVector3 edgeMidpoint = 0.5*(fhh->fromVertex()->position() + fhh->toVertex()->position());
double edgeLength = fhh->edge()->length();
double partArea = 0.5 * edgeLength * (edgeMidpoint - cc).norm();
vertexLAR[fhh->fromVertex()->index()] += 0.5*partArea;
vertexLAR[fhh->toVertex()->index()] += 0.5*partArea;
}
}
}
}
void cal_mean_curvature(PolyMesh* const mesh, const std::vector<double> &vertexLAR, std::vector<double> &meanCur, std::vector<double> &absMeanCur)
{
meanCur.assign(mesh->numVertices(), 0);
absMeanCur.assign(mesh->numVertices(), 0);
for (MVert* vh : mesh->vertices())
{
MVector3 p_temp = { 0.0,0.0,0.0 }, p_vh = vh->position();
for (auto voh_it = mesh->voh_iter(vh); voh_it.isValid(); ++voh_it)
{
if (!(*voh_it)->isBoundary())
{
MHalfedge* next_voh = (*voh_it)->next();
MVert* to_voh = (*voh_it)->toVertex(), *to_next_voh = next_voh->toVertex();
MVector3 p_to_voh = to_voh->position(), p_to_next_voh = to_next_voh->position();
double angle_voh = vectorAngle(p_vh - p_to_voh, p_to_next_voh - p_to_voh),
angle_next_voh = vectorAngle(p_to_voh - p_to_next_voh, p_vh - p_to_next_voh);
p_temp += (p_to_next_voh - p_vh) / tan(angle_voh);
p_temp += (p_to_voh - p_vh) / tan(angle_next_voh); // 利用cot拉普拉斯算子算出绝对平均曲率
}
}
p_temp /= 4 * vertexLAR[vh->index()];
if (dot(p_temp, vh->normal()) > 0) // 判断与点法向关系决定曲率符号
meanCur[vh->index()] = -p_temp.norm();
else
meanCur[vh->index()] = p_temp.norm();
absMeanCur[vh->index()] = p_temp.norm();
}
std::cout << "Calculate Mean Curvature Done" << std::endl;
std::cout << "Calculate Absolute Mean Curvature Done" << std::endl;
}
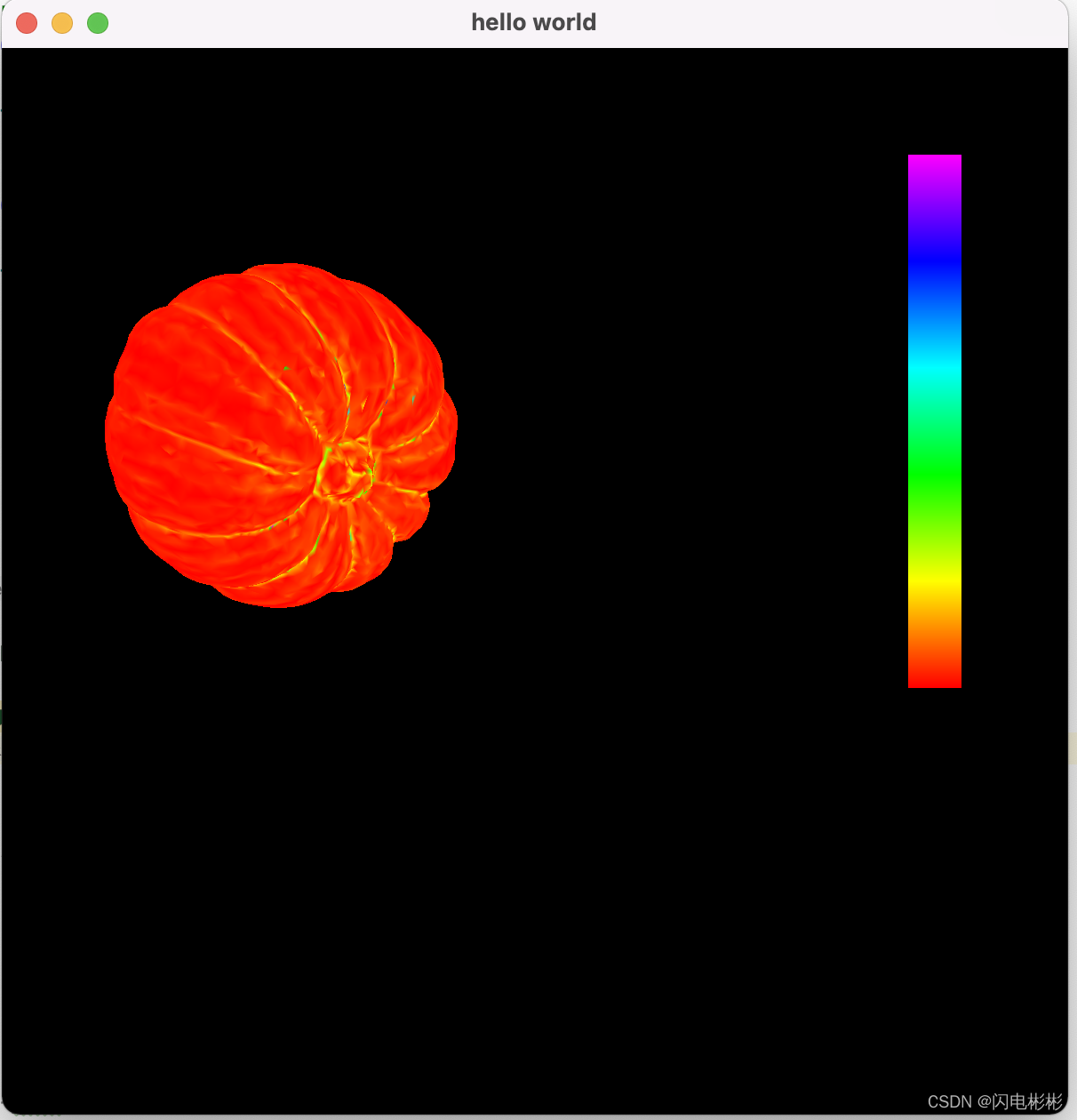
效果展示
南瓜
牛

本人码农,希望通过自己的分享,让大家更容易学懂计算机知识。

