797. 所有可能的路径
难度 中等
给你一个有 n 个节点的 有向无环图(DAG),请你找出所有从节点 0 到节点 n-1 的路径并输出(不要求按特定顺序)
graph[i] 是一个从节点 i 可以访问的所有节点的列表(即从节点 i 到节点 graph[i][j]存在一条有向边)。
示例 1:
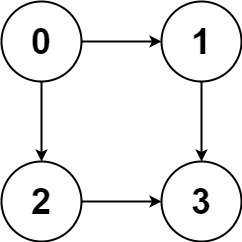
输入:graph = [[1,2],[3],[3],[]]
输出:[[0,1,3],[0,2,3]]
解释:有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3
示例 2:
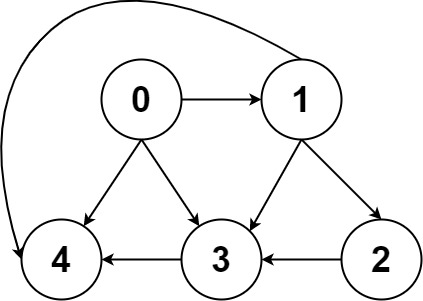
输入:graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出:[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
提示:
n == graph.length2 <= n <= 150 <= graph[i][j] < ngraph[i][j] != i(即不存在自环)graph[i]中的所有元素 互不相同- 保证输入为 有向无环图(DAG)
题解
? 这道题是道图的题目,而且给出了说明是有向无环图(DAG),那我们就直接考虑深搜模板就行了,访问标记数组也不用设置,因为一定不会访问到已经搜索到的节点。每次搜索到一个新的节点就把这个节点相邻的节点进行扩展,然后如果扩展的节点是第n-1个节点,就找到一条从0通往n-1节点的路径。
class Solution {
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
List<List<Integer>> ans = new ArrayList<List<Integer>>();//结果列表
int n = graph.length - 1;//第n-1个节点
Deque<Integer> queue = new ArrayDeque<>(n);//新建一个n个元素的数组
queue.addLast(0);//从0开始
for(int i = 0; i < graph[0].length; i++){//遍历0的相邻节点
queue.addLast(graph[0][i]);//相邻节点入队
dfs(graph[0][i], n, graph, queue, ans);//深搜相邻节点
queue.removeLast();//出队
}
return ans;
}
void dfs(int k, int n, int[][] graph, Deque<Integer> queue, List<List<Integer>> ans){
if(k == n){//找到第n-1个节点
ans.add(new ArrayList<Integer>(queue));//存储答案
return;
}
for(int i = 0; i < graph[k].length; i++){//遍历第k个节点的相邻节点
queue.addLast(graph[k][i]);//相邻节点入队
dfs(graph[k][i], n, graph, queue, ans);//深搜相邻节点
queue.removeLast();//出队
}
}
}
