[数据结构与算法]【JZ46 把数字翻译成字符串】

描述

有一种将字母编码成数字的方式：'a'->1, 'b->2', ... , 'z->26'。
我们把一个字符串编码成一串数字，再考虑逆向编译成字符串。
由于没有分隔符，数字编码成字母可能有多种编译结果，例如 11 既可以看做是两个 'a' 也可以看做是一个 'k' 。但 10 只可能是 'j' ，因为 0 不能编译成任何结果。
现在给一串数字，返回有多少种可能的译码结果

数据范围：字符串长度满足 0 < n ≤ 90
进阶：空间复杂度 O(n)，时间复杂度 O(n)

示例1

输入： "12"

返回值：2

说明：2种可能的译码结果（”ab” 或”l”）    

示例2

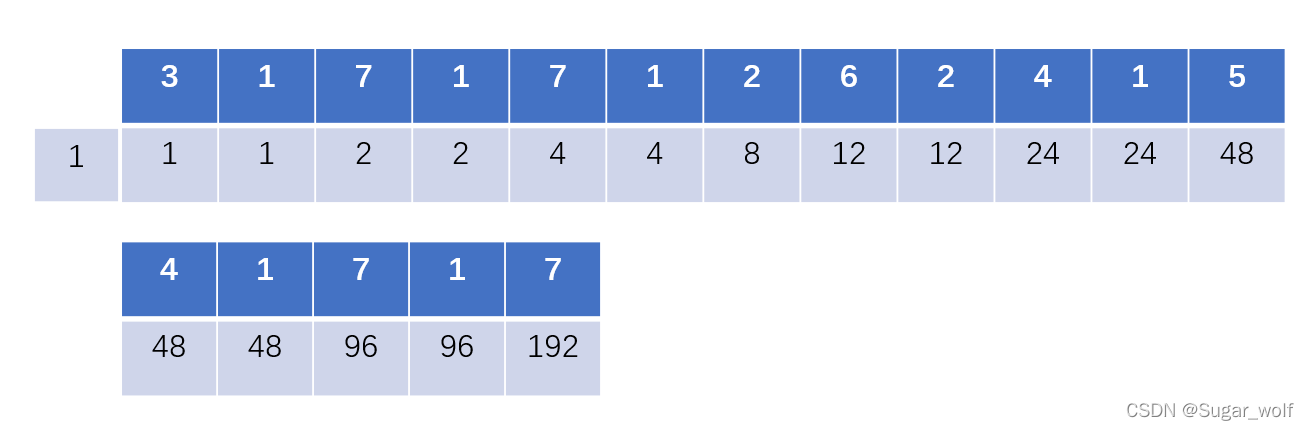
输入： "31717126241541717"

返回值：192

说明：192种可能的译码结果 

分析：

1. 首先对数据进行分类，对于空字符串、首字符为‘0’的字符串，以及‘0’的前一位不是‘1’或者‘2’的字符串，输出0；

2. 建立一个动态数组dp[len+1],用于存储有几种译码结果。dp[0]=1,dp[1]=1。

   1）若第k个字符和第 k-1 个字符能够组合成a到z的合法字符，则dp[k+1]=dp[k]+dp[k-1];

   2）若无法组成合法字符，则译码结果没有增加，dp[k+1]=dp[k];

   3）若第k个字符和第 k-1 个字符中有 ‘0’，则无法产生新的译码方式，dp[k+1]=dp[k];

代码：

class Solution {
    public:
    int solve(string nums) {
        int len = nums.size();
        if (len == 0)
            return 0;
        for (int k = 0;k < len;k++)
        {
            if (nums[k]=='0')
            {
                if (k == 0)
                    return 0;
                else if (nums[k-1] != '1' && nums[k-1] != '2')
                    return 0;
            }
        }//如果0位于第一位或者0的前面不是1或者2，则无法进行译码
        int dp[len+1],temp;
        dp[0] = 1;
        dp[1] = 1;
        for (int k=1;k<len;k++)
        {
            temp=(nums[k]-'0')+(nums[k-1]-'0')*10;
            if (temp > 0 && temp <= 26 && nums[k]!= '0'&& nums[k-1] != '0')
                dp[k+1] = dp[k]+dp[k-1];
            else
                dp[k+1] = dp[k];
        }
        return dp[len];
    }
};

运行时间：6ms
超过15.56% 用C++提交的代码
占用内存：424KB
超过46.36%用C++提交的代码

阅读世界，共赴山海

423全民读书节，邀你共读