题目要求

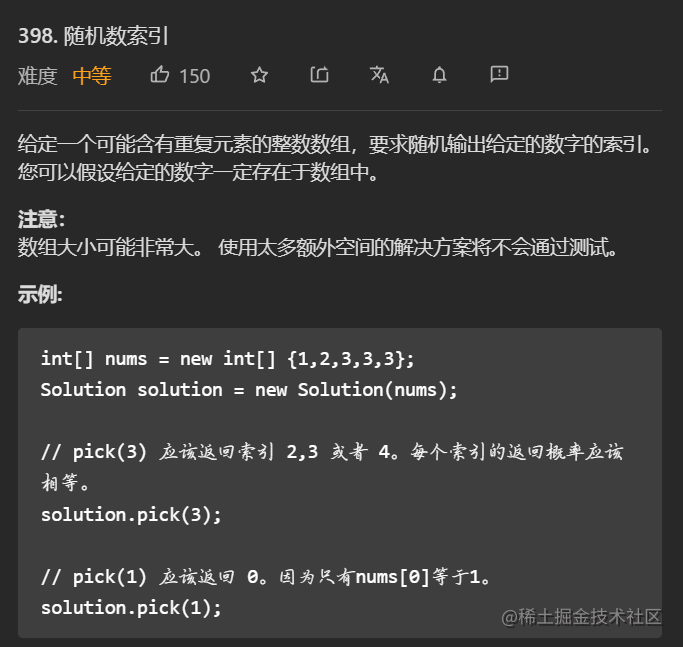
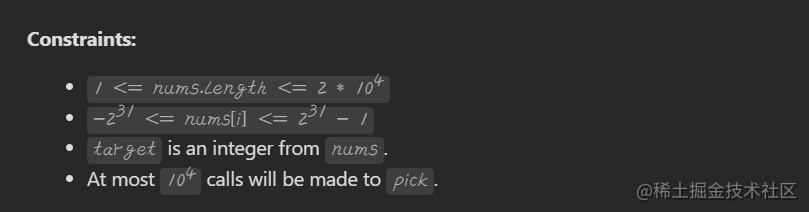
思路一：模拟、哈希表

把数组内容整理一下放哈希表，然后从哈希表取值随机返回。
哈希表存的内容是数组元素和它对应的所有下标。

Java

class Solution {
    Map<Integer, List<Integer>> map;
    Random ran;

    public Solution(int[] nums) {
        map = new HashMap<Integer, List<Integer>>();
        ran = new Random();
        for(int i = 0; i < nums.length; ++i) {
            map.putIfAbsent(nums[i], new ArrayList<Integer>()); // 相同元素放一起
            map.get(nums[i]).add(i); // 存下标
        }
    }
    
    public int pick(int target) {
        List<Integer>idx = map.get(target); // 取下标
        return idx.get(ran.nextInt(idx.size()));
    }
}

时间复杂度：初始化为 $O (n)$ ，pick函数为 $O (1)$
空间复杂度： $O (n)$

C++

class Solution {
    unordered_map<int, vector<int>> map;
public:
    Solution(vector<int>& nums) {
        for(int i = 0; i < nums.size(); ++i)
            map[nums[i]].push_back(i); // 相同元素下标放一起
    }
    
    int pick(int target) {
        auto &idx = map[target]; // 取下标
        return idx[rand() % idx.size()];
    }
};

时间复杂度：初始化为 $O (n)$ ，pick函数为 $O (1)$
空间复杂度： $O (n)$

思路二：水塘抽样（蓄水池抽样）

降低空间复杂度，边读边取，适用于长长长文件读取处理。

遍历 $n u m s$ ，每次遇到 $t a r g e t$ 元素都选择性更新结果。
设当前为第 $c n t$ 次，选择方法为产生 $[0, c n t)$ 内的一个随机整数 $r a n$ ：
- 若 $r a n = 0$ ，更新结果为当前元素在数组中的下标（不是 $c n t$ ）；
- 若 $ran\ne 0$ ：不更新结果。

这个选择方法是怎么保证返回每个下标概率相同的呢？
$\quad P(第i个target元素下标成为结果)$
$\quad P(ran_i=0)\times P(ran_{i+1}\ne 0)\times \dots\times P(ran_k\ne 0)$
$=\frac{1}{i}\times(1-\frac{1}{i+1})\times\dots\times(1-\frac{1}{k})$
$=\frac{1}{i}\times\frac{i}{i+1}\times\dots\times\frac{k-1}{k}$
$=\frac{1}{k}$
注： $ran_i$ 指第 $i$ 轮中选择的随机数。

Java

class Solution {
    int[] nums;
    Random ran;

    public Solution(int[] nums) {
        this.nums = nums;
        ran = new Random();
    }
    
    public int pick(int target) {
        int res = 0;
        for(int i = 0, cnt = 0; i < nums.length; ++i) {
            if(nums[i] == target) {
                ++cnt; // 第cnt个target
                if(ran.nextInt(cnt) == 0)
                    res = i;
            }
        }
        return res;
    }
}

时间复杂度：初始化为 $O (1)$ ，pick函数为 $O (n)$
空间复杂度： $O (1)$

C++

class Solution {
    vector<int> &nums;
public:
    Solution(vector<int>& nums) : nums(nums) {}
    
    int pick(int target) {
        int res;
        for(int i = 0, cnt = 0; i < nums.size(); ++i) {
            if(nums[i] == target) {
                ++cnt; // 第cnt个target
                if(rand() % cnt == 0)
                    res = i;
            }
        }
        return res;
    }
};