This arctile covers:
- Introducing support vector machines
- Using the SMO(sequential minimal optimization?序列最小优化算法(英语:Sequential minimal optimization, SMO)是一种用于解决支持向量机训练过程中所产生优化问题的算法。目前被广泛使用于SVM的训练过程中,并在通行的SVM库LIBSVM中得到实现.) algorithm for optimization?
- Using kernels to "transform"
- Comparing support vector machines with other classifers
Support vector machines are considered by some people to be the best stock classifier.Support vector machines make good decisions for data points that are outside the training set.
In this arctile , we're going to learn
- what support vector machines are.
- Introducing some key terminology. The sequential minimal optimization(SMO) algorithm.
- How to use something called kernels to extend SVMs to a larger number of datasets.
- revisit the handwriting example from chapter 1 to see if we can do a better job with SVMs.
6.1 Separating data with the maximum margin
Support vector machines
Pros:
- Low generalization error?
- computationally inexpensive
- easy to interpret results
Cons:
- Sensitive to tuning parameters and kernel choice
- natively only handles binary classification
Works with:?
- Numeric values
- nominal values

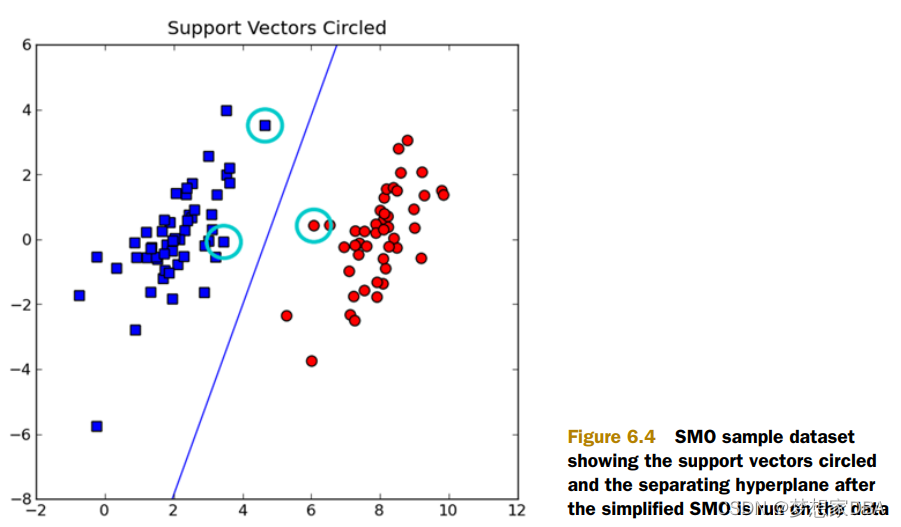
There are two groups of data,and the data points are separated enough that you could draw a straight line on the figure with all the points of one class on ons side of the line and the points of the other class on the other side of the line. this data is linealy separable. The line used to separate the dataset is called separating hyperplane.?
The points closet to the separating hyperplane are known as support vectors.
?6.2 Finding the maximum margin
How can we measure the line best separates the data?

6.2.1 Framing the optimization problem in terms of our classifier
?Understanding how the classifier works will help you to understand the optimization problem. We'll have a simple equation like the sigmod where we can enter our data values and get a class label out.

?
6.2.2 Approaching SVM with our general framework
General approach to SVMs
1. Collect: Any method.
2. Prepare: Numeric values are needed.
3. Analyze: It helps to visualize the separating hyperplane.
4. Train: The majority of the time will be spent here. Two parameters can be adjusted during this phase.
5. Test: Very simple calculation.
6. Use: You can use an SVM in almost any classification problem. One thing to note is that SVMs are binary classifiers. You’ll need to write a little more code to use an SVM on a problem with more than two classes.
6.3 Efficient optimization with the SMO algortihm
A quadratic solver is a piece of software that optimizes a quadratic function of several variables,subject to linear constraints on the variables.
6.3.1 Platt's SMO algortithm
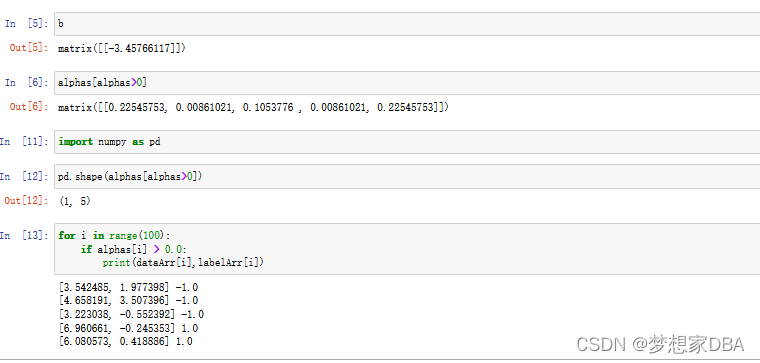
The SMO algorithm works to find a set of alphas and b. Once we have a set of alphas, we can easily compute our weights w and get the separating hyperplane.
6.3.2 Soving small datasets with the simplified SMO
import random
def loadDataSet(fileName):
dataMat = [];labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]),float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
def selectJrand(i,m):
j = i
while (j==i):
j = int(random.uniform(0,m))
return j
def cliAlpha(aj,H,L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj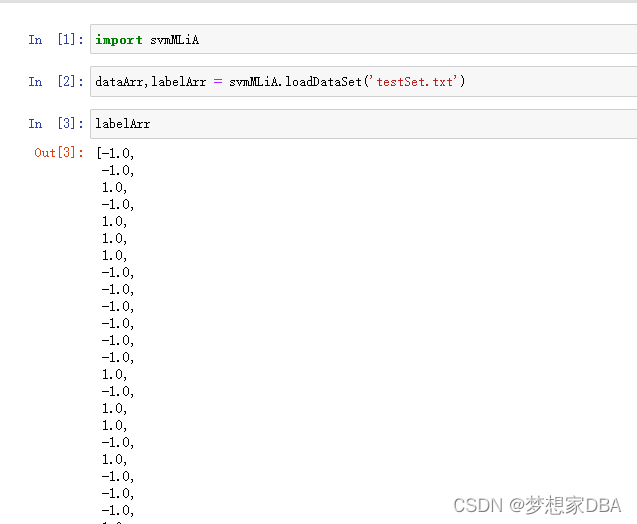
?
# The simplified SMO algorithm
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
# the dataset, the class labels, a constrant C , the tolerance,
# and the maximum number of iteration before quitting
dataMatrix = pd.mat(dataMatIn);labelMat = pd.mat(classLabels).transpose()
b = 0; m,n = pd.shape(dataMatrix)
alphas = pd.mat(pd.zeros((m,1)))
iter = 0
while (iter < maxIter):
alphaPairsChanged = 0
for i in range(m):
fxi = float(pd.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
Ei = fxi - float(labelMat[i])
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
j = selectJrand(i,m)
fxj = float(pd.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
Ej = fxj -float(labelMat[j])
alphaIold = alphas[i].copy();
alphaJold = alphas[j].copy();
if (labelMat[i] != labelMat[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C+alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C,C + alphas[j] + alphas[i])
if L==H:
print("L==H");
continue
eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
if eta >= 0:
print("eta>=0");
continue
alphas[j] -= labelMat[j]*(Ei - Ej)/eta
alphas[j] = cliAlpha(alphas[j],H,L)
if (abs(alphas[j] - alphaJold) < 0.00001):
print("j not moving enough");
continue
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
b1 = b - Ei -labelMat[i]*(alphas[i] - alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
b2 = b - Ej -labelMat[i]*(alphas[i] - alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
if (0 < alphas[i]) and (C > alphas[i]):
b = b1
elif (0 < alphas[j]) and (C > alphas[j]):
b = b2
else:
b = (b1 + b2)/2.0
alphaPairsChanged += 1
print("iter: %d i: %d, pairs changed %d" %(iter,i,alphaPairsChanged))
if (alphaPairsChanged == 0):
iter += 1
else:
iter = 0
print("iteration number: %d" % iter)
return b,alphas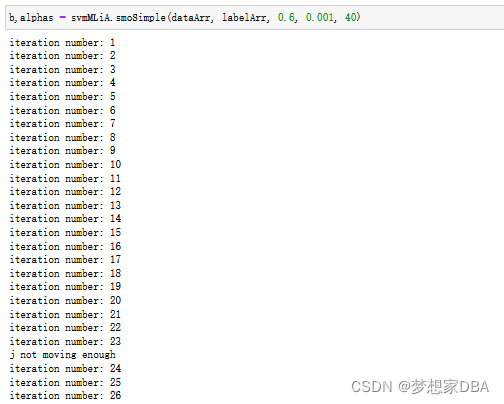
?
?6.4 Speeding up optimization with full Platt SMO
This simplified SMO works OK on small datasets with a few hundred points but slows down? on larger datasets.
The Platt SMO algorithm has an outer loop for choosing the first alpha. This alternates between single passes over the entire dataset and single passes over non-bound alphas.
The second alpha is chosen using an inner loop after we've selected the first alpha.
'''
Author: Maxwell Pan
Date: 2022-04-21 12:07:54
LastEditTime: 2022-04-25 09:41:21
FilePath: \cp06\svmMLiA.py
Description:
Software:VSCode,env:
'''
# Helper functions for the SMO algorithm
import random
import numpy as np
from time import sleep
import matplotlib.pyplot as plt
# input file data
def loadDataSet(fileName):
# data Matrix
dataMat = []
# label vector
labelMat = []
# open file
fr = open(fileName)
# read line gradually
for line in fr.readlines():
# 去掉每一行首尾的空白符,例如'\n','\r','\t',' '
# 将每一行内容根据'\t'符进行切片
lineArr = line.strip().split('\t')
# 添加数据(100个元素排成一行)
dataMat.append([float(lineArr[0]),float(lineArr[1])])
# 添加标签(100个元素排成一行)
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
# m为alpha参数个数,i - alpha ,随机输出与i不通过的j
def selectJrand(i,m):
j = i
while (j==i):
# uniform() 方法将随机生成一个实数,它在[x,y]范围内
j = int(random.uniform(0,m))
return j
"""
函数说明:修剪alpha
Parameters:
aj - alpha值
H - alpha 上限
L - alpha 下限
Returns:
aj - alpha值
Modify:
2022-04-23
"""
def cliAlpha(aj, H, L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
# The simplified SMO algorithm
"""
函数说明: 简化版SMO 算法
Parameters:
dataNatIn - 数据矩阵
classLabels - 数据标签
C - 松弛变量
toler - 容错率
maxIter - 最大迭代次数
Returns:
None
Modify:
2022-04-23
"""
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
# the dataset, the class labels, a constant C , the tolerance,
# and the maximum number of iteration before quitting
dataMatrix = np.mat(dataMatIn);labelMat = np.mat(classLabels).transpose()
b = 0; m,n = np.shape(dataMatrix)
alphas = np.mat(np.zeros((m,1)))
iter = 0
while (iter < maxIter):
alphaPairsChanged = 0 # alphaPairsChanged 是否已进行优化
for i in range(m):
# 即公式为f(xi) = ∑alpha_mi*y_mi*x_mi*xi.T + b 可理解为距离 f(x)为m维行向量
fxi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
Ei = fxi - float(labelMat[i]) # 计算偏差
# 判断条件:正负间隔均判断,同时检查alpha值,保证其不等于C或者0
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
j = selectJrand(i,m) #取不同于i的j
fxj = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
Ej = fxj -float(labelMat[j])
alphaIold = alphas[i].copy()
alphaJold = alphas[j].copy()
# 计算L、H,即alpha_j的上下界
if (labelMat[i] != labelMat[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C+alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C,C + alphas[j] + alphas[i])
if L==H:
#print("L==H");
continue
# η=-(K11+K22?2K12)也可去掉负号,但相应更新alpha_j时累减改成累加
eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
if eta >= 0:
#print("eta>=0");
continue
# 更新alpha_j
alphas[j] -= labelMat[j]*(Ei - Ej)/eta
alphas[j] = cliAlpha(alphas[j],H,L)
if (abs(alphas[j] - alphaJold) < 0.00001):
print("j not moving enough");
continue
# 更新alpha_i
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
# 更新阈值b
b1 = b - Ei -labelMat[i]*(alphas[i] - alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
b2 = b - Ej -labelMat[i]*(alphas[i] - alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
if (0 < alphas[i]) and (C > alphas[i]):
b = b1
elif (0 < alphas[j]) and (C > alphas[j]):
b = b2
else:
b = (b1 + b2)/2.0
alphaPairsChanged += 1
# print("iter: %d i: %d, pairs changed %d" %(iter,i,alphaPairsChanged))
if (alphaPairsChanged == 0):
iter += 1
else:
iter = 0
# print("iteration number: %d" % iter)
return b,alphas
# Support functions for full Platt SMO
# 1. 构建一个数据结构存储所有数据
class optStruct:
def __init__(self,dataMatIn, classLabels, C, toler):
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.m = np.shape(dataMatIn)[0]
self.alphas = np.mat(np.zeros((self.m,1)))
self.b = 0
self.eCache = np.mat(np.zeros((self.m,2))) # Error cache # 误差缓存 第一列是eCache是否有效的标志位,第二列是实际E值
# 2. 计算k处误差值
def calcEk(oS, k):
fXk = float(np.multiply(oS.alphas,oS.labelMat).T*(oS.X*oS.X[k,:].T)) + oS.b
Ek = fXk - float(oS.labelMat[k])
return Ek
# 3. 用于选择第二个α
def selectJ(i, oS, Ei):
maxK = -1;maxDeltaE = 0; Ej = 0 # Inner-loop heuristic
oS.eCache[i] = [1, Ei]
validEcacheList = np.nonzero(oS.eCache[:,0].A)[0] # nonzero 返回数组中非零元素的索引值
if(len(validEcacheList)) > 1:
# 遍历一遍上列表,找出最大差值的Ej
for k in validEcacheList:
if k == i:
continue
Ek = calcEk(oS,k)
deltaE = abs(Ei - Ek)
if(deltaE > maxDeltaE):
maxK = k;
maxDeltaE = deltaE; # Choose j for maximum step size
Ej = Ek
return maxK,Ej
else:
# 第一次,直接随机寻找一个Ej
j = selectJrand(i,oS.m)
Ej = calcEk(oS, j)
return j, Ej
# 4. 计算k处误差值 并存入eCache中
def updateEk(oS, k):#after any alpha has changed update the new value in the cache
Ek = calcEk(oS, k)
oS.eCache[k] = [1,Ek]
# Full Platt SMO optimization routine
# 5. 内部循环,找到配对Ej,则返回1,
"""
函数说明:优化的SMO算法
Parameters:
i - 标号为i的数据的索引值
oS - 数据结构
Returns:
1 - 有任意一对 alpha值发生变化
0 - 没有任意一对alpha值发生变化或变化太小
"""
def innerL(i, oS):
# 步骤1: 计算误差Ei
Ei = calcEk(oS, i)
# 优化alpha,设定一定的容错率
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
# 使用内循环启发方式2 选择alpha_j,并计算Ej
j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
# 保存更新前的alpha值,使用深层拷贝
alphaIold = oS.alphas[i].copy()
alphaJold = oS.alphas[j].copy()
# 步骤2 : 计算上下界H和下界L
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L==H:
print("L==H");
return 0
# 步骤3:计算eta
eta = 2.0 * oS.X[i, :] * oS.X[j, :].T - oS.X[i, :] * oS.X[i, :].T - oS.X[j, :] * oS.X[j, :].T
if eta >= 0:
print("eta>=0")
return 0
# 步骤4:更新alpha_i
oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
# 步骤5:修剪alpha_j
oS.alphas[j] = cliAlpha(oS.alphas[j],H,L)
# 更新Ej至误差缓存
updateEk(oS, j) #added this for the Ecache
if (abs(oS.alphas[j] - alphaJold) < 0.00001):
print("j not moving enough")
return 0
# 步骤6:更新alpha_i
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
# 更新Ei至误差缓存
updateEk(oS, i) #added this for the Ecache #the update is in the oppostie direction
# 步骤7:更新b_1 和 b_2:
b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[i, :].T - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.X[j, :] * oS.X[i, :].T
b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[j, :].T - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.X[j, :] * oS.X[j, :].T
#步骤8:根据b_1 和b_2更新b
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):
oS.b = b2
else:
oS.b = (b1 + b2)/2.0
return 1
else:
return 0
# Full Platt SMO outer loop
"""
函数说明: 完整的线性SMO算法
Parameters:
dataMatIn - 数据矩阵
classLabels - 数据标签
C - 松弛变量
toler - 容错率
maxIter - 最大迭代次数
Returns:
oS.b - SMO算法计算的b
oS.alphas - SMO算法计算的alphas
"""
def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup=('lin', 0)):
# 初始化数据结构
oS = optStruct(np.mat(dataMatIn),np.mat(classLabels).transpose(),C,toler)
# 初始化当前迭代次数
iter = 0
entireSet = True
alphaPairsChanged = 0
# 遍历整个数据集alpha都没有更新或者超过最大迭代次数,则退出循环
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
# 遍历整个数据集
if entireSet:
for i in range(oS.m):
# 使用优化的SMO算法
alphaPairsChanged += innerL(i,oS)
print("fullSet, iter: %d i: %d, pairs changed %d" %(iter,i,alphaPairsChanged))
iter += 1
# 遍历非边界值
else:
# 遍历不在边界0和C的alpha
nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i,oS)
print("non-bound, iter: %d i:%d,pairs changed %d" %(iter,i,alphaPairsChanged))
iter += 1
# 遍历一次后改为非边界遍历
if entireSet:
entireSet = False
# 如果alpha没有更新,计算全样本遍历
elif (alphaPairsChanged == 0):
entireSet = True
print("iteration number: %d" % iter)
# 返回SMO算法计算的b和alphas
return oS.b,oS.alphas
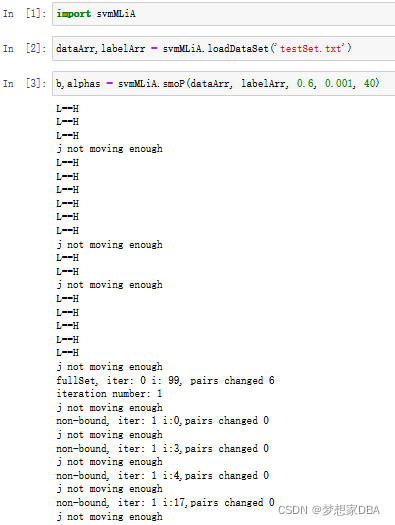
"""
函数说明:计算w
Returns:
dataArr - 数据矩阵
classLabels - 数据标签
alphas - alphas值
Returns:
w - 直线法向量
"""
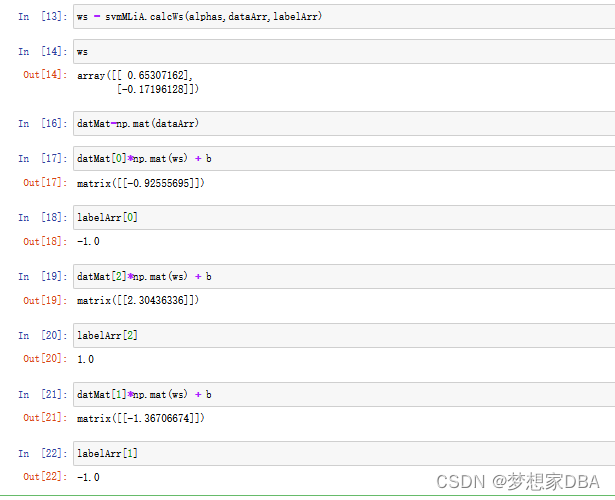
def calcWs(alphas, dataArr, classLabels):
X = np.mat(dataArr)
labelMat = np.mat(classLabels).transpose()
m, n = np.shape(X)
w = np.zeros((n,1))
for i in range(m):
w += np.multiply(alphas[i] * labelMat[i], X[i, :].T)
return w
?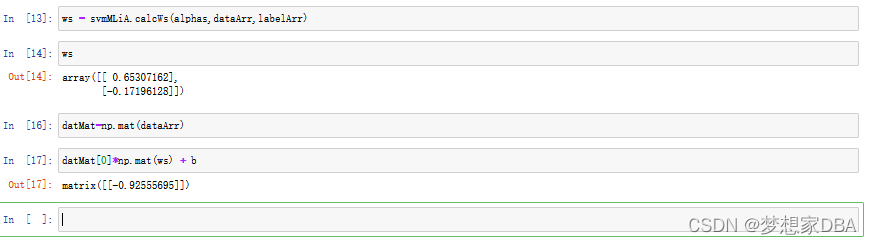
?If this value is greater than 0 ,then its class is a 1, and the class is -1 if it's less than 0.
6.5 Using kernels for more complex data
6.5.1 Mapping data to higher dimensions with kernels
Transforming the data from one feature space to another so that you can deal with it easily with your existing tools.Mathematician like to call this mapping from one feature space to another feature space.Usually, this mapping goes from a lower-dimensional feature space to a higher-dimensionaal space.
This mapping from one feature space to another is done by a kernel.
One great thing about the SVM optimization is that all operations can be written in terms of inner products. Inner products are two vectors multiplied together to yield a scalar or single number. We can replace the inner products with our kernel functions without making simplications. Replacing the inner product with a kernel is known as the kernel trick or kernel substation.
Kernel aren't unique to support vector machines.A number of other machine learning algorithms can use kernels. A popular kernel is the radial bias function.
6.5.2 The radial bias function as a kernel
The radial bias function is a kernel that's often used with support vector machines .
?
?
'''
Author: Maxwell Pan
Date: 2022-04-21 12:07:54
LastEditTime: 2022-04-25 14:36:25
FilePath: \cp06\svmMLiA.py
Description:
Software:VSCode,env:
'''
# Helper functions for the SMO algorithm
import random
import numpy as np
from time import sleep
import matplotlib.pyplot as plt
# input file data
def loadDataSet(fileName):
# data Matrix
dataMat = []
# label vector
labelMat = []
# open file
fr = open(fileName)
# read line gradually
for line in fr.readlines():
# 去掉每一行首尾的空白符,例如'\n','\r','\t',' '
# 将每一行内容根据'\t'符进行切片
lineArr = line.strip().split('\t')
# 添加数据(100个元素排成一行)
dataMat.append([float(lineArr[0]),float(lineArr[1])])
# 添加标签(100个元素排成一行)
labelMat.append(float(lineArr[2]))
return dataMat,labelMat
# m为alpha参数个数,i - alpha ,随机输出与i不通过的j
def selectJrand(i,m):
j = i
while (j==i):
# uniform() 方法将随机生成一个实数,它在[x,y]范围内
j = int(random.uniform(0,m))
return j
"""
函数说明:修剪alpha
Parameters:
aj - alpha值
H - alpha 上限
L - alpha 下限
Returns:
aj - alpha值
Modify:
2022-04-23
"""
def cliAlpha(aj, H, L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
# The simplified SMO algorithm
"""
函数说明: 简化版SMO 算法
Parameters:
dataNatIn - 数据矩阵
classLabels - 数据标签
C - 松弛变量
toler - 容错率
maxIter - 最大迭代次数
Returns:
None
Modify:
2022-04-23
"""
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
# the dataset, the class labels, a constant C , the tolerance,
# and the maximum number of iteration before quitting
dataMatrix = np.mat(dataMatIn);labelMat = np.mat(classLabels).transpose()
b = 0; m,n = np.shape(dataMatrix)
alphas = np.mat(np.zeros((m,1)))
iter = 0
while (iter < maxIter):
alphaPairsChanged = 0 # alphaPairsChanged 是否已进行优化
for i in range(m):
# 即公式为f(xi) = ∑alpha_mi*y_mi*x_mi*xi.T + b 可理解为距离 f(x)为m维行向量
fxi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
Ei = fxi - float(labelMat[i]) # 计算偏差
# 判断条件:正负间隔均判断,同时检查alpha值,保证其不等于C或者0
if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
j = selectJrand(i,m) #取不同于i的j
fxj = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
Ej = fxj -float(labelMat[j])
alphaIold = alphas[i].copy()
alphaJold = alphas[j].copy()
# 计算L、H,即alpha_j的上下界
if (labelMat[i] != labelMat[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C+alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C,C + alphas[j] + alphas[i])
if L==H:
#print("L==H");
continue
# η=-(K11+K22?2K12)也可去掉负号,但相应更新alpha_j时累减改成累加
eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
if eta >= 0:
#print("eta>=0");
continue
# 更新alpha_j
alphas[j] -= labelMat[j]*(Ei - Ej)/eta
alphas[j] = cliAlpha(alphas[j],H,L)
if (abs(alphas[j] - alphaJold) < 0.00001):
print("j not moving enough");
continue
# 更新alpha_i
alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])
# 更新阈值b
b1 = b - Ei -labelMat[i]*(alphas[i] - alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
b2 = b - Ej -labelMat[i]*(alphas[i] - alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
if (0 < alphas[i]) and (C > alphas[i]):
b = b1
elif (0 < alphas[j]) and (C > alphas[j]):
b = b2
else:
b = (b1 + b2)/2.0
alphaPairsChanged += 1
# print("iter: %d i: %d, pairs changed %d" %(iter,i,alphaPairsChanged))
if (alphaPairsChanged == 0):
iter += 1
else:
iter = 0
# print("iteration number: %d" % iter)
return b,alphas
# Support functions for full Platt SMO
# 1. 构建一个数据结构存储所有数据
class optStruct:
def __init__(self,dataMatIn, classLabels, C, toler):
self.X = dataMatIn
self.labelMat = classLabels
self.C = C
self.tol = toler
self.m = np.shape(dataMatIn)[0]
self.alphas = np.mat(np.zeros((self.m,1)))
self.b = 0
self.eCache = np.mat(np.zeros((self.m,2))) # Error cache # 误差缓存 第一列是eCache是否有效的标志位,第二列是实际E值
# 2. 计算k处误差值
def calcEk(oS, k):
# fXk = float(np.multiply(oS.alphas,oS.labelMat).T*(oS.X*oS.X[k,:].T)) + oS.b
fXk = float(np.multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
Ek = fXk - float(oS.labelMat[k])
return Ek
# 3. 用于选择第二个α
def selectJ(i, oS, Ei):
maxK = -1;maxDeltaE = 0; Ej = 0 # Inner-loop heuristic
oS.eCache[i] = [1, Ei]
validEcacheList = np.nonzero(oS.eCache[:,0].A)[0] # nonzero 返回数组中非零元素的索引值
if(len(validEcacheList)) > 1:
# 遍历一遍上列表,找出最大差值的Ej
for k in validEcacheList:
if k == i:
continue
Ek = calcEk(oS,k)
deltaE = abs(Ei - Ek)
if(deltaE > maxDeltaE):
maxK = k;
maxDeltaE = deltaE; # Choose j for maximum step size
Ej = Ek
return maxK,Ej
else:
# 第一次,直接随机寻找一个Ej
j = selectJrand(i,oS.m)
Ej = calcEk(oS, j)
return j, Ej
# 4. 计算k处误差值 并存入eCache中
def updateEk(oS, k):#after any alpha has changed update the new value in the cache
Ek = calcEk(oS, k)
oS.eCache[k] = [1,Ek]
# Full Platt SMO optimization routine
# 5. 内部循环,找到配对Ej,则返回1,
"""
函数说明:优化的SMO算法
Parameters:
i - 标号为i的数据的索引值
oS - 数据结构
Returns:
1 - 有任意一对 alpha值发生变化
0 - 没有任意一对alpha值发生变化或变化太小
"""
def innerL(i, oS):
# 步骤1: 计算误差Ei
Ei = calcEk(oS, i)
# 优化alpha,设定一定的容错率
if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
# 使用内循环启发方式2 选择alpha_j,并计算Ej
j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
# 保存更新前的alpha值,使用深层拷贝
alphaIold = oS.alphas[i].copy()
alphaJold = oS.alphas[j].copy()
# 步骤2 : 计算上下界H和下界L
if (oS.labelMat[i] != oS.labelMat[j]):
L = max(0, oS.alphas[j] - oS.alphas[i])
H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
else:
L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
H = min(oS.C, oS.alphas[j] + oS.alphas[i])
if L==H:
print("L==H");
return 0
# 步骤3:计算eta
# eta = 2.0 * oS.X[i, :] * oS.X[j, :].T - oS.X[i, :] * oS.X[i, :].T - oS.X[j, :] * oS.X[j, :].T
eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j]
if eta >= 0:
print("eta>=0")
return 0
# 步骤4:更新alpha_i
oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
# 步骤5:修剪alpha_j
oS.alphas[j] = cliAlpha(oS.alphas[j],H,L)
# 更新Ej至误差缓存
updateEk(oS, j) #added this for the Ecache
if (abs(oS.alphas[j] - alphaJold) < 0.00001):
print("j not moving enough")
return 0
# 步骤6:更新alpha_i
oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
# 更新Ei至误差缓存
updateEk(oS, i) #added this for the Ecache #the update is in the oppostie direction
# 步骤7:更新b_1 和 b_2:
# b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[i, :].T - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.X[j, :] * oS.X[i, :].T
b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i,i] - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[i,j]
# b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.X[i, :] * oS.X[j, :].T - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.X[j, :] * oS.X[j, :].T
b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i,j] - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[j,j]
#步骤8:根据b_1 和b_2更新b
if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
oS.b = b1
elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):
oS.b = b2
else:
oS.b = (b1 + b2)/2.0
return 1
else:
return 0
# Full Platt SMO outer loop
"""
函数说明: 完整的线性SMO算法
Parameters:
dataMatIn - 数据矩阵
classLabels - 数据标签
C - 松弛变量
toler - 容错率
maxIter - 最大迭代次数
Returns:
oS.b - SMO算法计算的b
oS.alphas - SMO算法计算的alphas
"""
def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup=('lin', 0)):
# 初始化数据结构
oS = optStruct(np.mat(dataMatIn),np.mat(classLabels).transpose(),C,toler)
# 初始化当前迭代次数
iter = 0
entireSet = True
alphaPairsChanged = 0
# 遍历整个数据集alpha都没有更新或者超过最大迭代次数,则退出循环
while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
alphaPairsChanged = 0
# 遍历整个数据集
if entireSet:
for i in range(oS.m):
# 使用优化的SMO算法
alphaPairsChanged += innerL(i,oS)
print("fullSet, iter: %d i: %d, pairs changed %d" %(iter,i,alphaPairsChanged))
iter += 1
# 遍历非边界值
else:
# 遍历不在边界0和C的alpha
nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
for i in nonBoundIs:
alphaPairsChanged += innerL(i,oS)
print("non-bound, iter: %d i:%d,pairs changed %d" %(iter,i,alphaPairsChanged))
iter += 1
# 遍历一次后改为非边界遍历
if entireSet:
entireSet = False
# 如果alpha没有更新,计算全样本遍历
elif (alphaPairsChanged == 0):
entireSet = True
print("iteration number: %d" % iter)
# 返回SMO算法计算的b和alphas
return oS.b,oS.alphas
"""
函数说明:计算w
Returns:
dataArr - 数据矩阵
classLabels - 数据标签
alphas - alphas值
Returns:
w - 直线法向量
"""
def calcWs(alphas, dataArr, classLabels):
X = np.mat(dataArr)
labelMat = np.mat(classLabels).transpose()
m, n = np.shape(X)
w = np.zeros((n,1))
for i in range(m):
w += np.multiply(alphas[i] * labelMat[i], X[i, :].T)
return w
# Kernel transformation function
def kernelTrans(X, A, kTup):
m,n = np.shape(X)
K = np.mat(np.zeros((m,1)))
if kTup[0] == 'lin':
K = X * A.T
elif kTup[0] == 'rbf':
for j in range(m):
deltaRow = X[j,:] - A
K[j] = deltaRow*deltaRow.T
K = np.exp(K / (-1*kTup[1]**2)) # Element-wise division
else:
raise NameError('Houston we have a Problem -- That kernel is not recognized')
return K
"""
K1越大会过拟合
类说明: 维护所有需要操作的值
Parameters:
dataMatIn - 数据矩阵
classLabels - 数据标签
C - 松弛变量
toler - 容错率
kTup - 包含核函数信息的元组,第一个参数存放该核函数类别,第二个参数存放必要的核函数需要用到的参数。
Returns:
None
"""
class optStruct:
def __init__(self, dataMatIn, classLabels, C, toler, kTup):
# 数据矩阵
self.X = dataMatIn
# 数据标签
self.labelMat = classLabels
# 松弛变量
self.C = C
# 容错率
self.tol = toler
# 矩阵的行数
self.m = np.shape(dataMatIn)[0]
# 根据矩阵行数初始化alphas矩阵,一个m行1列的全零列向量
self.alphas = np.mat(np.zeros((self.m,1)))
# 初始化b 参数为0
self.b = 0
# 根据矩阵行数初始化误差缓存矩阵,第一列为是否有效标志位,第二列为实际的误差E的值
self.eCahe = np.mat(np.zeros((self.m,2)))
# 初始化核K
self.K = np.mat(np.zeros((self.m,self.m)))
# 计算所有数据的核K
for i in range(self.m):
self.K[:, i] = kernelTrans(self.X, self.X[i,:], kTup)

?6.5.3 Using a kernel for testing
"""
函数说明:测试函数
Parameters:
k1 - 使用高斯核函数的时候表示到达率
Returns:
None
"""
def testRbf(k1 = 1.3):
# 加载训练集
dataArr,labelArr = loadDataSet('testSetRBF.txt')
# 根据训练集计算b,alphas
b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 100, ('rbf', k1))
datMat = np.mat(dataArr)
labelMat = np.mat(labelArr).transpose()
# 获得支持向量
svInd = np.nonzero(alphas.A > 0)[0]
sVs = datMat[svInd]
labelSV = labelMat[svInd]
print("支持向量个数:%d" % np.shape(sVs)[0])
m,n = np.shape(datMat)
errorCount = 0
for i in range(m):
# 计算各个点的核
kernelEval = kernelTrans(sVs, datMat[i, :], ('rbf', k1))
# 根据支持向量的点计算超平面,返回预测结果
predict = kernelEval.T * np.multiply(labelSV,alphas[svInd]) + b
# 返回数组中各元素的正负号,用1 和 -1 表示,并统计错误个数
if np.sign(predict)!= np.sign(labelArr[i]):
errorCount += 1
# 打印错误率
print("训练集错误率:%.2f%%" % ((float(errorCount) / m) * 100))
# 加载测试集
dataArr,labelArr = loadDataSet('testSetRBF2.txt')
errorCount = 0
datMat = np.mat(dataArr)
labelMat = np.mat(labelArr).transpose()
m,n = np.shape(datMat)
for i in range(m):
# 计算各个点的核
kernelEval = kernelTrans(sVs, datMat[i, :],('rbf', k1))
# 根据支持向量的点计算超平面,返回预测结果
predict = kernelEval.T * np.multiply(labelSV, alphas[svInd]) + b
# 返回数组中各元素的正负号,用1 和-1 表示,并统计错误个数
if np.sign(predict) != np.sign(labelArr[i]):
errorCount += 1
# 打印错误率
print("训练集错误率:%.2f%%" % ((float(errorCount) / m) * 100))"""
K1越大会过拟合
类说明: 维护所有需要操作的值
Parameters:
dataMatIn - 数据矩阵
classLabels - 数据标签
C - 松弛变量
toler - 容错率
kTup - 包含核函数信息的元组,第一个参数存放该核函数类别,第二个参数存放必要的核函数需要用到的参数。
Returns:
None
"""
class optStruct:
def __init__(self, dataMatIn, classLabels, C, toler, kTup):
# 数据矩阵
self.X = dataMatIn
# 数据标签
self.labelMat = classLabels
# 松弛变量
self.C = C
# 容错率
self.tol = toler
# 矩阵的行数
self.m = np.shape(dataMatIn)[0]
# 根据矩阵行数初始化alphas矩阵,一个m行1列的全零列向量
self.alphas = np.mat(np.zeros((self.m,1)))
# 初始化b 参数为0
self.b = 0
# 根据矩阵行数初始化误差缓存矩阵,第一列为是否有效标志位,第二列为实际的误差E的值
self.eCahe = np.mat(np.zeros((self.m,2)))
# 初始化核K
self.K = np.mat(np.zeros((self.m,self.m)))
# 计算所有数据的核K
for i in range(self.m):
self.K[:, i] = kernelTrans(self.X, self.X[i,:], kTup)
"""
函数说明:测试函数
Parameters:
k1 - 使用高斯核函数的时候表示到达率
Returns:
None
"""
def testRbf(k1 = 1.3):
# 加载训练集
dataArr,labelArr = loadDataSet('testSetRBF.txt')
# 根据训练集计算b,alphas
b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1))
datMat = np.mat(dataArr)
labelMat = np.mat(labelArr).transpose()
# 获得支持向量
svInd = np.nonzero(alphas.A > 0)[0]
sVs = datMat[svInd]
labelSV = labelMat[svInd]
print("支持向量个数:%d" % np.shape(sVs)[0])
m,n = np.shape(datMat)
errorCount = 0
for i in range(m):
# 计算各个点的核
kernelEval = kernelTrans(sVs, datMat[i, :], ('rbf', k1))
# 根据支持向量的点计算超平面,返回预测结果
predict = kernelEval.T * np.multiply(labelSV,alphas[svInd]) + b
# 返回数组中各元素的正负号,用1 和 -1 表示,并统计错误个数
if np.sign(predict)!= np.sign(labelArr[i]):
errorCount += 1
# 打印错误率
print("训练集错误率:%.2f%%" % ((float(errorCount) / m) * 100))
# 加载测试集
dataArr,labelArr = loadDataSet('testSetRBF2.txt')
errorCount = 0
datMat = np.mat(dataArr)
labelMat = np.mat(labelArr).transpose()
m,n = np.shape(datMat)
for i in range(m):
# 计算各个点的核
kernelEval = kernelTrans(sVs, datMat[i, :],('rbf', k1))
# 根据支持向量的点计算超平面,返回预测结果
predict = kernelEval.T * np.multiply(labelSV, alphas[svInd]) + b
# 返回数组中各元素的正负号,用1 和-1 表示,并统计错误个数
if np.sign(predict) != np.sign(labelArr[i]):
errorCount += 1
# 打印错误率
print("训练集错误率:%.2f%%" % ((float(errorCount) / m) * 100))