开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 高级数据结构(二)—线段树及其应用 -> 正文阅读

[数据结构与算法]高级数据结构(二)—线段树及其应用

- 本人的LeetCode账号：魔术师的徒弟，欢迎关注获取每日一题题解，快来一起刷题呀~

本人Gitee账号：路由器，欢迎关注获取博客内容源码。
文章目录

一、单点修改的线段树

1 线段树的原理及其基本操作

一个最简单的线段树一般会提供五个操作：

pushup(u)：根据子结点信息来算父节点的信息；

build():将一段区间初始化为线段树；

modify():修改操作，修改单点(easy)或修改某个区间(使用pushdown，比较hard的一个操作)

query()：查询操作，查询某一端区间的信息。

pushdown()：把当前父节点的修改信息下传到子结点。

??线段树是一个满二叉树，假设要用线段树维护1~10的闭区间。

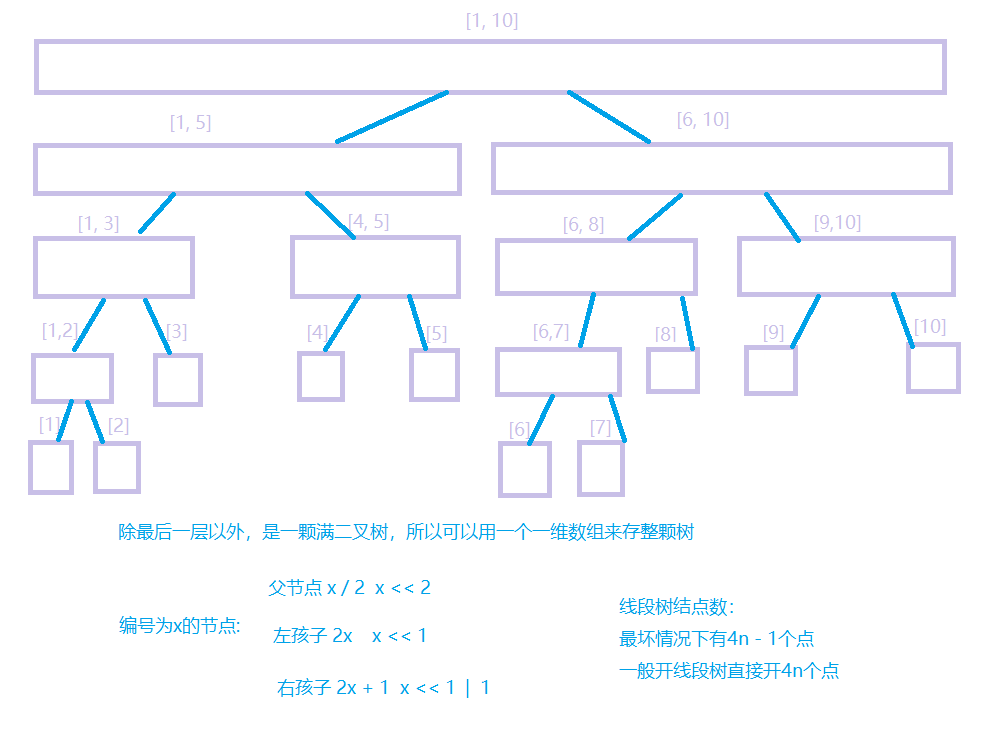
??先看看build操作的伪代码：

??要注意的是，是建完结点回来然后根据子结点信息更新父节点信息。

??再看看query操作的伪代码，比如我们要查询某区间的最大值，每个结点存当前区间的最大值。

??假设查[5, 9]的最大值：

??证明查询时总访问的区间数量一定是在log(n)范围内。

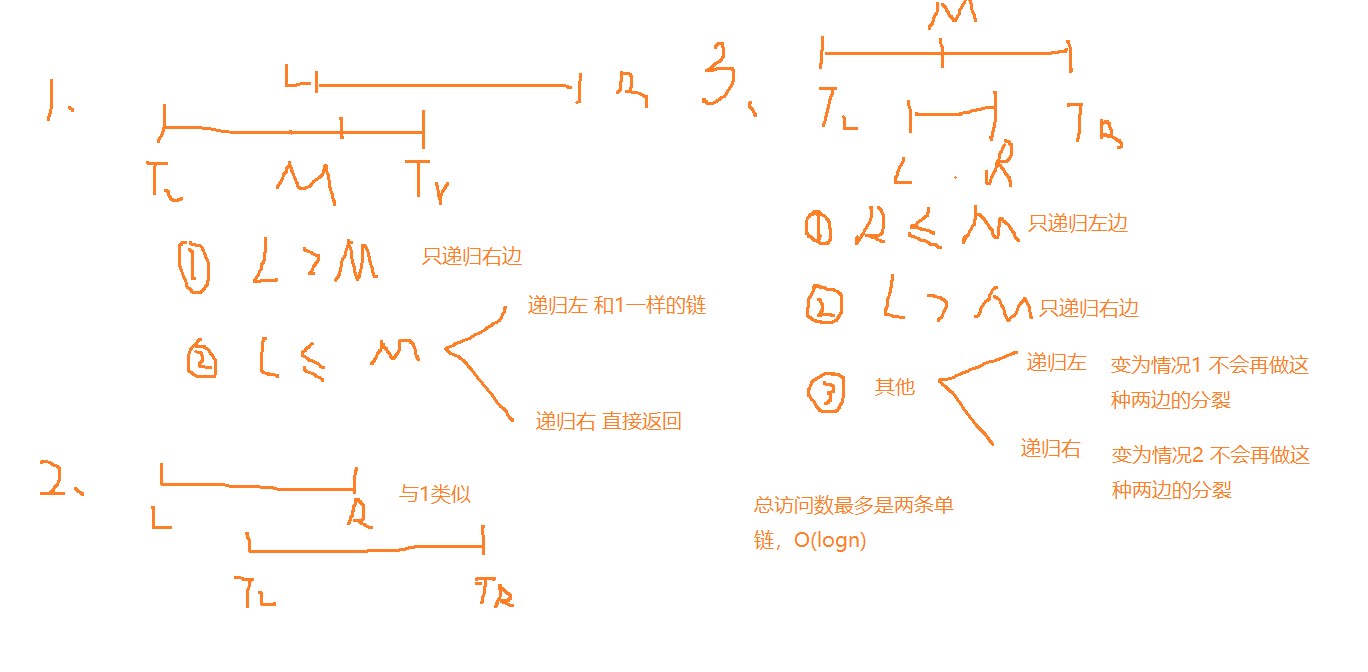
??每个1 2情况展开有两个点，估算一下最多有4logn个点，这一点，比树状数组的复杂度常数上要高一些。

??modify单点修改：直接递归就好了，比如要更新6这个点：

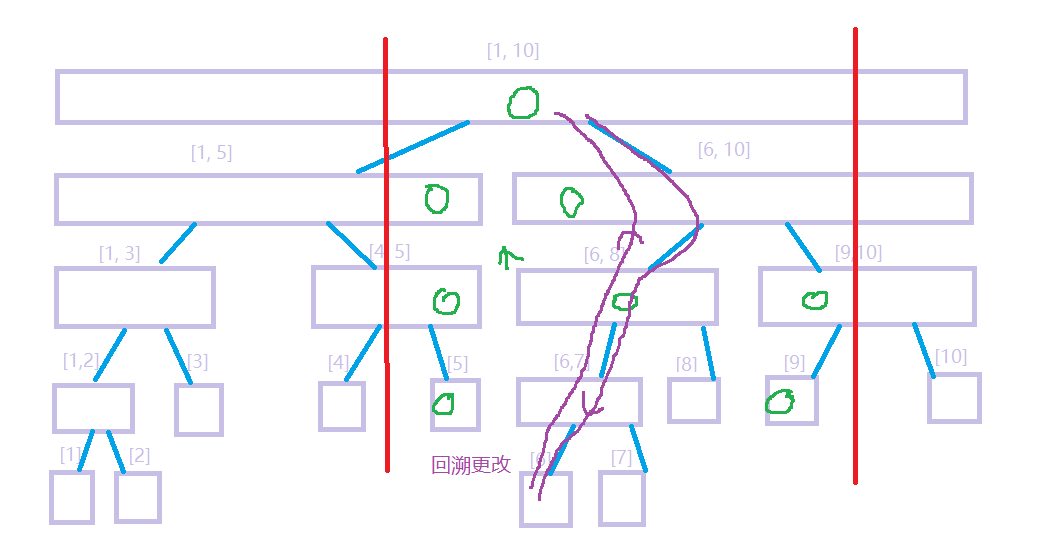
2 Acwing1275 最大数

??如果要动态的添加点是在是太难了，因为最多有m个数，所以我们可以直接开m个坑，用n维护当前有多少个位置已经被占了，增加操作相当于把n + 1位置的数修改为我们要添加的数，然后n++。

??所以我们总共需要两个操作：

在某一个位置修改一个数；
询问[n - L + 1, n]区间内的最大值；

??这就是线段树的一个经典操作。

??线段树首先需要一个结点，首先必然要存的是左端点和右端点l和r，然后在本题中，我们另外需要存储的就是区间内的最大值。

??如何判断线段树中要存什么信息？看看问的是某个区间的某种属性，一般问的属性要存下来，有时候可能还要存辅助信息，一般就看看当前属性能否由两个子树的属性求出来，如果不能就增加一下属性，能的话就ok了。

#include <iostream>
#include <cstdio>
using namespace std;
typedef long long LL;

const int N = 200010;
int m, p;


struct Node
{
    int l, r;
    int v;// 区间[l, r]中的最小值
}tr[4 * N];

// 建线段树
void build(int u, int l, int r)
{
    tr[u] = { l, r };
    // 如果左右端点相同 则返回
    if (l == r) return;
    // 递归建立左端点和右端点
    int mid = (l + r) >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
    // 本题不需要pushup(u) 因为max一开始大家都是0 就不用了
}

// 根据子结点的信息来更新父节点u的信息
void pushup(int u)
{
    tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);
}

// 查询区间[l, r]的最大值
int query(int u, int l, int r)
{
    // 如果[l, r] 完全包含[Tl, Tr] 则直接返回
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;
    
    // 取中间点
    int mid = tr[u].l + tr[u].r >> 1;
    int v = 0;
    // 看看和左边有没有交集
    if (l <= mid) v = query(u << 1, l, r);
    // 看看和右边有没有交集
    if (r > mid) v = max(v, query(u << 1 | 1, l, r));
    return v;
}

// 单点修改
void modify(int u, int x, int v)
{
    // 如果就是当前点 修改后直接返回
    if (tr[u].l == x && tr[u].r == x)
    {
        tr[u].v = v;
        return;
    }
    // 否则看看在左边还是右边 决定递归左边还是右边
    int mid = tr[u].l + tr[u].r >> 1;
    // 如果在左区间 就递归左区间
    if (mid >= x) modify(u << 1, x, v);
    else modify(u << 1 | 1, x, v);
    // 用子结点更新父节点信息
    pushup(u);
}


int main()
{
    cin >> m >> p;
    int n = 0;
    // 建树 直接建m个点的树
    build(1, 1, m);
    int t;
    int last;
    char op[2];
    while (m--)
    {
        scanf("%s%d", op, &t);
        // 查询操作
        if (op[0] == 'Q')
        {
            last = query(1, n - t + 1, n);
            printf("%d\n", last);
        }
        // 增加操作
        else 
        {
            modify(1, n + 1, ((LL)t + last) % p);
            ++n;
        }
    }
    return 0;
}

??单点修改，动态维护区间的最大值：

#include <iostream>
#include <cstdio>
using namespace std;
typedef long long LL;

const int N = 200010;


struct Node
{
    int l, r;
    int v;// 区间[l, r]中的最小值
}tr[4 * N];

// 建线段树
void build(int u, int l, int r)
{
    tr[u] = { l, r };
    // 如果左右端点相同 则返回
    if (l == r) return;
    // 递归建立左端点和右端点
    int mid = (l + r) >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
    // 本题不需要pushup(u) 因为max一开始大家都是0 就不用了
}

// 根据子结点的信息来更新父节点u的信息
void pushup(int u)
{
    tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);
}

// 查询区间[l, r]的最大值
int query(int u, int l, int r)
{
    // 如果[l, r] 完全包含[Tl, Tr] 则直接返回
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;
    
    // 取中间点
    int mid = tr[u].l + tr[u].r >> 1;
    int v = 0;
    // 看看和左边有没有交集
    if (l <= mid) v = query(u << 1, l, r);
    // 看看和右边有没有交集
    if (r > mid) v = max(v, query(u << 1 | 1, l, r));
    return v;
}

// 单点修改
void modify(int u, int x, int v)
{
    // 如果就是当前点 修改后直接返回
    if (tr[u].l == x && tr[u].r == x)
    {
        tr[u].v = v;
        return;
    }
    // 否则看看在左边还是右边 决定递归左边还是右边
    int mid = tr[u].l + tr[u].r >> 1;
    // 如果在左区间 就递归左区间
    if (mid >= x) modify(u << 1, x, v);
    else modify(u << 1 | 1, x, v);
    // 用子结点更新父节点信息
    pushup(u);
}

3 Acwing245.你能回答这些问题吗

??更新策略如下：

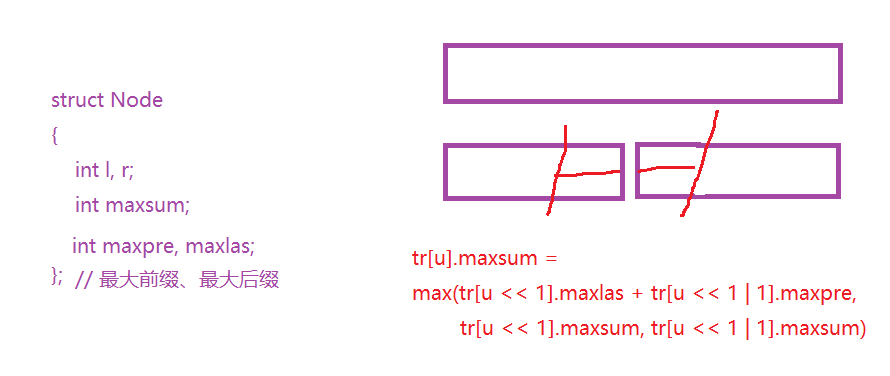
#include <cstdio>
#include <iostream>
using namespace std;

const int N = 500010;

struct Node
{
    int l, r;
    int tmax, lmax, rmax, sum;
}tr[N * 4];

int w[N];
int n, m;

void merge(Node& u, Node& l, Node& r)
{
    u.sum = l.sum + r.sum;
    u.lmax = max(l.lmax, l.sum + r.lmax);
    u.rmax = max(r.rmax, r.sum + l.rmax);
    u.tmax = max(max(l.tmax, r.tmax), l.rmax + r.lmax);
}

void pushup(int u)
{
    merge(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void build(int u, int l, int r)
{
    if (l == r)
    {
        tr[u] = { r, r, w[r], w[r], w[r], w[r] };
        return;
    }
    else 
    {
        tr[u] = { l, r };
        int mid = (l + r) >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

void modify(int u, int x, int v)
{
    if (tr[u].l == x && tr[u].r == x)
    {
        tr[u] = { x, x, v, v, v, v };
        return;
    }
    int mid = tr[u].l + tr[u].r >> 1;
    if (x <= mid) modify(u << 1, x, v);
    else modify(u << 1 | 1, x, v);
    pushup(u);
}

Node query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r)
    {
        return tr[u];
    }
    int mid = tr[u].l + tr[u].r >> 1;
    // 只在左半边
    if (r <= mid) return query(u << 1, l, r);
    // 只在右半边
    else if (l > mid) return query(u << 1 | 1, l, r);
    else
    {
        // 两边都有
        auto left = query(u << 1, l, r);
        auto right = query(u << 1 | 1, l, r);
        Node res;
        // 合并
        merge(res, left, right);
        return res;
    }
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);
    build(1, 1, n);
    int k, x, y;
    while (m--)
    {
        scanf("%d%d%d", &k, &x, &y);
        if (k == 1)
        {
            if (x > y) swap(x, y);
            int res = query(1, x, y).tmax;
            printf("%d\n", res);
        }
        else 
        {
            modify(1, x, y);
        }
    }
    return 0;
}

4 Acwing246.区间的最大公约数

??考虑线段树结点需要存的信息，首先要存最大公约数，然后考虑怎么由左区间的最大公约数和右区间的最大公约数得到父节点的最大公约数：
$g c d ([L, R]) = g c d (g c d ([L, m i d]), g c d ([m i d + 1, R]))$
??即父区间的最大公约数等于左区间的最大公约数与右区间的最大公约数再取一个最大公约数，那么查询操作就只存最大公约数就够了。

??发现对于一个区间同时增加1个数非常难以操作，如果每次只修改一个数，那么非常好操作（一个数的最大公约数就是它自己）。

??所以有没有什么方法可以把区间的修改变成单点的修改？

??联想到了差分的技巧。

??注意到有等式：
$a_1, a_2, ..., a_n) = (a_1, a_2 - a_1, a_3 - a_2,...,a_n - a_{n - 1})$
Proof：
$假设d =(a_1, a_2, ..., a_n),证明它一定是右边这n个数的一个约数\\ 这是显然的，右边的每一项都整除d，又因为右边是右边n个数的最大公约数\\ 所以d<=(a_1, a_2 - a_1, a_3 - a_2,...,a_n - a_{n - 1})\\ 设d =(a_1, a_2 - a_1, a_3 - a_2,...,a_n - a_{n - 1})\\ 首先d能整除a_1,有因为d能整除a_1且能整除a_2 - a_1\\ 所以d能整除他们的和,a_2\\ 以此类推，d能整除a_1到a_n中的每一个数\\ 所以d是a_1-a_n的公约数\\ 所以d<=(a_1, a_2, ..., a_n)\\ 综上，(a_1, a_2, ..., a_n) = (a_1, a_2 - a_1, a_3 - a_2,...,a_n - a_{n - 1})$
??所以一个数列的最大公约数等于其差分数列的最大公约数，如果要对原数列进行区间整体加x，那么对差分数列进行两个单点增加即可。

??所以如果要求区间[L,R]的最大公约数，只要求a[L], b[L + 1], ..., b[R]的最大公约数即可，右边很好维护，也很好求。

??a[L]就是要求一个前缀和，所以我们需要求的是：
$g c d (a [L], g c d (b [L + 1], . . ., b [R]))$
??所以维护两个信息：sum和gcd，差分序列的前缀和和差分序列的最大公约数，因为他们维护的是统一个序列，所以可以放在一起写。

#include <iostream>
#include <cstdio>
using namespace std;

// 本题数据范围需要用long long
typedef long long LL;

// 一个gcd
LL gcd(LL a, LL b)
{
    return b ? gcd(b, a % b) : a;
}

const int N = 500010;

LL w[N];// 原数组

struct Node
{
    int l, r;
    // 线段树中维护差分数组
    // 因为查询操作最后需要的是(1, L)的前缀和和[L + 1, R]的最大公约数
    // 所以维护一个区间的和和一个最大公约数
    LL d, sum;
}tr[N * 4];

void merge(Node& u, Node& l, Node& r)
{
    u.sum = l.sum + r.sum;
    u.d = gcd(l.d, r.d);
}

void pushup(int u)
{
    merge(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void build(int u, int l, int r)
{
    if (l == r)
    {
        // 差分数组
        tr[u] = { r, r, w[r] - w[r - 1], w[r] - w[r - 1] };
        return;
    }
    tr[u] = {l, r};
    int mid = l + r >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
    pushup(u);
}

void modify(int u, int x, LL v)
{
    if (tr[u].l == x && tr[u].r == x)
    {
        // 注意 我们这里的单点修改是增加
        tr[u].sum += v;
        tr[u].d += v;
        return;
    }
    int mid = tr[u].l + tr[u].r >> 1;
    if (x <= mid) modify(u << 1, x, v);
    else modify(u << 1 | 1, x, v);
    pushup(u);
}

Node query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r)
    {
        return tr[u];
    }
    int mid = tr[u].l + tr[u].r >> 1;
    if (r <= mid) return query(u << 1, l, r);
    if (l > mid) return query(u << 1 | 1, l, r);
    auto left = query(u << 1, l, r);
    auto right = query(u << 1 | 1, l, r);
    Node res;
    merge(res, left, right);
    return res;
}


int n, m;

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) scanf("%lld", &w[i]);
    // 建立线段树
    build(1, 1, n);
    int l, r;
    LL d;
    char op[2];
    // 读入操作
    while (m--)
    {
        scanf("%s", op);
        // 查询操作
        if (op[0] == 'Q')
        {
            scanf("%d%d", &l, &r);
            // a[l] 对应差分数组的前缀和
            auto left = query(1, 1, l);
            // [L + 1, R]的最大公约数
            Node right({0, 0, 0, 0});
            if (l + 1 <= r) right = query(1, l + 1, r);
            // 正的约数
            LL res = abs(gcd(left.sum, right.d));
            printf("%lld\n", res);
        }
        // 修改操作
        else
        {
            scanf("%d%d%lld", &l, &r, &d);
            // 利用差分 把转化为差分数组的l这一点 + 1 r + 1这一点-1
            modify(1, l, d);
            if (r + 1 <= n) modify(1, r + 1, -d);
        }
    }
    return 0;
}

二、区间修改的线段树

1 原理

懒标记：pushdown，把父节点信息下传子结点；
扫描线法

??什么是懒标记？如果只有pushup操作，那么我们只能做单点修改，如果用单点修改来修改区间，最坏情况下要修改O(n)个区间，为了解决这个问题，提出了pushdown操作。

??它的思想与query类似，当我们查询到一个区间被完全包含的时候，就不往下走了，直接打上一个懒标记。

??以区间和为例：

??区间属性中增加一个add懒标记，其含义为给以当前结点为根的子树中的每一个结点都修改（加上）这个数（不包含当前区间自己），这样可以保证我们的修改的操作时间复杂度在O(LOGN)内。

??查询时：我们用到的每一个区间的值，必须要把祖宗的懒标记加上，因此我们增加一个操作，如果当前区间不符合要求，我们就先把它的懒标记清空，然后传给两个孩子结点，这样的操作就是pushdown操作，加上了这种操作时，计算某区间和时，递归到单点时，其祖宗的懒标记就已经全部清空（被计算过了）了，累加到了根节点上。

// 懒标记传递到子区间
root add;
left.add += root.add; left.sum += (left.r - left.l + 1) * root.add;
right.add += root.add; right.sum += (right.r - left.l + 1) * root.add;
root.add = 0;

??对于修改操作，如果我们仅仅要修改当前区间的某一部分，那么一定要把懒标记往子孙传，否则可能会出现一个区间的左右两部分懒标记不同。

2 Acwing243.简单的整数问题

??线段树结点中维护两个信息：

sum:如果考虑当前结点及子结点上的所有标记，当前区间和为多少（没有考虑祖先结点的标记）。
add:给当前区间的所有儿子（不包括它自己）加上add。

#include <iostream>
using namespace std;

const int N = 1e5 + 10;
// 1e5个1e9 可能爆int
typedef long long LL;

struct Node
{
    int l, r;
    // sum:进考虑当前结点以及子节点的懒标记时 当前区间和
    // add:当前区间的全部子结点都要加的数
    LL sum, add;
}tr[N * 4];

int w[N];

// pushup 根据子结点更新父节点
void pushup(int u)
{
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

// pushdown 把懒标记下传
void pushdown(int u)
{
    auto& root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1];
    // 如果当前区间懒标记不为0 则下传
    if (root.add != 0)
    {
        // 更新子区间懒标记增加root.add
        left.add += root.add;
        // 区间和增加为区间元素个数*add
        left.sum += (LL)root.add * (left.r - left.l + 1);
        right.add += root.add;
        right.sum += (LL)root.add * (right.r - right.l + 1);
        // 根节点的懒标记置0
        root.add = 0;
    }
}

// build操作 和没有懒标记的一样
void build(int u, int l, int r)
{
    if (l == r)
    {
        tr[u] = {r, r, w[r], 0};
        return;
    }
    tr[u] = {l, r};
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    pushup(u);
}

// modify 区间修改 [l, r]增加d
void modify(int u, int l, int r, int d)
{
    // 如果当前所在结点被包在[l, r]内
    if (tr[u].l >= l && tr[u].r <= r)
    {
        tr[u].sum += (LL)d * (tr[u].r - tr[u].l + 1);// 当前区间增加d * 区间长度
        tr[u].add += d;// 当前区间懒标记增加d
        return;
    }
    // 否则 说明当前结点区间和[l,r]仅是有重合部分
    // 会有部分修改
    // 所以先把懒标记传下去
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    // 看看是否与左区间相交
    if (l <= mid) modify(u << 1, l, r, d);
    // 看看是否与右区间相交
    if (r > mid) modify(u << 1 | 1, l, r, d);
    // 修改后要根据子结点信息更新父节点信息
    pushup(u);
}

// query:区间查询[l, r]
LL query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r)
    {
        return tr[u].sum;
    }
    // 否则查询的区间并没有完全包住当前区间 
    // 为了保证子区间值正确
    // 需要pushdown
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    if (r <= mid) return query(u << 1, l, r);
    if (l > mid) return query(u << 1 | 1, l, r);
    return query(u << 1, l, r) + query(u << 1 | 1, l, r);
}

int n, m;

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);
    build(1, 1, n);
    int l, r, d;
    char op[2];
    while (m--)
    {
        scanf("%s%d%d", op, &l, &r);
        if (op[0] == 'C')
        {
            scanf("%d", &d);
            modify(1, l, r, d);
        }
        else 
        {
            printf("%lld\n", query(1, l, r));
        }
    }
    return 0;
}

3 区间加d 求区间和的线段树模板

??简单写了个模板：

struct Node
{
    int l, r;
    LL sum, add;
};

class SegmentTree
{
    typedef long long LL;
public:
    template<class InputIterator> 
    SegmentTree(InputIterator first, InputIterator last)
    {
        int i = 1;
        while (first != last)
        {
            w[i] = *first;
            ++first;
            ++i;
        }
        n = i - 1;
        build(1, 1, n);
    }
    
    void pushup(int u)
    {
        tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
    }
    
    // 下传懒标记 在区间需要分裂时用
    void pushdown(int u)
    {
        auto& root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1];
        if (root.add)
        {
            left.add += root.add;
            left.sum += (LL)root.add * (left.r - left.l + 1);
            right.add += root.add;
            right.sum += (LL)root.add * (right.r - right.l + 1);
            root.add = 0;
        }
    }
    
    // 建树
    void build(int u, int l, int r)
    {
        if (l == r)
        {
            tr[u] = {r, r, w[r], 0};
            return;
        }
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
    
    // modify [l, r] += d
    void modify(int l, int r, int d)
    {
        _modify(1, l, r, d);
    }
    
    // _modify递归子函数
    void _modify(int u, int l, int r, int d)
    {
        if (tr[u].l >= l && tr[u].r <= r)
        {
            // 更新懒标记
            tr[u].add += d;
            // 不必分裂 更新一下sum即可
            tr[u].sum += (LL)d * (tr[u].r - tr[u].l + 1);
            return;
        }
        // 否则就是要分裂 先下传懒标记
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) _modify(u << 1, l, r, d);
        if (r > mid) _modify(u << 1 | 1, l, r, d);
        pushup(u);
    }
    // query [l, r]的和
    LL query(int l, int r)
    {
        return _query(1, l, r);
    }
    // 递归子函数
    LL _query(int u, int l, int r)
    {
        if (tr[u].l >= l && tr[u].r <= r)
        {
            return tr[u].sum;
        }
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if (r <= mid) return _query(u << 1, l, r);
        if (l > mid) return _query(u << 1 | 1, l, r);
        return _query(u << 1, l, r) + _query(u << 1 | 1, l, r);
    }
private:
    static const int N = 1e5 + 10;
    Node tr[N * 4];
    int w[N];
    int n;
};

4 Acwing1277. 维护序列

??思路：

#include <iostream>
using namespace std;

const int N = 1e5 + 10;

typedef long long LL;

int n, m, p;

struct Node
{
    int l, r;
    int sum;// 区间和
    int mul;// 乘法懒标记 
    int add;// 加法懒标记
    // 表示其所有子结点区间的每个数x都要 x * mul + add
}tr[N * 4];

int w[N];

void pushup(int u)
{
    tr[u].sum = (tr[u << 1].sum + tr[u << 1 | 1].sum) % p;
}

// pushdown中更新子结点懒标记的函数
// 即子结点区间中的每个数(x * t.mul + t.add) * mul + add
// x * (t.mul * mul) + (t.add * mul + add)
void eval(Node& t, int mul, int add)
{
    // 区间和 = t.sum * mul + add * (t.r - t.l + 1) 注意取模
    t.sum = ((LL)t.sum * mul + (LL)add * (t.r - t.l + 1)) % p;
    // 乘法懒标记更新 * mul
    t.mul = (LL)t.mul * mul % p;
    // 加法懒标记 t.add * mul + add
    t.add = ((LL)t.add * mul + add) % p;
}

void pushdown(int u)
{
    // 把懒标记传给左结点
    eval(tr[u << 1], tr[u].mul, tr[u].add);
    // 把懒标记传给右节点
    eval(tr[u << 1 | 1], tr[u].mul, tr[u].add);
    // 懒标记置空
    tr[u].mul = 1, tr[u].add = 0;
}

void build(int u, int l, int r)
{
    if (l == r)
    {
        // 初始时 乘法懒标记为1 加法懒标记为0
        tr[u] = {r, r, w[r], 1, 0};
        return;
    }
    tr[u] = {l, r, 0, 1, 0};
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    pushup(u);
}
// [l, r]区间的每个数x x * mul + add
void modify(int u, int l, int r, int mul, int add)
{
    if (tr[u].l >= l && tr[u].r <= r)
    {
        // 更新这个点的懒标记 
        eval(tr[u], mul, add);
        return;
    }
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    // 如果左区间有交集
    if (l <= mid) modify(u << 1, l, r, mul, add);
    // 如果右区间有交集
    if (r > mid) modify(u << 1 | 1, l, r, mul, add);
    pushup(u);
}

// [l, r]的区间和
int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r)
    {
        return tr[u].sum;
    }
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    if (r <= mid) return query(u << 1, l, r);
    if (l > mid) return query(u << 1 | 1, l, r);
    return (query(u << 1, l, r) + query(u << 1 | 1, l, r)) % p; 
}

int main()
{
    cin >> n >> p;
    for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);
    build(1, 1, n);
    scanf("%d", &m);
    int op, l, r, d;
    while (m--)
    {
        scanf("%d%d%d", &op, &l, &r);
        // [l, r] * d  x * d + 0
        if (op == 1)
        {
            scanf("%d", &d);
            modify(1, l, r, d, 0);
        }
        // [l, r] + d x * 1 + d
        else if (op == 2)
        {
            scanf("%d", &d);
            modify(1, l, r, 1, d);
        }
        else printf("%d\n", query(1, l, r));
    }
    return 0;
}

5 LCP 52.二叉树染色的线段树做法

??本题可以把染成蓝色看做是对应区间[l, r]乘以0，染成红色是对应区间[l, r]加上1，因为二叉树结点值比较大，但二叉树结点的个数是1e5数量级的，所以可以用离散化。最后，询问每个区间(i, i)的值，若不为零，说明此点为蓝色，答案加1。

struct Node 
{
    int l, r;
    int sum, mul, add;
};

class SegmentTree
{
public:
    template<class InputIterator>
    SegmentTree(InputIterator first, InputIterator last)
    {
        int i = 1;
        while (first != last)
        {
            w[i] = *first;
            first++;
            i++;
        }
        n = i - 1;
        build(1, 1, n);
    }
    SegmentTree(int sz)
    : n(sz)
    {
        memset(w, 0, sizeof(w));
        build(1, 1, n);
    }
    void modify(int l, int r, int mul, int add)
    {
        _modify(1, l, r, mul, add);
    }

    int query(int l, int r)
    {
        return _query(1, l, r);
    }
private:
    void pushup(int u)
    {
        tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
    }
    
    void eval(Node& t, int mul, int add)
    {
        t.sum = t.sum * mul + add * (t.r - t.l + 1);
        t.mul *= mul;
        t.add = t.add * mul + add;
    }

    void pushdown(int u)
    {
        eval(tr[u << 1], tr[u].mul, tr[u].add);
        eval(tr[u << 1 | 1], tr[u].mul, tr[u].add);
        tr[u].mul = 1, tr[u].add = 0;
    }

    void build(int u, int l, int r)
    {
        if (l == r)
        {
            tr[u] = {r, r, w[r], 1, 0};
            return;
        }
        tr[u] = {l, r, 0, 1, 0};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }

    void _modify(int u, int l, int r, int mul, int add)
    {
        if (tr[u].l >= l && tr[u].r <= r)
        {
            eval(tr[u], mul, add);
            return;
        }
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) _modify(u << 1, l, r, mul, add);
        if (r > mid) _modify(u << 1 | 1, l, r, mul, add);
        pushup(u);
    }

    int _query(int u, int l, int r)
    {
        if (tr[u].l >= l && tr[u].r <= r)
        {
            return tr[u].sum;
        }
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if (r <= mid) return _query(u << 1, l, r);
        if (l > mid) return _query(u << 1 | 1, l, r);
        return _query(u << 1, l, r) + _query(u << 1 | 1, l, r);
    }

    static const int N = 1e5 + 10;
    int w[N];
    Node tr[N * 4];
    int n;
};

class Solution {
public:
    vector<int> inorder;
    int getNumber(TreeNode* root, vector<vector<int>>& ops) 
    {
        Inorder(root);
        // 离散化
        unordered_map<int, int> myhash;
        int n = inorder.size();
        for (int i = 0; i < n; ++i) myhash[inorder[i]] = i + 1;
        SegmentTree SegT(n);
        for (auto& op : ops)
        {
            if (op[0] == 0)
            {
                // 染蓝 [l, r] * 0 + 0
                int l = myhash[op[1]], r = myhash[op[2]];
                SegT.modify(l, r, 0, 0);
            }
            else 
            {
                // 染红 [l, r] * 1 + 1
                int l = myhash[op[1]], r = myhash[op[2]];
                SegT.modify(l, r, 1, 1);
            }
        }
        int ans = 0;
        // 统计不为0的点
        for (int i = 1; i <= n; ++i)
        {
            if (SegT.query(i, i) != 0) ++ans;
        }
        return ans;
    }
    void Inorder(TreeNode* root)
    {
        if (root == nullptr) return;
        Inorder(root->left);
        inorder.push_back(root->val);
        Inorder(root->right);
    }
};

6 区间乘c加d 求区间和的线段树模板

??简单总结一个模板：

struct Node 
{
    int l, r;
    int sum, mul, add;
    // sum区间和
    // mul 乘法的懒标记
    // add 除法的懒标记
    // 表示它的所有子区间的每个元素x 需要进行 x * mul + add
};

class SegmentTree
{
public:
    // 迭代器区间构造
    template<class InputIterator>
    SegmentTree(InputIterator first, InputIterator last)
    {
        int i = 1;
        while (first != last)
        {
            w[i] = *first;
            first++;
            i++;
        }
        n = i - 1;
        build(1, 1, n);
    }
    // 全0构造
    SegmentTree(int sz)
    : n(sz)
    {
        memset(w, 0, sizeof(w));
        build(1, 1, n);
    }
    // x in [l, r] x = x * mul + add
    void modify(int l, int r, int mul, int add)
    {
        _modify(1, l, r, mul, add);
    }
	// 区间[l, r]的和
    int query(int l, int r)
    {
        return _query(1, l, r);
    }
private:
    // 由子结点信息更新父节点信息
    void pushup(int u)
    {
        tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
    }
    
    // 以mul add 更新结点t的懒标记
    void eval(Node& t, int mul, int add)
    {
        t.sum = t.sum * mul + add * (t.r - t.l + 1);
        t.mul *= mul;
        t.add = t.add * mul + add;
    }
	
    // 把父节点的懒标记传递到子结点
    void pushdown(int u)
    {
        eval(tr[u << 1], tr[u].mul, tr[u].add);
        eval(tr[u << 1 | 1], tr[u].mul, tr[u].add);
        tr[u].mul = 1, tr[u].add = 0;
    }

    // 建树
    void build(int u, int l, int r)
    {
        if (l == r)
        {
            tr[u] = {r, r, w[r], 1, 0};
            return;
        }
        tr[u] = {l, r, 0, 1, 0};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }

    // x in [l, r] x = x * mul + add的递归子函数
    void _modify(int u, int l, int r, int mul, int add)
    {
        if (tr[u].l >= l && tr[u].r <= r)
        {
            eval(tr[u], mul, add);
            return;
        }
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) _modify(u << 1, l, r, mul, add);
        if (r > mid) _modify(u << 1 | 1, l, r, mul, add);
        pushup(u);
    }
	// query的递归子函数
    int _query(int u, int l, int r)
    {
        if (tr[u].l >= l && tr[u].r <= r)
        {
            return tr[u].sum;
        }
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if (r <= mid) return _query(u << 1, l, r);
        if (l > mid) return _query(u << 1 | 1, l, r);
        return _query(u << 1, l, r) + _query(u << 1 | 1, l, r);
    }
	
    static const int N = 1e5 + 10;
    int w[N];
    Node tr[N * 4];
    int n;
};