知识回顾
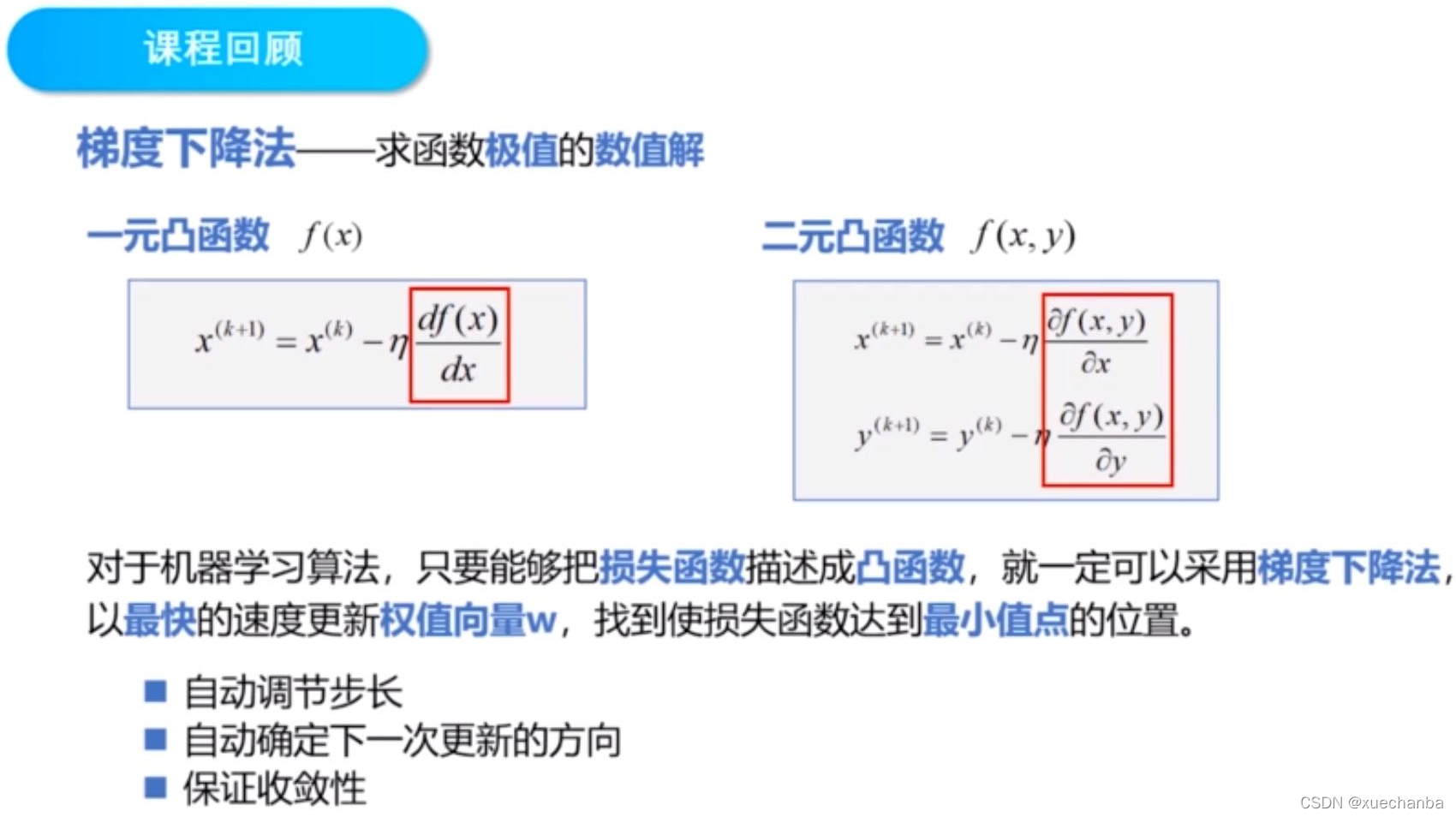
梯度下降法求解一元线性回归问题
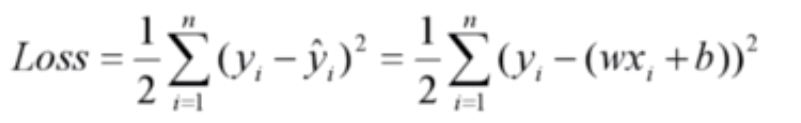
这是一元线性回归的平方损失函数,这里的样本点 x 和 y 都是已知的,变量是 w 和 b ,我们的目标是找到使损失函数达到最小值的 w 和 b。
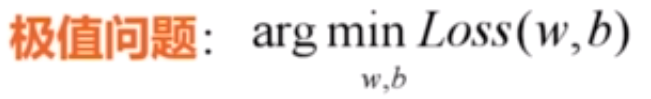
如果我们能够确定这个损失函数是一个凸函数,那么就可以使用梯度下降法来求解。
验证一元线性回归的平方损失函数是凸函数
把损失函数中的平方项展开,可以得到下图:
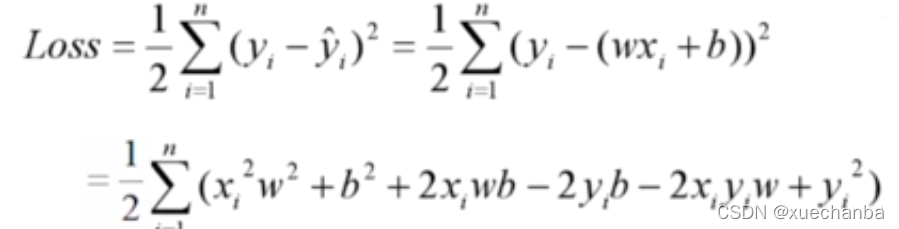
再把 ∑ 求和这一部分展开,并对 w2、w和b这些变量进行合并整理,分别提取公因式,系数用 A、B 、C、D、E 来表示,并将所有的常数项合并得到F,得到结果如下:
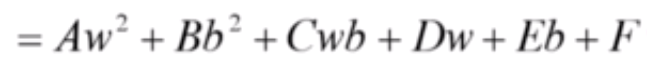
虽然我们不知道这个公式中的系数 A、B 、C、D、E 和 F 具体是什么值,但是我们可以先考察它的这个近亲函数:
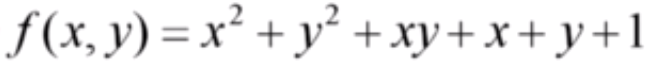
它的函数图像如下:
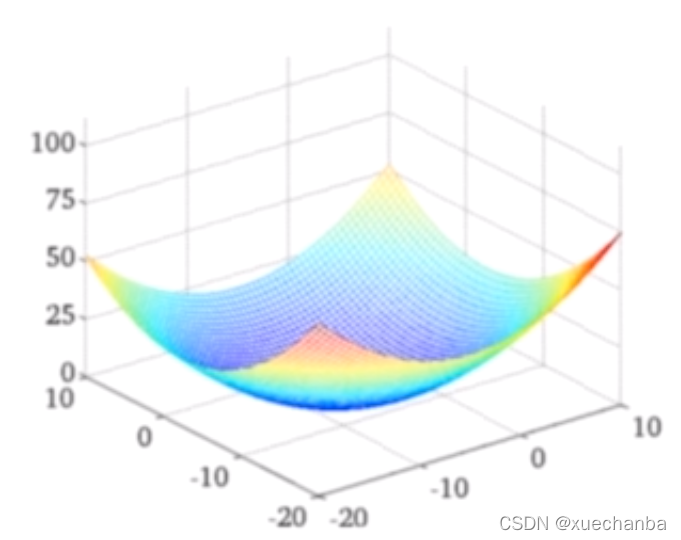
看上去像一个大碗,它显然是一个三维空间中的凸函数,因此求极值的问题,就是求解这个碗底的坐标。
总结:

这两个函数相比,只是系数不同,因此,可以确定这个一元线性回归的平方损失函数 Loss 也一定是一个凸函数。因此,它可以直接采用梯度下降法来求解。
推导一元线性回归的平方损失函数的迭代公式
这个平方损失函数是一个二元凸函数,变量是 w 和 b ,根据二元函数的梯度下降法,可以得到它的权值更新算法:
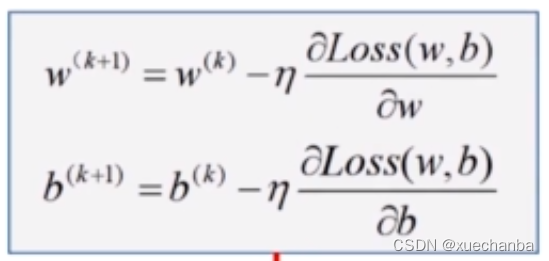
将 Loss 函数对 w 和 b 的偏导数
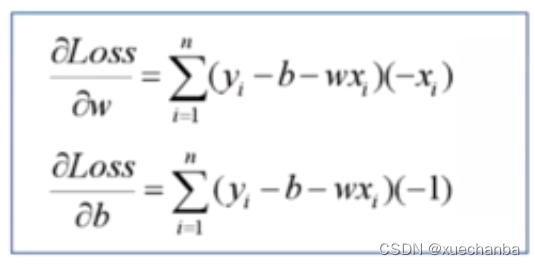
代入,就可以得到最终的迭代公式:
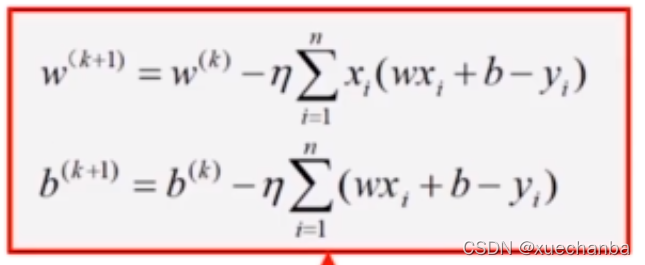
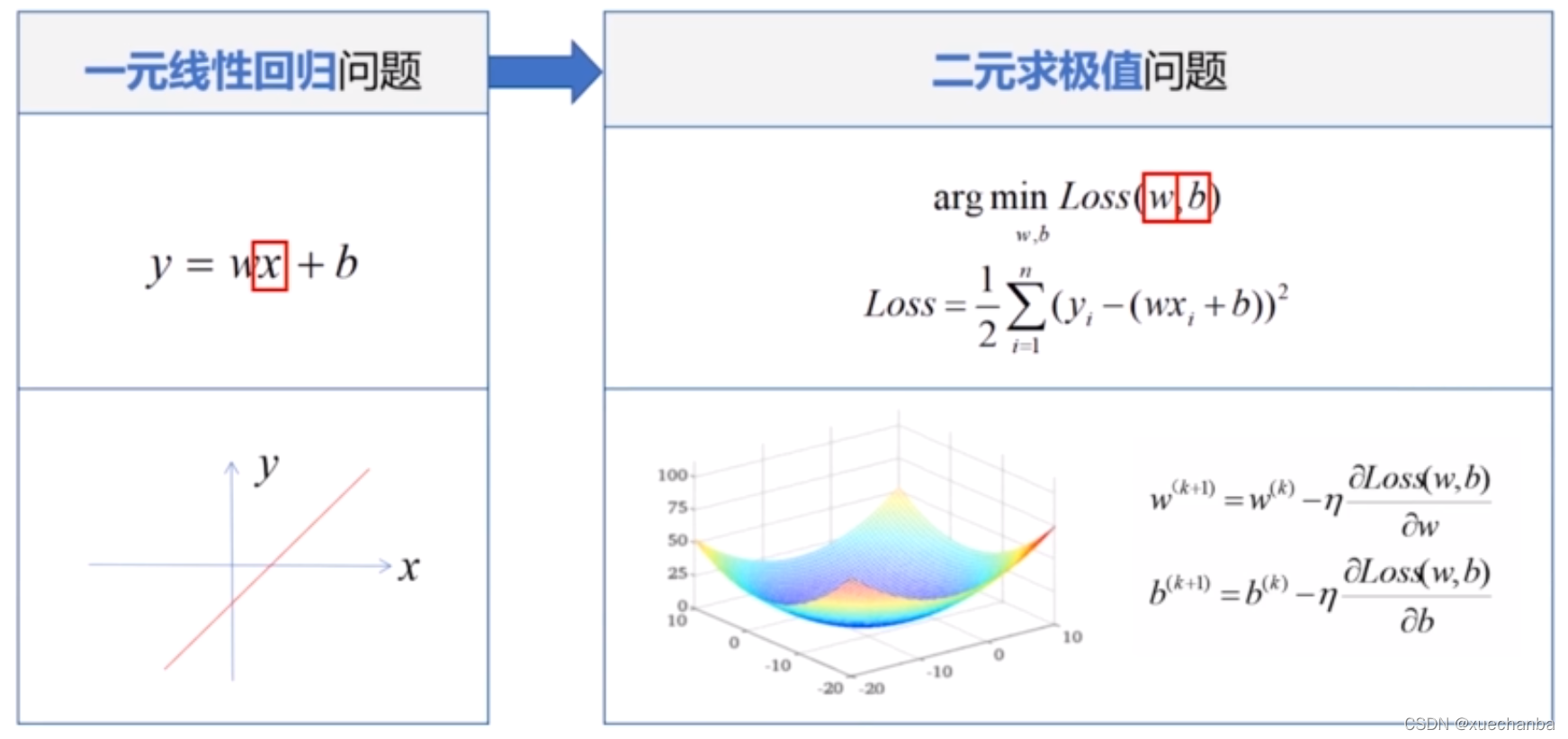
一元线性回归问题转化为二元求极值问题
一元线性回归中的一元是指自变量 x 只有一个,求解一元线性回归的问题就是损失函数求极值的问题。
它的损失函数中,有两个未知数,w 和 b,因此是二元函数。
一元线性回归可以用二维空间中的一条直线来表示,它的损失函数是三维空间中的一个凸函数。因为是凸函数,所以可以采用梯度下降法来求解。
一元线性回归的均方差损失函数

在编程中,我们经常使用均方差损失函数,均方差损失函数中的 n 是样本数量,它的模型参数更新算法在上图中也写出来了。
梯度下降法求解多元线性回归问题
使用梯度下降法求解一元线性回归的方法也可以被推广到求解多元线性回归问题。
这是多元线性回归的模型:
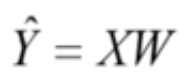
其中的 X 和 W 都是 m+1 维的向量。

下图为它的损失函数:
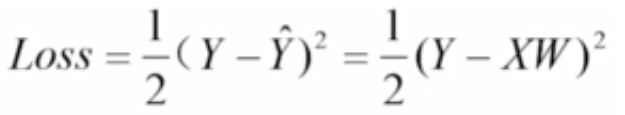
它也是一个高维空间中的凸函数,因此也可以使用梯度下降法来求解。
下图为它的权值更新算法:
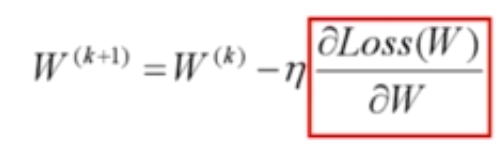
代入偏导数,
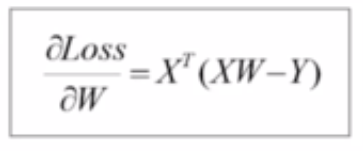
可以得到最终的迭代公式:
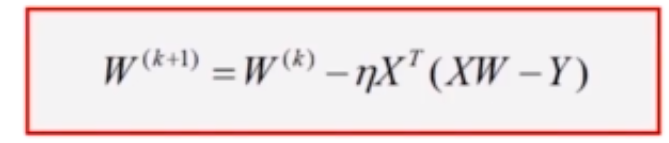
学习率
在梯度下降法中,学习率 η 是一个比较小的常数,
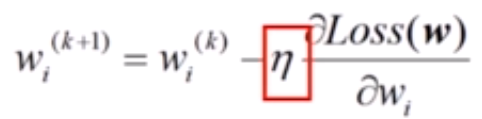
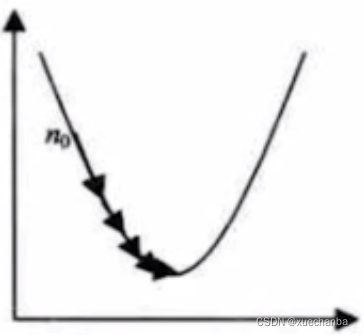
用来缓和每一步调整权值的程度,学习率越大,步长越大,学习率越小,步长也越小,从理论上来说,对于凸函数,只要学习率设置的足够小,就可以保证一定收敛。
但是,如果设置的过小,可能需要的迭代次数就非常多,训练的时间也就非常长,甚至一直达不到极值点。
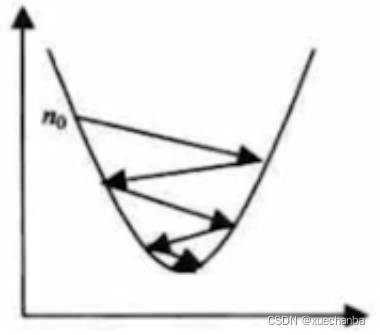
学习率设置的比较大,可能会产生振荡,在振荡中也可能慢慢收敛。
如果学习率设置的过大,那么就可能会产生严重振荡,导致系统无法收敛。
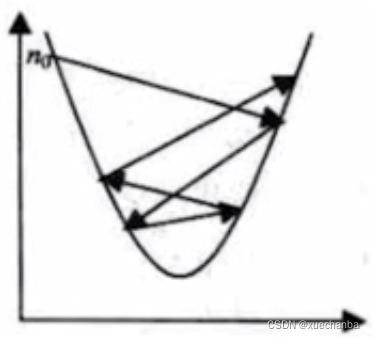
可见,学习率的选择非常的重要,既不能太大,也不能太小。我们可以根据经验来进行设置,也可以让它随着迭代次数的增加而逐渐衰减。
超参数的概念

学习率这个参数不是通过训练得到的,而是在开始学习之前就设置好的,这种参数也被称之为超参数。
选择一组好的超参数可以提高学习的性能和效果。
