7.1线性可分支持向量机和硬间隔最大化
7.1.1 线性可分支持向量机
给定线性可分训练集,通过间隔最大化或等价地求解相应的凸二次规划问题学习得到的分离超平面为
w
?
?
x
+
b
?
=
0
w^*\cdot x+b^*=0
w??x+b?=0
以及相应的分类决策函数
f
(
X
)
=
s
i
g
n
(
w
?
?
x
+
b
?
=
0
)
f(X)=sign(w^*\cdot x+b^*=0)
f(X)=sign(w??x+b?=0)
称为线性可分支持向量机。
7.1.2 函数间隔和几何间隔
首先要知道点到超平面 w ? x + b = 0 w\cdot x+b=0 w?x+b=0的距离 d = ∣ w ? x + b ∣ ∣ ∣ w ∣ ∣ d=\frac{|w\cdot x+b|}{||w||} d=∣∣w∣∣∣w?x+b∣?(推导见这里)
函数间隔为:
γ
^
i
=
y
i
(
w
?
x
i
+
b
)
{\hat{\gamma}}_i=y_i(w\cdot x_i+b)
γ^?i?=yi?(w?xi?+b)
所有样本点
(
x
i
,
y
i
)
(x_i,y_i)
(xi?,yi?)的函数间隔之间的最小值,即
γ
^
=
m
i
n
i
=
1
,
?
?
,
N
γ
^
i
\hat{\gamma}=\underset{i=1,\cdots ,N}{min}\hat{\gamma}_i
γ^?=i=1,?,Nmin?γ^?i?
函数间隔可以表示分类预测的正确性及确信度。但是选择分离超平面时, 只有函 数间隔还不够。因为只要成比例地改变
w
w
w 和
b
b
b, 例如将它们改为
2
w
2 w
2w 和
2
b
2 b
2b, 超平面并没有改变,但函数间隔却变成了原来的2倍。
γ
^
i
=
y
i
(
2
w
?
x
i
+
2
b
)
=
2
y
i
(
w
?
x
i
+
b
)
{\hat{\gamma}}_i=y_i(2w\cdot x_i+2b)=2y_i(w\cdot x_i+b)
γ^?i?=yi?(2w?xi?+2b)=2yi?(w?xi?+b),这一事实启示我们,可以对分离超平面的法向量
w
w
w加某些约束,如规范化,
∣
∣
w
∣
∣
=
1
||w||=1
∣∣w∣∣=1,这时函数间隔就变成了几何间隔。
γ
i
=
y
i
(
w
∣
∣
w
∣
∣
?
x
i
+
b
∣
∣
w
∣
∣
)
{\gamma}_i=y_i(\frac{w}{||w||}\cdot x_i+\frac{b}{||w||})
γi?=yi?(∣∣w∣∣w??xi?+∣∣w∣∣b?)
所有样本点
(
x
i
,
y
i
)
(x_i, y_i)
(xi?,yi?)的几何间隔的最小值,即
γ
=
m
i
n
i
=
1
,
?
?
,
N
γ
i
\gamma = \underset{i=1,\cdots ,N}{min}{\gamma}_i
γ=i=1,?,Nmin?γi?
当
∣
∣
w
∣
∣
=
1
||w||=1
∣∣w∣∣=1时,函数间隔和几何间隔相等,如果超平面参数
w
w
w和b成比例地改变(超平面并没有改变),函数间隔也按此比例改变,而几何间隔不变。
7.1.3 间隔最大化
最大间隔分离超平面的存在唯一性,存在性书上证明很容易看懂,下面来证明唯一性。
假设存在两个最优解 ( w 1 ? , b 1 ? ) (w^*_1,b^*_1) (w1??,b1??)和 ( w 2 ? , b 2 ? ) (w^*_2,b^*_2) (w2??,b2??)。显然 ∣ ∣ w 1 ? ∣ ∣ = ∣ ∣ w 2 ? ∣ ∣ = c ||w^*_1||=||w^*_2||=c ∣∣w1??∣∣=∣∣w2??∣∣=c,其中c是一个常数。令
w
=
w
1
?
+
w
2
?
2
,
b
=
b
1
?
+
b
2
?
2
w=\frac{w_{1}^{*}+w_{2}^{*}}{2}, b=\frac{b_{1}^{*}+b_{2}^{*}}{2}
w=2w1??+w2???,b=2b1??+b2???, 易知
(
w
,
b
)
(w, b)
(w,b) 也是解。
c
?
∣
∣
w
1
?
+
w
2
?
2
∣
∣
?
1
2
∣
∣
w
1
?
∣
∣
+
1
2
∣
∣
w
2
?
∣
∣
=
c
c\leqslant ||\frac{w^*_1+w^*_2}{2}||\leqslant \frac{1}{2}||w^*_1||+\frac{1}{2}||w^*_2||=c
c?∣∣2w1??+w2???∣∣?21?∣∣w1??∣∣+21?∣∣w2??∣∣=c
所以
∣
∣
w
∣
∣
=
1
2
∣
∣
w
1
?
∣
∣
+
1
2
∣
∣
w
2
?
∣
∣
||w||=\frac{1}{2}||w^*_1||+\frac{1}{2}||w^*_2||
∣∣w∣∣=21?∣∣w1??∣∣+21?∣∣w2??∣∣,因此
w
1
?
=
λ
w
2
?
,
∣
λ
∣
=
1
w^*_1=\lambda w^*_2, |\lambda|=1
w1??=λw2??,∣λ∣=1,若
λ
=
?
1
,
则
w
=
0
\lambda=-1,则w=0
λ=?1,则w=0不符合题意,所以
w
1
?
=
w
2
?
w^*_1=w^*_2
w1??=w2??。下面再证
b
1
?
=
b
2
?
b^*_1=b^*_2
b1??=b2??。设
x
1
′
x_{1}^{\prime}
x1′? 和
x
2
′
x_{2}^{\prime}
x2′? 是集合
{
x
i
∣
y
i
=
+
1
}
\left\{x_{i} \mid y_{i}=+1\right\}
{xi?∣yi?=+1} 中分别对应于
(
w
?
,
b
1
?
)
\left(w^{*}, b_{1}^{*}\right)
(w?,b1??) 和
(
w
?
,
b
2
?
)
\left(w^{*}, b_{2}^{*}\right)
(w?,b2??) 使得问题的不等式等号成立的点,
x
1
′
′
x_{1}^{\prime \prime}
x1′′? 和
x
2
′
′
x_{2}^{\prime \prime}
x2′′? 是集合
{
x
i
∣
y
i
=
?
1
}
\left\{x_{i} \mid y_{i}=-1\right\}
{xi?∣yi?=?1} 中分别对应于
(
w
?
,
b
1
?
)
\left(w^{*}, b_{1}^{*}\right)
(w?,b1??) 和
(
w
?
,
b
2
?
)
\left(w^{*}, b_{2}^{*}\right)
(w?,b2??) 使得问题的不等式等号成立的点。
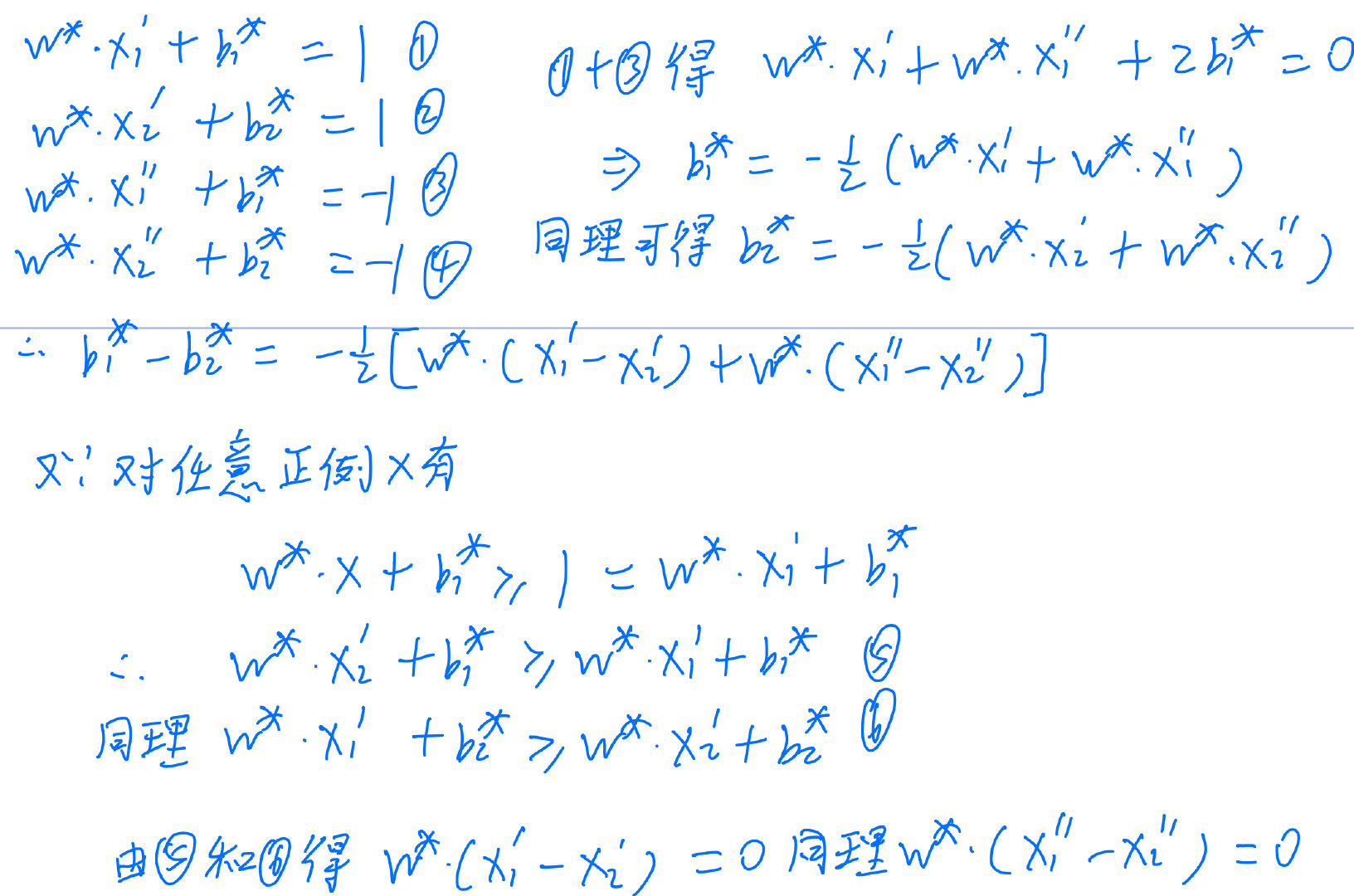
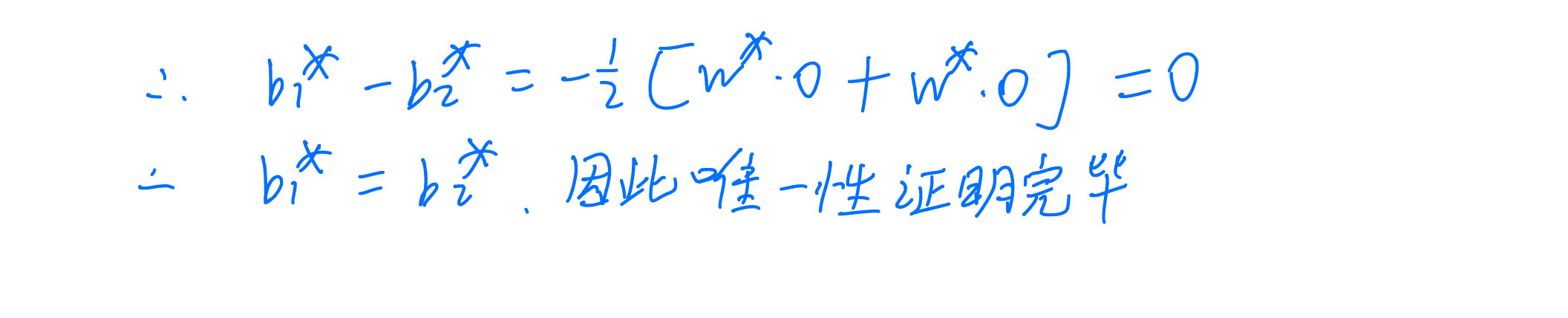
7.1.4 学习的对偶算法
下面是对拉格朗日函数的一个补充解释

下面是对(7.28)式的补充解释

7.3 非线形支持向量机和核函数
证明运算*是空间S的内积的补充



7.4 序列最优最小化算法
以下是对 α 2 \alpha_{2} α2?的取值范围进行的推导


补充 α 2 n e w \alpha_{2}^{new} α2new? 怎么得到 α 1 n e w \alpha_{1}^{new} α1new?
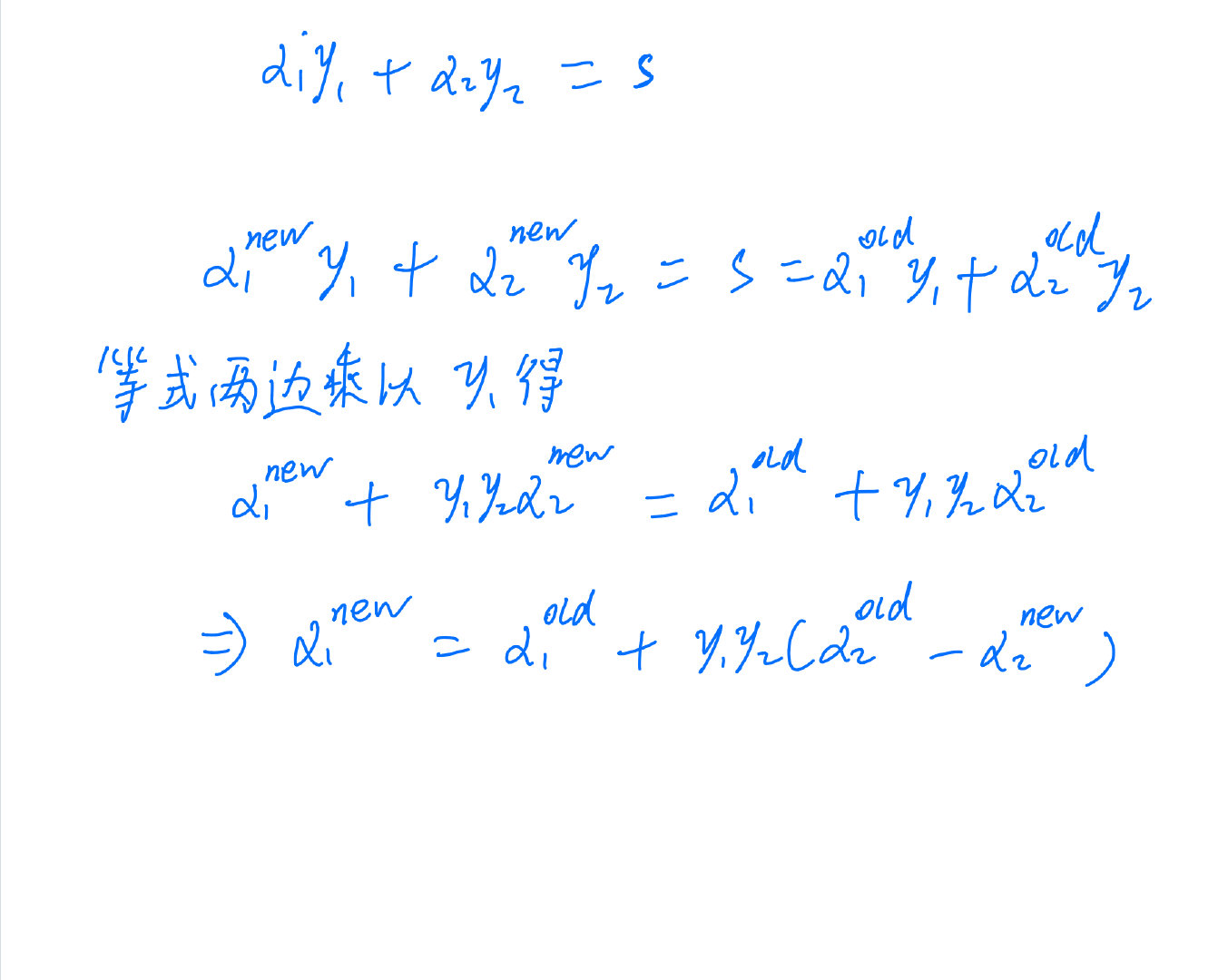
7.4.2 变量的选择
关于SMO算法中第一个变量的选择的KKT条件的补充,可以看这个博客,下面是我自己对博客中的内容进行了优化,建议两个结合起来看。
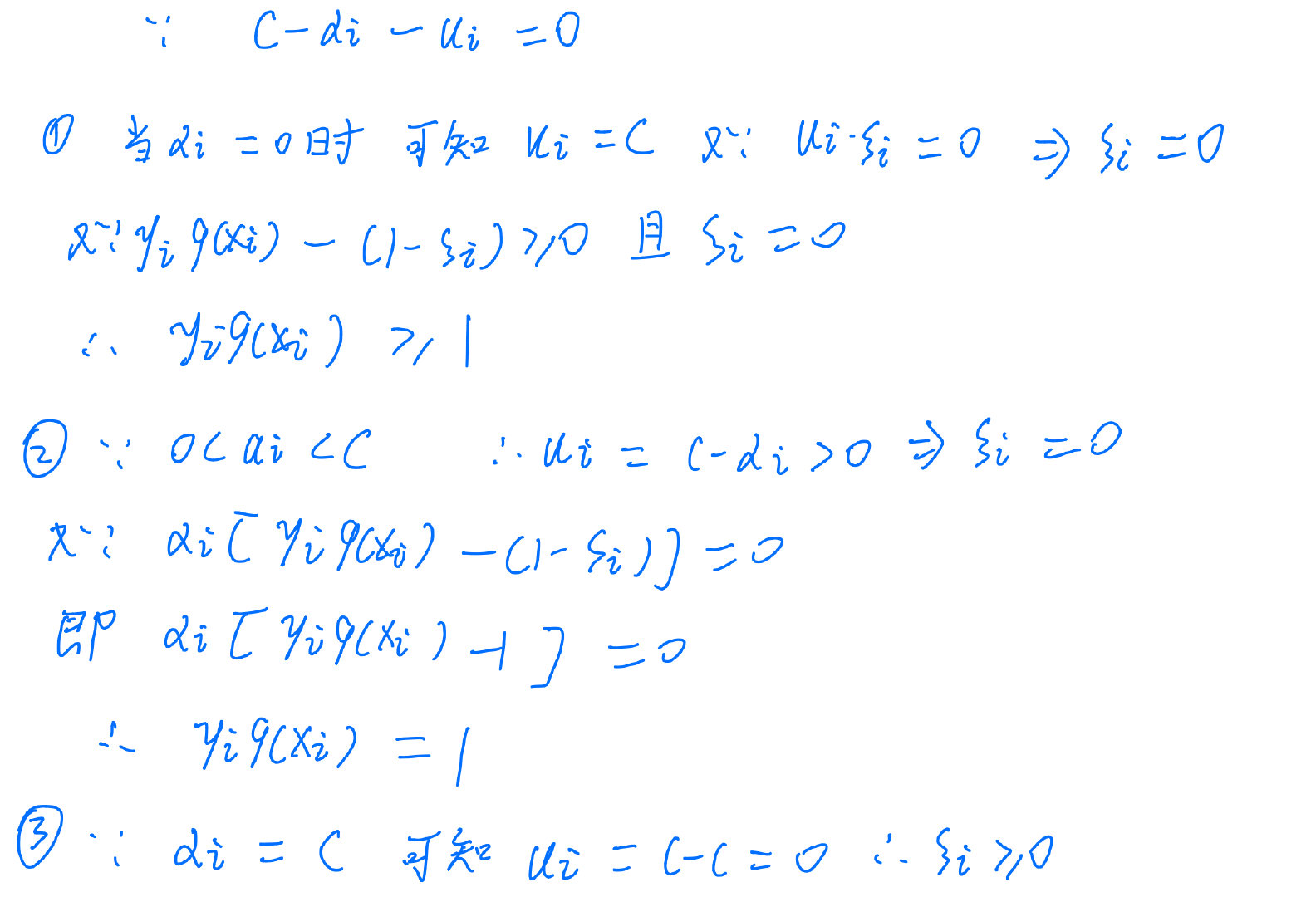
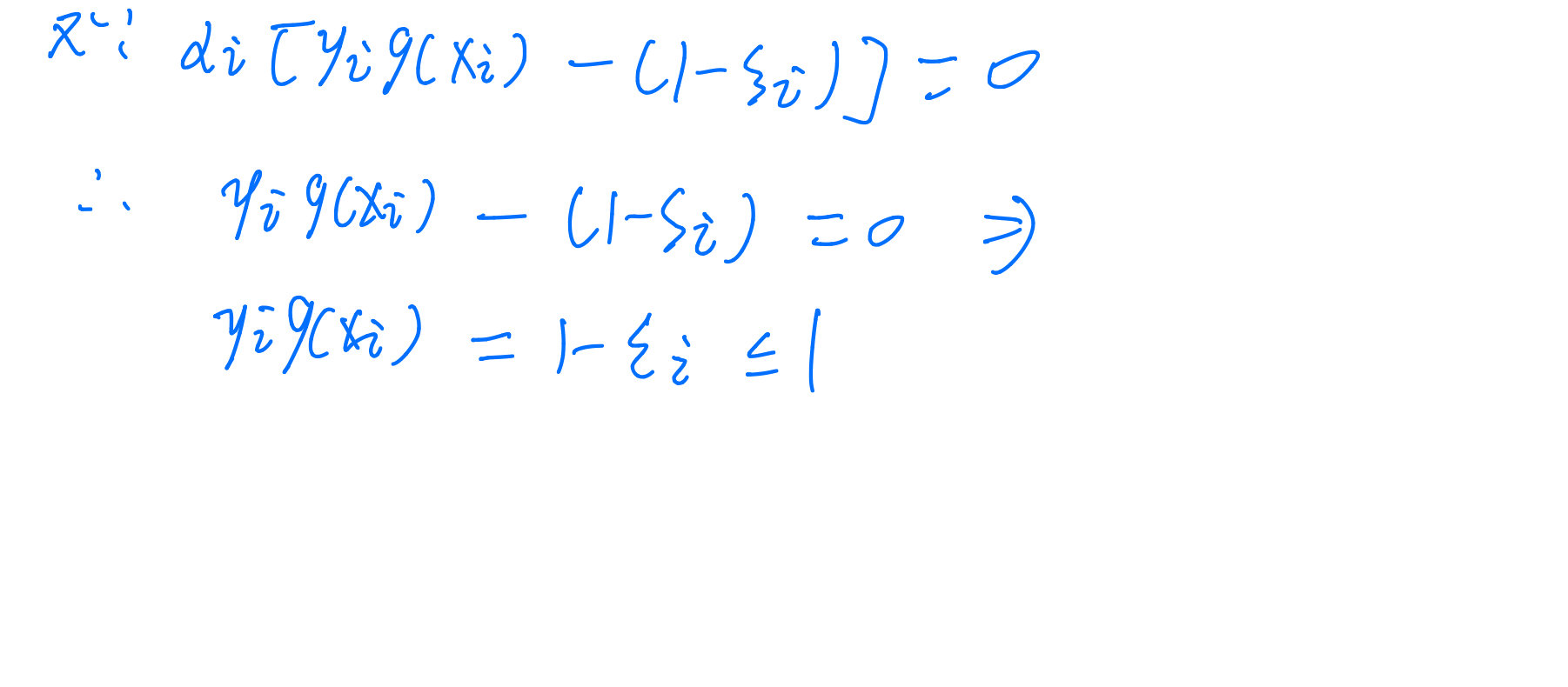
参考:
