1 概述
1.1 皮尔逊Ⅲ型分布(P-Ⅲ型分布)
皮尔逊Ⅲ型曲线是一条一端有限、一端无限的不对成单峰曲线,数学上称Gamma分布。
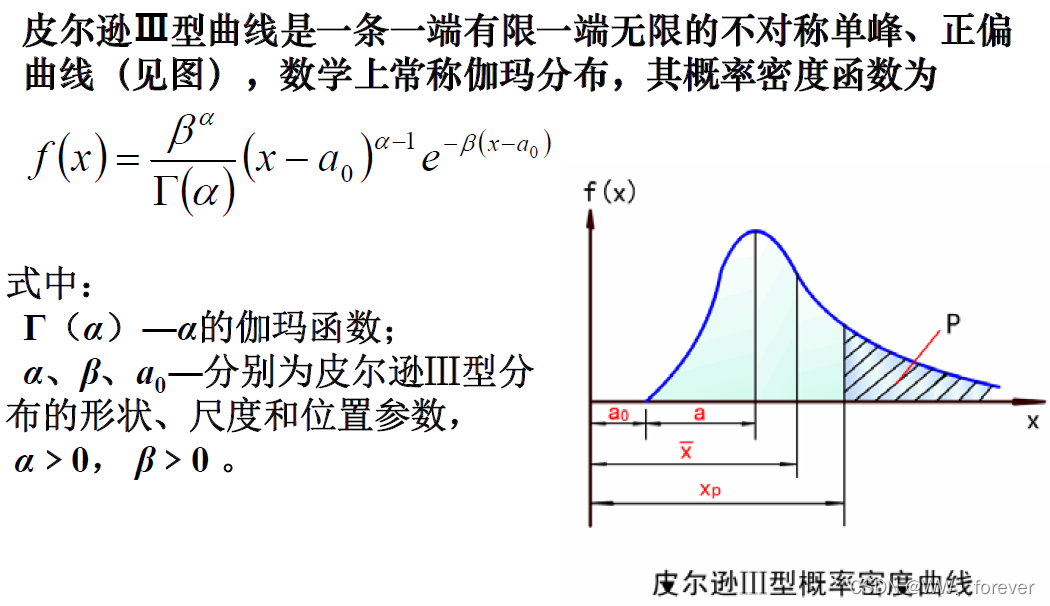

1.2 参数估计
1.2.1 矩法

1.2.2 三点法


1.2.3 权函数法

1.2.4 概率权重法

1.3 重点问题
Gamma分布取值必须大于0,但对于P-Ⅲ型分布而言,取值可以为负。
2 MATLAB代码实现
2.1 参数拟合
根据矩法求得皮尔逊Ⅲ型分布的三个参数。
MATLAB代码如下:
% 函数1:fitP3函数用于拟合得到皮尔逊Ⅲ型分布的三个参数
% ------------------------------------------------------------------
function [alpha , beta , a0] = fitP3( X )
% alpha 形状参数
% beta 尺度参数
% a0 位置参数
if isvector(X)
n = length(X);
else
error("输入数据并非向量!")
end
Xmean = mean(X); % 计算样本X的均值
K = X/Xmean; % 计算模比系数K
Cv = sqrt((1/(n-1)).*sum((K-1).^2)); % 计算变差系数Cv
Cs = (sum((K-1).^3))/(Cv^3)/(n-3); % 计算偏态系数Cs
alpha = 4/(Cs^2); % P3分布参数:形状参数计算>0
beta = 2/(Xmean*Cv*abs(Cs)); % P3分布参数:尺度参数计算>0
a0 = Xmean-2*Cv*Xmean/Cs; % P3分布参数:位置参数计算
end
2.2 密度函数
MATLAB代码如下:
% 函数2:P3pdf函数用于得到相应密度函数
% ------------------------------------------------------------------
function P = P3pdf( X , alpha , beta , a0 )
% 利用P3分布得到相应密度函数
if isvector(X)
n = length(X);
else
error("输入数据并非向量!")
end
X=X(:);
Xmean = mean(X); % 计算样本X的均值
K = X/Xmean; % 计算模比系数K
Cv = sqrt((1/(n-1)).*sum((K-1).^2)); % 计算变差系数Cv
Cs = (sum((K-1).^3))/(Cv^3)/(n-3); % 计算偏态系数Cs
Y =zeros(n,1);
if Cs>0
Y = X-a0;
else
Y = a0-X;
end
P =zeros(n,1);
for in=1:n
P(in,1) = beta^alpha/gamma(alpha)*Y(in,1)^(alpha-1)*exp( -beta* Y(in,1) );
% P(in,1) = gampdf( X(in,1)-a0 ,alpha,1/beta);
end
% 与Gamma分布进行比较
% PP = gampdf(X-a0 ,alpha , 1/beta );
end
2.3 分布函数
MATLAB代码如下:
% 函数3:P3cdf函数用于得到相应分布函数(三变量Gamma分布)
% ------------------------------------------------------------------
function P = P3cdf( X , alpha , beta , a0 )
% 利用P3分布得到相应分布函数
if isvector(X)
n = length(X);
else
error("输入数据并非向量!")
end
X=X(:);
Xmean = mean(X); % 计算样本X的均值
K = X/Xmean; % 计算模比系数K
Cv = sqrt((1/(n-1)).*sum((K-1).^2)); % 计算变差系数Cv
Cs = (sum((K-1).^3))/(Cv^3)/(n-3); % 计算偏态系数Cs
if Cs>0
Y = X-a0;
else
Y = a0-X;
end
Y = max(Y,0); % Y<0则取值为0
if Cs>0
P= gammainc(Y*beta,alpha,'lower');
else
P= 1- gammainc(Y*beta,alpha,'lower');
end
% 与Gamma分布进行比较
% PP = gamcdf(X-a0 ,alpha , 1/beta );
end
3 示例
MATLAB代码如下:
clc
close all
clear
%%
load('X.mat');
[alpha , beta , a0] = fitP3( X );
Xpdf = P3pdf( X , alpha , beta , a0 );
Xcdf = P3cdf( X , alpha , beta , a0 );
