每日算法题
csdn算法技能树,基础1-5
1.切面条
一根高筋拉面,中间切一刀,可以得到2根面条。
如果先对折1次,中间切一刀,可以得到3根面条。
如果连续对折2次,中间切一刀,可以得到5根面条。
那么,连续对折10次,中间切一刀,会得到多少面条呢?
tips: 这题,看一眼答案就会了。但不懂如何找这种规律,推了几次都不对,或许这种得多做看经验吧。
答案(golang实现):
n, sum, t := 10, 2, 1
for i := 1; i < n; i++ {
sum += t
t *= 2
}
fmt.Printf("对折10次会得到%d个面条", sum)
// 折10次会得到513个面条
2.大衍数列
中国古代文献中,曾记载过
大衍数列, 主要用于解释中国传统文化中的太极衍生原理。它的前几项是:0、2、4、8、12、18、24、32、40、50 …
其规律是:对偶数项,是序号平方再除2,奇数项,是序号平方减1再除2。
代码打印出大衍数列的前 100 项。
通过i%2是否为零来判断奇偶。余2为0则i项为i*i/2,否则为:(i*i-1)/2
答案(golang实现):
for i := 1; i < 100; i++ {
if i&2 == 0 {
fmt.Printf("第%d项为:%d", i, i*i/2)
} else {
fmt.Printf("第%d项为:%d", i, (i*i-1)/2)
}
}
3.门牌制作
小蓝要为一条街的住户制作门牌号。
这条街一共有 2020 位住户,门牌号从 1 到 2020 编号。
小蓝制作门牌的方法是先制作 0 到 9 这几个数字字符,最后根据需要将字符粘贴到门牌上,例如门牌 1017 需要依次粘贴字符 1、0、1、7,即需要 1 个字符 0,2 个字符 1,1 个字符 7。
请问要制作所有的 1 到 2020 号门牌,总共需要多少个字符 2?
tips: 拿到一个门牌号后,直接余10可以得到最后一位树,如果等于2,所需字符加一。每次除10舍掉最后一位,直到拆解完所有位(门牌号被除的小于0)
答案(golang实现):
count := 2020
ans := 0
for i := 1; i <= count; i++ {
x := i
for x > 0 {
if x%10 == 2 {
ans++
}
x /= 10gg
}
}
fmt.Printf("要制作所有的 1 到 2020 号门牌,总共需要%d个字符 2", ans)
// 要制作所有的 1 到 2020 号门牌,总共需要624个字符 2
4.方阵转置
给定一个n×m矩阵相乘,求它的转置。其中1≤n≤20,1≤m≤20,矩阵中的每个元素都在整数类型(4字节)的表示范围内。
tips: 即方阵顺时针旋转90度。x轴反向和y轴方向倒换
m, n := 20, 20
var a [20][20]int
// 初始化方阵
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
a[i][j] = j
}
}
fmt.Print("原数组")
fmt.Println(a)
fmt.Println("反转后")
// 转置方阵
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
fmt.Print(a[j][i])
}
// 换个行
fmt.Println()
}
5.微生物增殖
假设有两种微生物 X 和 Y
X出生后每隔3分钟分裂一次(数目加倍),Y出生后每隔2分钟分裂一次(数目加倍)。
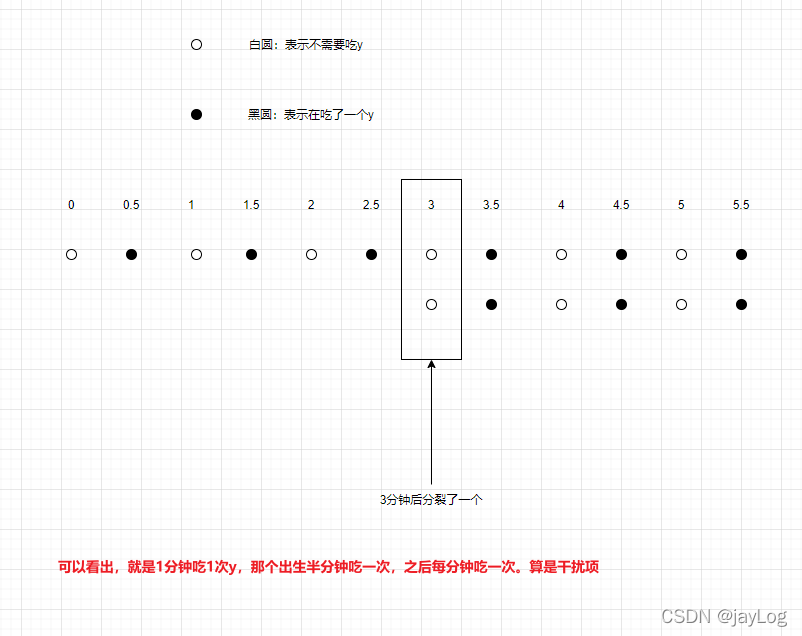
一个新出生的X,半分钟之后吃掉1个Y,并且,从此开始,每隔1分钟吃1个Y。
现在已知有新出生的 X=10, Y=89,求60分钟后Y的数目。
如果X=10,Y=90呢?
提示:
分析可知,Y分别会在0.5,1.5,2.5······时被吃,所以,把60分钟分成120份,则在除以2余数为1时,Y的数目减少X个
tips:一个新出生的X,半分钟之后吃掉1个Y,并且,从此开始,每隔1分钟吃1个Y。这句话其实算干扰项了。这里我思索了很久,画图一看便知。其他条件比较简单,直接余即可
缩小一下研究对象,看看如果 只有一个x的情况 。如下:
答案(golang实现):
func demo5func(x, y int) {
fmt.Printf("x=%d,y=%d,60分钟后,y的数目为:", x, y)
for i := 0; i < 120; i++ {
if i%2 == 1 {
y -= x
}
if i%4 == 0 {
y *= 2
}
if i%6 == 0 {
x *= 2
}
}
fmt.Println(y)
}
demo5func(10, 89)
demo5func(10, 90)
/*
x=10,y=89,60分钟后,y的数目为:-979369984
x=10,y=90,60分钟后,y的数目为:94371840
*/
