题目
- 在 n x n 的网格 grid 中,我们放置了一些与 x,y,z 三轴对齐的 1 x 1 x 1 立方体。
- 每个值 v = grid[i][j] 表示 v 个正方体叠放在单元格 (i, j) 上。
现在,我们查看这些立方体在 xy 、yz 和 zx 平面上的投影。
投影 就像影子,将 三维 形体映射到一个 二维 平面上。从顶部、前面和侧面看立方体时,我们会看到“影子”。- 返回 所有三个投影的总面积 。
示例1 :
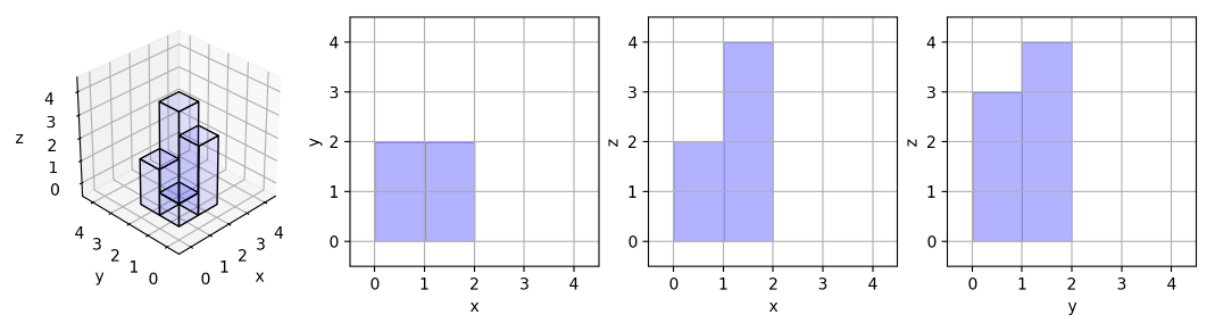
输入:[[1,2],[3,4]]
输出:17
解释:这里有该形体在三个轴对齐平面上的三个投影(“阴影部分”)。
示例2
输入:[[1,0],[0,2]]
输出:8
示例3
输入:grid = [[2]]
输出:5
我的答案
-
这个题是什么意思呢 :
grid是一个二维数组 ,
把第二层数组里面的数换成1*1*1的正方体 , 数字是几就向z轴落几个正方体
一行一行的摆放
然后在x-y-z坐标系里就有了投影
分别求向面xy , 面xz , 面yz 投影的面积 , 返回三者之和 -
解题思路 :
-
面xy 投影面积 :
我的写法是 ;grid[i].length相加 再去除grid[i][j] === 0 时
解释 :grid[i].length就是每一行在网格上占的格数 , 让他们相加 , 同时考虑第二层数等于零的情况 , 当grid[i][j] === 0时 , 面积和减一 , 即可得到面xy投影面积 -
面xz投影面积
我的写法是 : 取Math.max.apply(null, grid[i])相加(这一篇里有apply函数的用法解释)
解释 : 让每一行里面的最大数相加 , 即可得到面xz投影面积 -
面yz投影面积
我的写法是 : 取grid[j][i]里面的最大值 , 让最大值相加
解释 : 前面都是横着看的 , 对于面yz要竖着看 , 所以是grid[j][i], 依旧是最大值相加 , 即可得到面yz投影面积
-
-
代码 :
/**
* @param {number[][]} grid
* @return {number}
*/
var projectionArea = function(grid) {
let Sxy = 0
let Sxz = 0
let Syz = 0
// 求面xy投影面积
for (let i = 0; i < grid.length; i++) {
Sxy += grid[i].length
for (let j = 0; j < grid[i].length; j++) {
if (grid[i][j] === 0) {
Sxy--
}
}
}
//求面xz和yz投影面积
for (i in grid) {
Sxz += Math.max.apply(null, grid[i])
SyzHeight = 0
for (j in grid[i]) {
SyzHeight = Math.max(grid[j][i], SyzHeight)
}
Syz += SyzHeight
}
let s = Sxy + Sxz + Syz
return s
};
