冒泡排序(稳定 O(n^2))
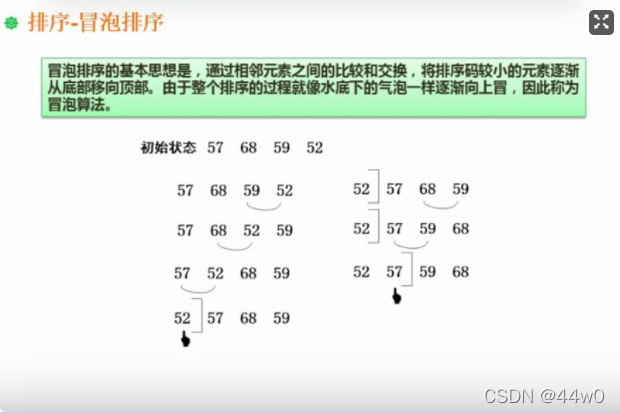
通过相邻元素之间的比较和交换,将排序码小的元素逐渐从底部移向顶部。
// 冒泡,相邻元素之间比较
function fn(arr){
for(let i=0;i<arr.length-1;i++){
for(let j=0;j<arr.length-1-i;j++){
if(arr[j]>arr[j+1]){
let temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
return arr;
}
let arr = [57, 68, 59, 52, 72, 28, 96, 33, 24, 19];
console.log(fn(arr));
快速排序(不稳定 O(nlogn))

找基准,比基准大的放右边,比基准小的放左边。
function fn(arr){
if(arr.length<=1) return arr;
let index= Math.floor(Math.random()*arr.length);
let left =[];
let right = [];
for(let i=0;i<arr.length;i++){
if(arr[i]<=arr[index]){
left.push(arr[i]);
}else {
right.push(arr[i]);
}
}
return fn(left).concat(fn(right))
}
let arr =[57,68,59,52,72,28,96,33,24,19];
console.log(fn(arr));
归并排序(稳定 O(nlogn))

分治:
- 先将数组分成一半,把左边的排序,右边的排序,之后再归并在一起。
- 左边和右边的数组进行排序,将左边和右边的数组看作单独的一个数组,继续划分。
- 直到每个部分只有一个元素了,不需要再排序了,直接归并就可以。
- 归并到上一个层级之后继续归并,归并到更高的层级,直到归并完成。
//拆分
function fn(arr){
if(arr.length<2) return arr;
let mid = parseInt(arr.length/2);
let left = arr.slice(0,mid);
let right = arr.slice(mid);
return fn2(fn(left),fn(right));
}
// 排序+归并
function fn2(left,right){
let res =[];
// 比大小,拿每个数组中第一个最小的
while(left.length>0&&right.length>0){
if(left[0]<right[0]){
res.push(left.shift());
}else{
res.push(right.shift());
}
}
// 跳出循环,left或者right会有一个还有数字
return res.concat(left).concat(right);
}
let arr =[57,68,59,52,72,28,96,33,24,19];
console.log(fn(arr));
插入排序(稳定 O(n^2))

移动法:
在新数字插入过程中,与前面的数字不断比较,前面的数字不断向后挪出位置,当新数字找到自己的位置后,插入一次即可。(从无序的数组中取出一个数字,与有序列表中的最后一个对比,如果小于,就将有序列表中的数字向后移动,直到找到该数组的合适位置。)
function fn(arr){
if(arr.length<2) return arr;
for(let i=1;i<arr.length;i++){
let j = i-1;
// 需要记录一下当前arr[i]的值,进入while循环时会改变当前值
let item = arr[i];
while(j>0&&item<arr[j]){
arr[j+1] =arr[j];
j--;
}
arr[j+1] = item;
}
return arr;
}
let arr =[57,68,59,52,72,28,96,33,24,19];
console.log(fn(arr));
希尔排序(不稳定 O(nlogn))
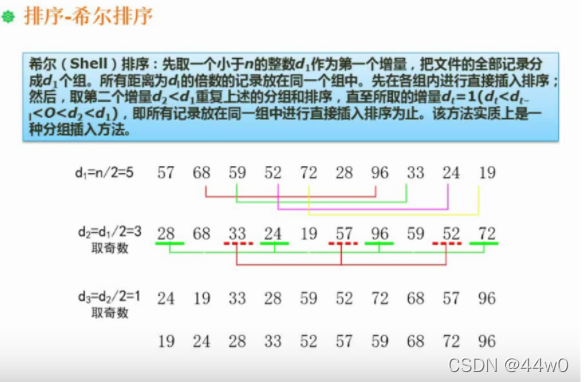
插入排序的一种,直接插入排序的优化:
先进行分组,再分别对每组进行直接插入排序,继续分组,继续排序,直到分组到一个元素为一组,结束
function fn(arr) {
//分组
let gap = Math.floor(arr.length / 2);
while (gap >= 1) {
for (let i = gap; i < arr.length; i++) {
let j = i - gap;
let item = arr[i];
while (j >= 0 && item < arr[j]) {
arr[j + gap] = arr[j];
j = j - gap;
}
arr[j + gap] = item;
}
gap = Math.floor(gap / 2);
}
return arr;
}
let arr = [57, 68, 59, 52, 72, 28, 96, 33, 24, 19];
console.log(fn(arr));
直接选择排序(不稳定 O(n^2))

双重循环遍历数组:
每经过一轮比较,找到最小元素的下标,将其交换至首位。(每一轮排序都找出当前的最小值,把这个最小值交换至本轮首位。)
function fn(arr){
let minIndex ;
//确定最小值的下标
for(let i=0;i<arr.length;i++){
minIndex = i;
for(let j=i+1;j<arr.length;j++){
if(arr[j]<arr[minIndex]){
minIndex = j;
}
}
//交换
let temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
return arr;
}
let arr =[57,68,59,52,72,28,96,33,24,19];
console.log(fn(arr));
堆排序 (不稳定 O(nlogn))

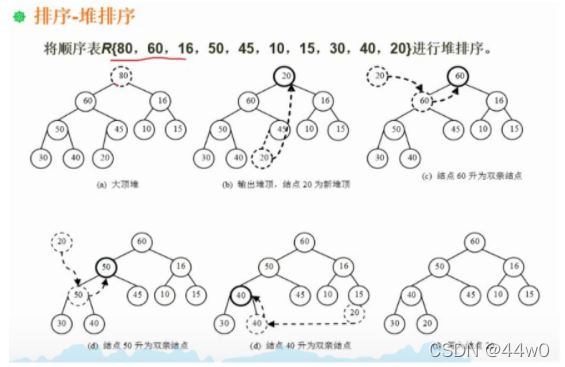
思路:先进行初建堆,再进行堆排序,继续执行前面操作
- 根据给出的序列,建立一个完全二叉树
- 进行调整,从最后一个非叶子结点,该节点是否全大于该子节点,如果有子节点大于该节点,双方交换,一次进行到根节点,如果下边又出现了该情况,则继续进行交换。—此时初建堆完成
- 进行堆排序:将根节点从树中去掉,把最后一个结点放到根节点,再进行初建堆的初始化步骤,循环该操作,直到所有节点从树中移除
//堆排序
function fn(arr){
// 初始化大堆顶,从第一个非叶子节点开始
// 完全二叉树中,父节点是i时,左孩子为2i+1,右孩子是2i+2
let index = Math.floor(arr.length/2-1);
// 先建立大根堆,向上比较的过程,进来的元素与父元素比较,大了就向上走
for(let i=index;i>=0;i--){
fn1(arr,i,arr.length);
}
// 大根堆此时已经建立好,将根节点从树中去掉,
// 把最后一个结点放到根节点,再进行初建堆的初始化步骤,循环该操作,直到所有节点从树中移除
// 次循环就是把跟顶元素,也就是数组中的第一个元素和最后一个元素进行交换,继续进行堆排序
for(let j=arr.length-1;j>0;j--){
const temp = arr[0];
arr[0] = arr[j];
arr[j] = temp;
fn1(arr,0,j);
}
return arr;
}
//将i节点以下整理成大堆顶
function fn1(arr,i,length){
// 完全二叉树中,父节点是i时,左孩子为2i+1,右孩子是2i+2
for(let j=2*i+1;j<length;j=2*j+1){
const temp = arr[i];
// 判断右孩子节点和左孩子节点哪一个更大,直接拿最大的节点和改父节点比较就可以
if(j+1<length&& arr[j]<arr[j+1]){
j++;
}
// 如果孩子中的最大节点大于根节点就进行交换,不大于的话不做处理
if(temp<arr[j]){
arr[i]=arr[j];
arr[j]=temp;
i=j;
}else break;
}
}
let arr = [57, 68, 59, 52, 72, 28, 96, 33, 24, 19];
console.log(fn(arr));
