时间复杂度+稳定性+思想
时间复杂度
稳定性

稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的
假设
有数组{2,3,A7,B7,9,10,4}进行升序的排序 排序后的数组{2,3,4,B7,A7,9,10};我们可以发现此时B7在A7的后面,那么就说这个排序是不稳定的!
稳定性的意义:格局打开,有时候我们排序的不仅仅是数字,可能是一个结构体,或者是其他,例如:我们排序的是高考成绩,首先比较两个人的总分,若总分相同,理工科比较的是数学,数学高的排名靠前,如果数学相同,再比较其他学科,这时候如果我们使用的排序是不稳定的,那么在分数相同的时候,数学低的那个同学反而排名有可能靠前。所以一个稳定的排序在日常使用中很重要!因为我们这个时候可以先按数学排序,然后再按总分排序。还有:假设一次奥数比赛中,不仅比正确率,还比时间,A和B两位选手,分数一样,但是A花了100分钟,但是B花了150分钟,这个时候也可以比较
总结:排序的时候只要隔着元素交换或者隔着元素插入,那么这个排序就可以说是不稳定的!

比较排序
直接插入排序的思想+时间复杂度及稳定性

思想
当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移

时间复杂度
最坏的情况是每次插入的第i个数字都是最小的数字,那么其每次都得和前面的i-1个数字比较,那么比较的总次数就是:1+2+3+…+i-1
此时的时间复杂度就是O(N^2)
最好的情况每次直接插入的数字都是最大的数字,那么每次只需要比较一次就可以了,那么此时的时间复杂度就是O(N);
稳定性:根据我们的实现思想可知,每次交换都是两个相邻的数字交换,那么该排序算法是稳定的。
总结我们使用直接插入排序的时候,当需要排序的数组约有序,那么所需要耗费的时间越少,因为我们每次都是从最后一个数字开始比较的
直接插入排序实现

void InsertSort(int* a, int n)//插入排序
{
for (int i = 0; i < n-1; i++)
{
int end = i;
int tam = a[end+1];//每次从i+1开始插入
while (end>=0)
{
if (tam < a[end])
{
a[end + 1] = a[end];
end--;
}
else
break;
}
a[end + 1] = tam;
//当插入的数字是最小的时候此时end跳出循环时候值是-1
//所以都要写成a[end+1] = tam
}
}
希尔排序的思想+时间复杂度及稳定性

思想希尔排序可以说是直接插入排序的优化版本。从上述直接插入排序的讨论可以知道,数组有序性越高,那么排序所需耗费的时间越少,所以,当随机给我们一串数组的时候,我们如果可以有一个操作使得需要排序的数组有序性增高,那么之后再进行直接插入排序所耗费的时间便减少了。因此希尔排序可以分成两步:
1,预处理
2,直接插入排序
如何进行预处理:
我们将数组分成几个组,取gap为间隔的值,然后先将每组进行直接插入排序。
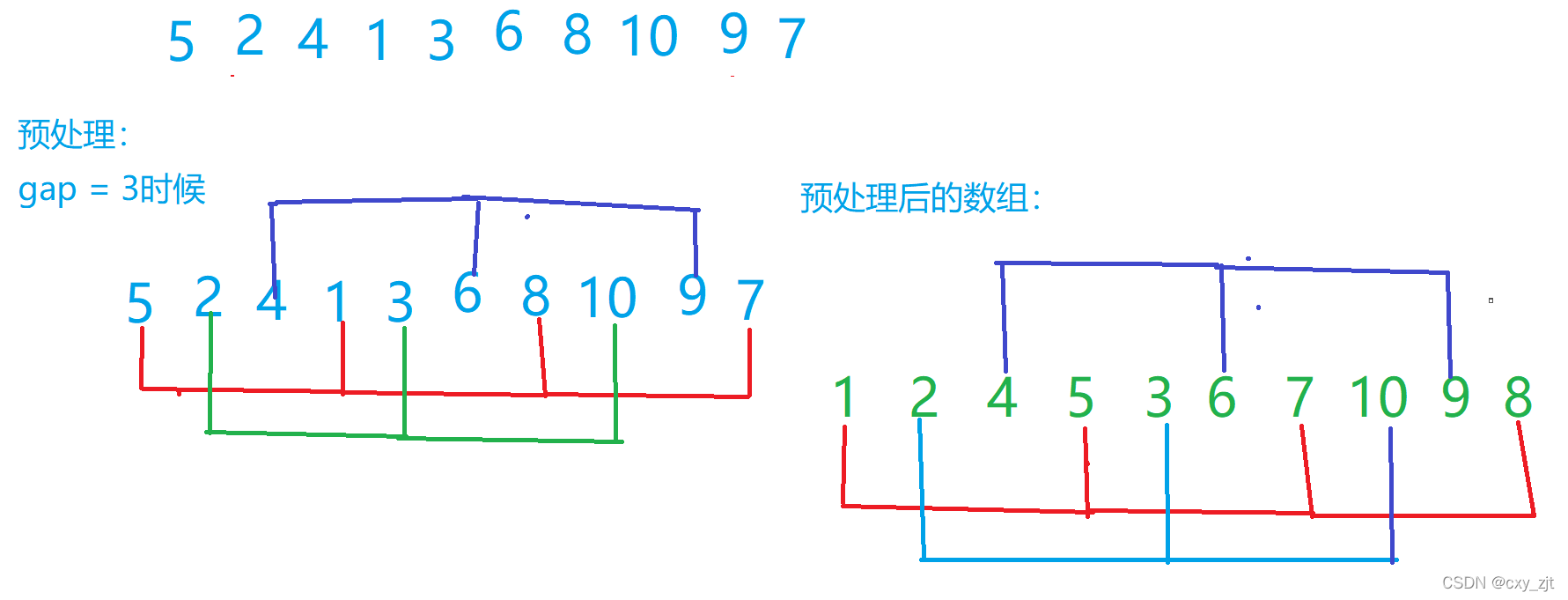
为什么这样做可以减少排序时间?
因为不管如何排序,较大的数字一定在较小的数字之后,然而我们分组的时候,因为取了gap值,那么较大数字排到较小数字之后的成本便大大的降低了。我们以第一组的四个数字为例:5 1 8 7 ,假设进行直接插入排序的话,那么5要到1后面要进行多次交换,但是此时我们取一个gap的值,那么此时只需要进行一次交换。
而且 gap = 1的时候就是插入排序
因为该算法的gap取值不同,则时间复杂度不是很好计算。
在源代码后面计算时间复杂度(大致时间复杂度)
稳定性该算法交换的时候,两个值交换的时候,中间肯定是有数字的啊,所以是不稳定的
希尔排序的实现

注意
gap的取值是一个我们需要注意的点,gap取太小,当需要排序的数字较多时,此时所耗费的时间还是很多,同理,当gap的值取太大的时候也不行,所以我们取gap值为数字个数的三分之一,这样就恰到好处了
注 gap的值最终要取 1,因为gap = 1的时候进行的就是直接插入排序。
// 希尔排序
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;//因为我们最终要让gap的值为1,因为gap值为1的时候最终进行的就是直接插入排序
//此时若gap>1,那么就是预处理
//gap=1时,就是直接插入排序,然后就会跳出循环
for (int i = 0; i < n - gap; i++)//注意一下,i的值时n-gap,
//否则可能会造成数组的越界
{
int end = i;
int tam = a[end + gap];//每次从i+1开始插入
while (end >= 0)
{
if (tam < a[end])
{
a[end + gap] = a[end];
end-=gap;
}
else
break;
}
a[end + gap] = tam;
}
}
}
大致时间复杂度
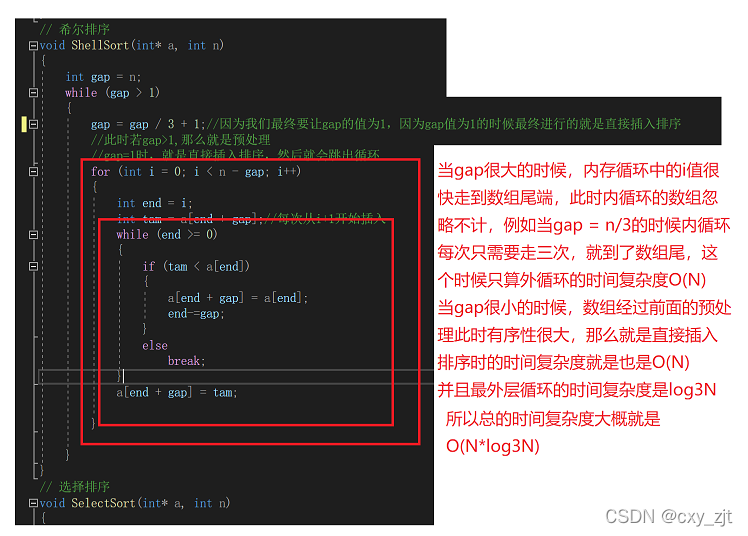
下面引用一段殷人昆老师对希尔排序的探讨

选择排序的思想+时间复杂度及稳定性

思想:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完
时间复杂度 O(N^2)
! !!!稳定性!!!!
不稳定的!!
举个例子假设有数组:
3A,3B,1,5,6,7,
我们第一次选择的时候1与3A交换,那么第一次选择后的数组变成
1,3B, 3A, 5, 6, 7,
这是不稳定的
堆排序的稳定性
堆排序的博客
不稳定的
1,一句话,数字交换或者插入之间有其他数字,那么就是不稳定的。因为堆排序是进行向下调整算法的时候,数字之间的交换中间是有数字的
2,也可以这样理解,假设有两个数字7A 7B 初始7A在7B前面,但建堆排序后7B可能在7A前面,两种理解都可以
快排的思想+时间复杂度及稳定性
第一次画动图,耐心点看完,铁子!画的不好还请见谅

下面我写了三种版本的快排,但是大致思路都是一样的
稳定性 看我下面的动图就知道,不可能稳定的
时间复杂度 见快排最后总结
1,hoare版本
思路:选择一个关键字key,然后进行排序,使得左边的值都小于key,右边的值都大于key。步骤:两个指针i,j,一个从最左边开始,一个从最右边开始,如果i指向的值小于等于key,那么i++,当i指向的值大于等于key的时候,i停止,j指向的值大于key,j–,j指向的值小于key时,再让i指向的值与j指向的值交换,直到 i = j,然后再让第一个值与此时第i个值交换,下面动图更加直观
此时[left,key-1]都是比key小的,[key+1][right]都是比key大的
排序[left,key-1] 与[key+1,right] 具体的操作和上面的的一样
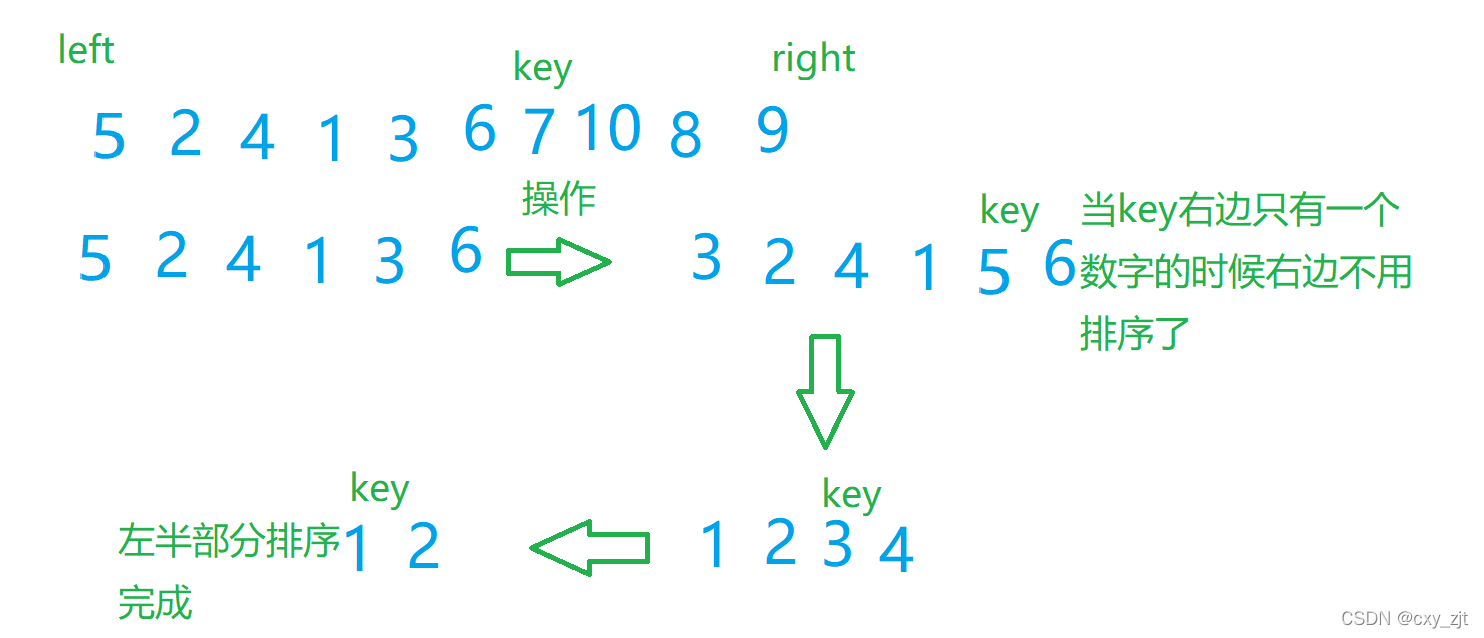
右半部分也是一样的
注意如果key选择的是左边的,一定是从最右边开始的,因为右边的值是比key大的值,左边是比key小的值,如果是从左边先开始,最终停止的值不一定是比key小的,这个时候如果让i最终指向的值与key指向的数字交换的话,此时key左边的值可能比key大,那么就不符合快速排序了
// 快速排序hoare版本
int PartSort1(int* a, int left, int right)
{
int key = a[left];
int i = left; int j = right;
while (i < j)
{
while (i<j&&a[j] >= key)
j--;
while (i<j&&a[i] <= key)//一定要加一个限制条件
//因为假设最大值是a[0]那么便有可能出现越界
//的情况
i++;
Swap(&a[i], &a[j]);
}
Swap(&a[i], &a[left]);
return i;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)//当需要排序只有一个数字的时候或者left大于right
//时直接返回
/至于为什么left还可能大于right,因为递归时从
//left,key-1
//ley+1,right
//当右半部分只剩下一个数字的时候,key+1时大于right的
return;
int key = PartSort1(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key+1, right);*/
}
2. 挖坑法
思路:大致和前面一样,不同的是先选择一个数字形成一个坑位pit

// 快速排序挖坑法
int PartSort2(int* a, int left, int right)
{
int key = a[left];
int pit = left;//坑位
int i = left; int j = right;
while (i < j)
{
while (i<j&&a[j] >= key)//内循环也应该加上i<j防止越界
j--;
if (pit != j)
{
a[pit] = a[j];
pit = j;//坑位换了
}
while (i < j && a[i] <= key)
i++;
if (pit != i)
{
a[pit] = a[i];
pit = i;
}
}
a[pit] = key;//最后一个坑位给key
return pit;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int key = PartSort2(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key+1, right);*/
}
注意:需要注意的是这个时候从左边还是右边开始走都可以
3,前后指针法
初始化两个指针:prev cur
初始值:prev指向的是序列开头,cur指向的是prev的下一个位置
思路选择一个key = 第一个数字
当cur指向的值小于key时候,prev++,cur++并且交换[++prev]指向的值和cur指向的值
当cur指向的值大于key的时候cur++ ,当cur大于right的时候跳出循环,最终交换prev指向的值与第一个key代表的值

我们这样走到话,prev与cur之间的值都是比key大的
先写一个没有优化的版本
int PartSort3(int* a, int left, int right)
{
//int key = GetMid(a, left, right);
//Swap(&a[left], &a[key]);
int key = a[left];
int prev = left, cur = left + 1;
while (cur <= right)
{
if (a[cur] <= key)
{
prev++;
Swap(&a[prev], &a[cur]);
}
cur++;
//prev与cur的关系
//cur还没遇到比key大的值时,prev紧跟着cur,一前一后
//cur遇到比key大的时候,prev和cur之间隔着一段比key的值大的区间
}
Swap(&a[prev], &a[left]);
return prev;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int key = PartSort3(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}
稍微优化一下
我们发现当++prev等于cur的时候相当于没有交换,这个时候加一个条件
int PartSort3(int* a, int left, int right)
{
//int key = GetMid(a, left, right);
//Swap(&a[left], &a[key]);
int key = a[left];
int prev = left, cur = left + 1;
while (cur <= right)
{
if (a[cur] <= key && ++prev != cur)
Swap(&a[prev], &a[cur]);
cur++;
//prev与cur的关系
//cur还没遇到比key大的值时,prev紧跟着cur,一前一后
//cur遇到比key大的时候,prev和cur之间隔着一段比key的值大的区间
}
Swap(&a[prev], &a[left]);
return prev;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
int key = PartSort3(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}
时间复杂度

I’m here!!!
快排大致就是每次分成两边,然后依次对各边进行排序
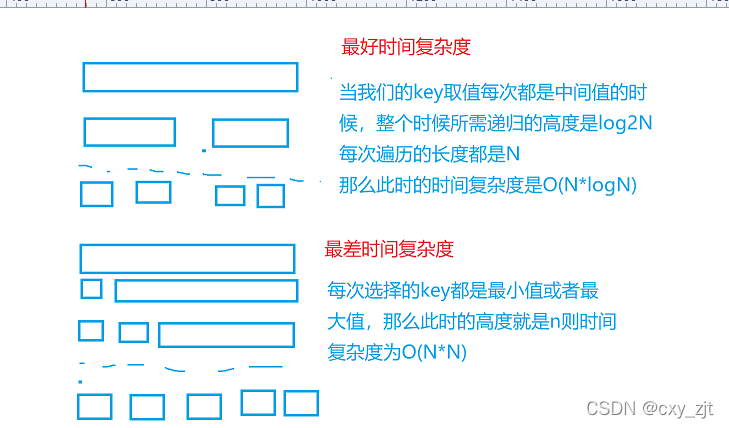
快速排序究极优化版本
从上面的时间复杂度可以看出,key值的不确定性导致了时间复杂度的不确定性,因此,我们可以对key的取值进行优化,在left,mid,以及right三者之间取中间值,这个时候保证了key不是最小值或者最大值了
int GetMid(int* a, int left, int right)
{
int mid = left + (right - left);//2//防止溢出
if ((a[left] <= a[mid] && a[left] >= a[right])||( a[left] >= a[mid] && a[left] <= a[right]))
return left;
if ((a[right] <= a[mid] && a[right] >= a[left]) || (a[right] >= a[mid] && a[right] <= a[left]))
return right;
return mid;
}
// 快速排序前后指针法
int PartSort3(int* a, int left, int right)
{
int key = GetMid(a, left, right);
Swap(&a[left], &a[key]);
int prev = left, cur = left + 1;
while (cur <= right)
{
if (a[cur] <= key && ++prev != cur)
Swap(&a[prev], &a[cur]);
cur++;
//prev与cur的关系
//cur还没遇到比key大的值时,prev紧跟着cur,一前一后
//cur遇到比key大的时候,prev和cur之间隔着一段比key的值大的区间
}
Swap(&a[prev], &a[left]);
return prev;
}
void QuickSort(int* a, int left, int right)
{
if (left >= right)
return;
/*int key = PartSort1(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key+1, right);*/
/*int key = PartSort2(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);*/
int key = PartSort3(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}
快速排序的非递归实现

思路
非递归实现,得从递归实现的时候函数的参数是什么入手,观察上面递归实现的函数可知,函数的参数每次都是需要排序的边界left以及right,因此,我们可以用栈的思想。

// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)
{
ST ret;
StackInit(&ret);
StackPush(&ret, left);//入栈
StackPush(&ret, right);//入栈
while (!StackEmpty(&ret))
{
int j = StackTop(&ret);
StackPop(&ret);
int i = StackTop(&ret);
StackPop(&ret);
int key = PartSort1(a, i, j);
if (i < key - 1)//当i的值小于key的时候说明左半部分还可以排序
{
StackPush(&ret, i);
StackPush(&ret, key-1);
}
if (key + 1 < j)//当满足这个条件的时候说明右半部分还可以排序
{
StackPush(&ret, key+1);
StackPush(&ret, j);
}
}
StackDestory(&ret);//栈的销毁
}
归并排序的思想+时间复杂度及稳定性
思想 核心思想是分治:
我们将数组分成两部分,且此时的两部分都是有序数组,然后将这两个有序的数组合并成一个有序
我用图展示一下:
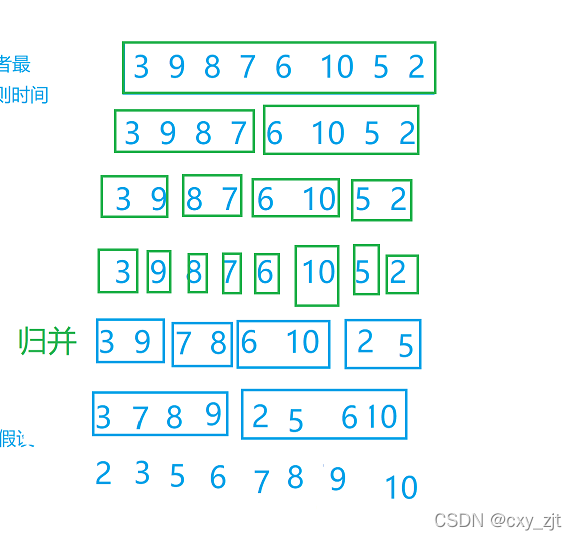
注意 两部分有序表合并成一个有序表,当其中一个有序表排完后,剩余有序表中的元素直接放到合成表后面即可。因为两边的都是有序的,当其中一个有序表全部合并完后,另一部分有序表中的值肯定是比前面合并完的有序表中的值大的
时间复杂度因为每次取值都是中间值,所以是标准的O(N*logN)
稳定性:如果左右两边值相等的时候先将左边的值排序,那么此时的算法就是稳定的,反之不稳定

归并排序的递归实现
我们每次可以拿一个数组tmp来接收需要排序的数字,最好再将tmp数组复制到原数组中。
void MergeSort(int* a, int left,int right,int*tam)
{
if (left >= right)
return;
int mid = (left + right) / 2;
MergeSort(a, left, mid, tam);
MergeSort(a, mid+1, right, tam);
int k = left;
int i = left;
int j = mid + 1;
while (i <= mid && j <= right)
{
if (a[i] < a[j])
tam[k++] = a[i++];
else
tam[k++] = a[j++];
}
while (i <= mid)
tam[k++] = a[i++];
while (j <= right)
tam[k++] = a[j++];
memcpy(a+left, tam + left, (right - left + 1) * sizeof(int));
//注意:复制的时候启示的地址是a+left
}
归并排序的非递归实现

思路 从上面的图我们可以得出,并且结合递归可以得出,归并就是先将小部分排好序,然后这两个小部分再合成一个大部分,那么我们非递归可以这样写:
分组,分成间隔为1,间隔为2,间隔为4的组
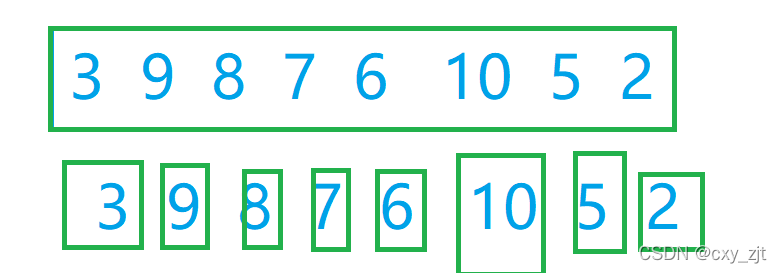
先将间隔为一的组排好序后,再排间隔为2,间隔为4
错误的代码
需要排序的数组:int arr[] = {10,2,4,1,3,9,8,6,5,7 };
// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
int gap = 1;
while (gap < n)//1 2 3 4 5 6 7 8
{
for (int i = 0;i<n;i+=gap*2)//gap = 2
{
int begin1 = i; int end1 = i + gap - 1;
int begin2 = i + gap; int end2 = i + 2 * gap - 1;
int k = begin1;
/*if (end1 >= n)
end1 = n - 1;
if (begin2 >= n)
{
begin2 = n; end2 = n - 1;
}
if (begin2 < n && end2 >= n)
end2 = n - 1;*/
printf("归并:[%d][%d] [%d] [%d]\n", begin1, end1, begin2, end2);
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
tmp[k++] = a[begin1++];
else
tmp[k++] = a[begin2++];
}
while (begin1 <= end1)
tmp[k++] = a[begin1++];
while (begin2 <= end2)
tmp[k++] = a[begin2++];
}
memcpy(a, tmp, sizeof(int) * n);
gap *= 2;
}
}
看一下输出值:
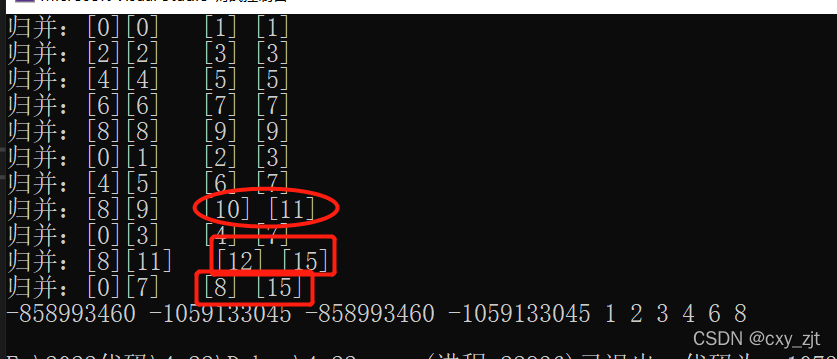
此时我们通过打印值可以发现,越界了!begin1不可能越界,但是end1,begin2以及end2都有可能越界,那么我们就应该各个进行分析:
1,当end1越界是我们将end1改成n-1
2,当begin2>=n时,此时[begin2,end2]之间的数组都越界的,此时我们改动值,改成begin2大于end2即可
3,只有end2越界,那么此时将end2改成n-1就可以了
修改后的代码只需要把我上面的那个解释取消就可以了
// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
int gap = 1;
while (gap < n)//1 2 3 4 5 6 7 8
{
for (int i = 0;i<n;i+=gap*2)//gap = 2
{
int begin1 = i; int end1 = i + gap - 1;
int begin2 = i + gap; int end2 = i + 2 * gap - 1;
int k = begin1;
if (end1 >= n)
end1 = n - 1;
if (begin2 >= n)
{
begin2 = n; end2 = n - 1;
}
if (begin2 < n && end2 >= n)
end2 = n - 1;
printf("归并:[%d][%d] [%d] [%d]\n", begin1, end1, begin2, end2);
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
tmp[k++] = a[begin1++];
else
tmp[k++] = a[begin2++];
}
while (begin1 <= end1)
tmp[k++] = a[begin1++];
while (begin2 <= end2)
tmp[k++] = a[begin2++];
}
memcpy(a, tmp, sizeof(int) * n);
gap *= 2;
}
}
输出值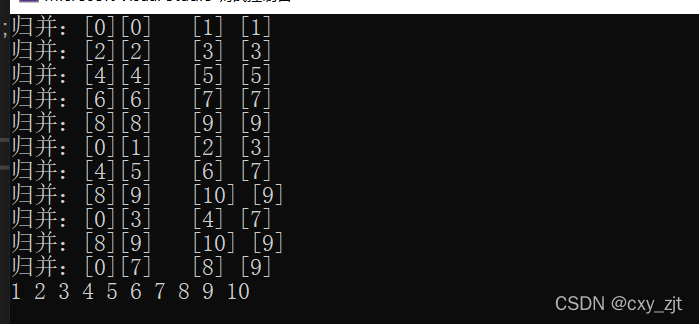
非比较排序

上面写的排序都是计数排序,都是关键字之间的比较,交换,来达到排序的目的,而非比较排序就是不用比较关键字,直接可以进行排序。
1,计数排序
思路:
假设有一个需要排序的数组为a[N],此时我们还要创造一共计数的数组count[N]来计数,遍历需要排序的数组,然后其对应的映射位置++
映射的方式有两种:
1,绝对映射
数字是多少,对应的映射位置就是多少
2,相对映射
最小数字对应的映射位置为count[0]最大数字对应的映射位置为count[max-min]
我用图表示一下

void CountSort(int* a, int n)//计数排序
{
int mi = a[0], ma = a[0];
for (int i = 0; i < n; i++)
{
if (a[i] < mi)
mi = a[i];
if (a[i] > ma)
ma = a[i];//遍历找到最大值与最小值,确定计数数组的大小
}
int range = ma - mi + 1;
int* Count = (int*)malloc(sizeof(int) * range);
assert(Count);
memset(Count, 0, sizeof(int) * range);//一定要将计数的数组全部赋值为0,否则排序会错误!!!
for (int i = 0; i < n; i++)//计数
{
Count[a[i] - mi]++;
}
int j = 0;
//将排序好的数字返回原数组
for (int i = 0; i < range; i++)
{
while (Count[i]--)//有点次数没有出现,且我们是相对映射,所以返回原来的数组时,应该加上mi最小值
{
a[j++] = i + mi;
}
}
}
由上述代码我们可以推测:
时间复杂度 O(N+range)
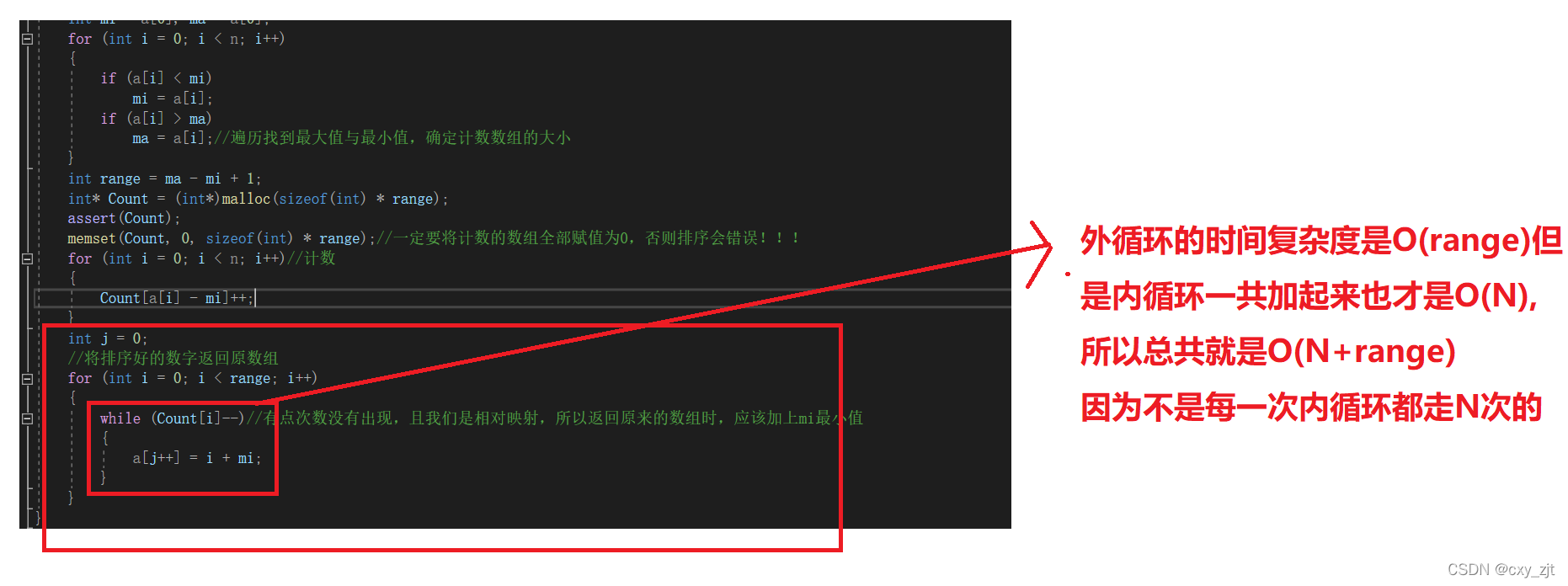
空念复杂度 O(range)
适用的场景 适用于数据较多且数据范围较集中使用
2,基数排序
基数排序有多关键字的排序和链式基数排序,下面我要讲述的是多关键字的排序。
其中又分为最高位优先法和最低位优先法
下面我介绍的是最低位优先法
假设有一串数字,都是三位数
1,遍历这一串数字,得到每个数字的个位数,根据个位数排序
2,再根据排序的顺序回收数
3,再遍历一遍这串数字,得到每个数字的十位数,再根据十位数排序
4,再根据排序的顺序回收数据
5,同理,对百位数字也是这样做
看下面动图就能看出来了
注意 无论是`分发数据还是回收数据都是先进先出
我录制的这个视频有点长hh 可以看对各位和十位的操作就可以了

因为是先进先出的,所以我们用队列来操纵
#include<iostream>
#include<assert.h>
#include<stdlib.h>
#include<queue>
#define RAdix 10//因为数字都是又0-9组成的,所以我们队列数组的范围取的是10
#define w 4//这个表示此时我们需要排序的数组中数的最大有四位数字
using namespace std;
queue <int>st[RAdix];
//279
int GetKey(int x, int u)//注意这边u是从0开始的,0表示的就是个位数
{
int t = x % 10;;
while (u--)
{
x /= 10;
t = x % 10;
}
return t;
}
void Distribute(int* a, int left, int right, int u)//u表示的数第几位数,u是从0开始的
{
for (int i = left; i < right; i++)
{
int key = GetKey(a[i], u);//得到a[i]中第u为元素
st[key].push(a[i]);
}
}
void Collect(int* a)
{
int k = 0;
for (int i = 0; i < RAdix; i++)
{
while (!st[i].empty())
{
a[k++] = st[i].front();
st[i].pop();
}
}
}
void RadixSort(int* a, int left,int right,int k)//[left,right),k表示的是一共有几位数
{
for (int i = 0; i < k; i++)
{
//分发数据
Distribute(a, left, right, i);
//回收数据
Collect(a);
}
}
void Print(int* a, int n)
{
for (int i = 0; i < n; i++)
printf("%d ", a[i]);
printf("\n");
}
int main()
{
int arr[] = { 370,350,360,500,1000,890,60,38,27 };
int sz = sizeof(arr) / sizeof(arr[0]);
RadixSort(arr, 0, sz, 4);
Print(arr, sz);
return 0;
}
常见的排序就到这了,万字长文,求赞,求关注,求三连!!!

